H C VI N CÔNG NGH B U CHÍNH VI N THÔNGỌ Ệ Ệ Ư Ễ
KHOA QU C T VÀ ĐÀO T O SAU Đ I H CỐ Ế Ạ Ạ Ọ
Báo cáo chuyên đ môn h cề ọ
X LÝ TÍN HI U S NÂNG CAOỬ Ệ Ố
N i dung báo cáo ộ
PHÉP BI N Đ I WAVELETẾ Ổ
GIÁO VIÊN H NG D N:ƯỚ Ẫ TS. Nguy n Ng c Minh.ễ ọ
NHÓM 9: Đoàn Minh Quân,
Nguy n Kim Dung,ễ
Nguy n H u Tr ng, ễ ữ ườ
Hà Th Lan Anh.ị
L P:Ớ CH10 ĐT3
Hà n i, tháng 05- 2011ộ
PH N 1Ầ
CÁC KHÁI NI M C B N VÀ T NG QUAN V LÝ THUY T WAVELETỆ Ơ Ả Ổ Ề Ế
M c dù khái ni m Wavelet đã ra đ i cách đây 10 năm, nh ng có r t ít bài báo hayặ ệ ờ ư ấ
cu n sách nào vi t v nó, và ch y u ch là các nhà toán h c vi t ra, v i r t ít số ế ề ủ ế ỉ ọ ế ớ ấ ự
tham kh o hay tr giúp, vì nó là hoàn toàn m i.ả ợ ớ
Tr c h t chúng ta c n bi t t i sao ph i bi n đ i và bi n đ i th c ch t là gì? Trongướ ế ầ ế ạ ả ế ổ ế ổ ự ấ
toán h c, phép bi n đ i lên m t tín hi u là đ có đ c các thông tin khác, mà tín hi uọ ế ổ ộ ệ ể ượ ệ
ban đ u (hay còn g i là tín hi u thô) không có. Trong ph n nghiên c u này, ta giầ ọ ệ ầ ứ ả
thuy t tín hi u mi n th i gian là tín hi u thô, còn tín hi u đã đ c bi n đ i qua cácế ệ ề ờ ệ ệ ượ ế ổ
công c toán h c là tín hi u đ c x lý. Có r t nhi u phép bi n đ i đ c áp d ng,ụ ọ ệ ượ ử ấ ề ế ổ ượ ụ
song phép bi n đ i Fourier là phép bi n đ i đ c ng d ng r ng rãi nh t.ế ổ ế ổ ượ ứ ụ ộ ấ
H u h t các tín hi u mà chúng ta đo đ c đ u là tín hi u trong mi n th i gian,và khiầ ế ệ ượ ề ệ ề ờ
chúng ta bi u di n lên đ th , thì luôn có m t tr c là th i gian, còn tr c kia là để ễ ồ ị ộ ụ ờ ụ ộ
l n.Tuy nhiên trong x lý tín hi u thì cách bi u di n đó không ph i là t i u. Vàớ ử ệ ể ễ ả ố ư
trong nhi u tr ng h p, thì thành ph n t n s l i là quan tr ng đ phân bi t các tínề ườ ợ ầ ầ ố ạ ọ ể ệ
hi u v i nhau, ng i ta dùng ph t n s đ bi u di n các thành ph n t n s có trongệ ớ ườ ổ ầ ố ể ể ễ ầ ầ ố
tín hi u.ệ
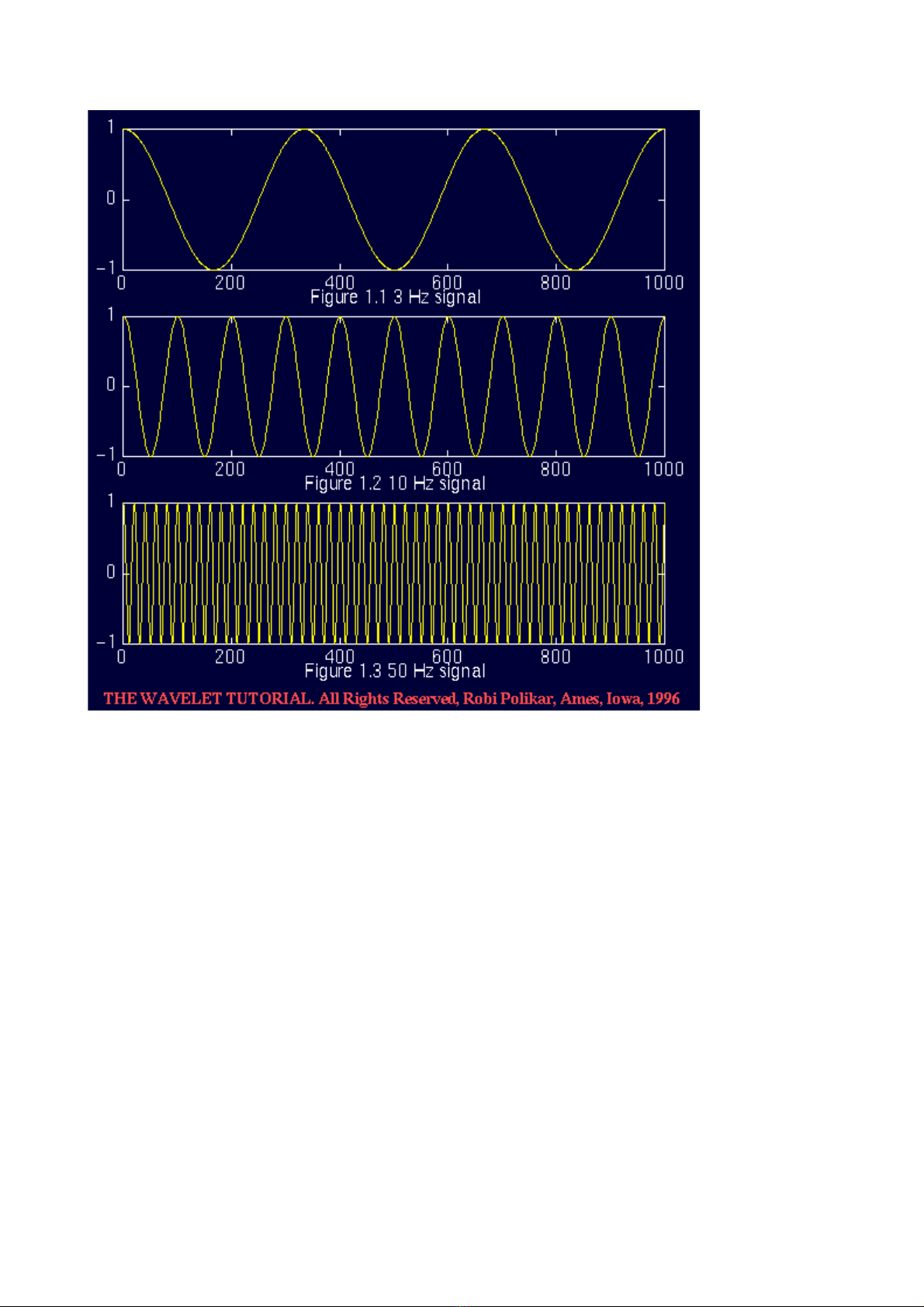
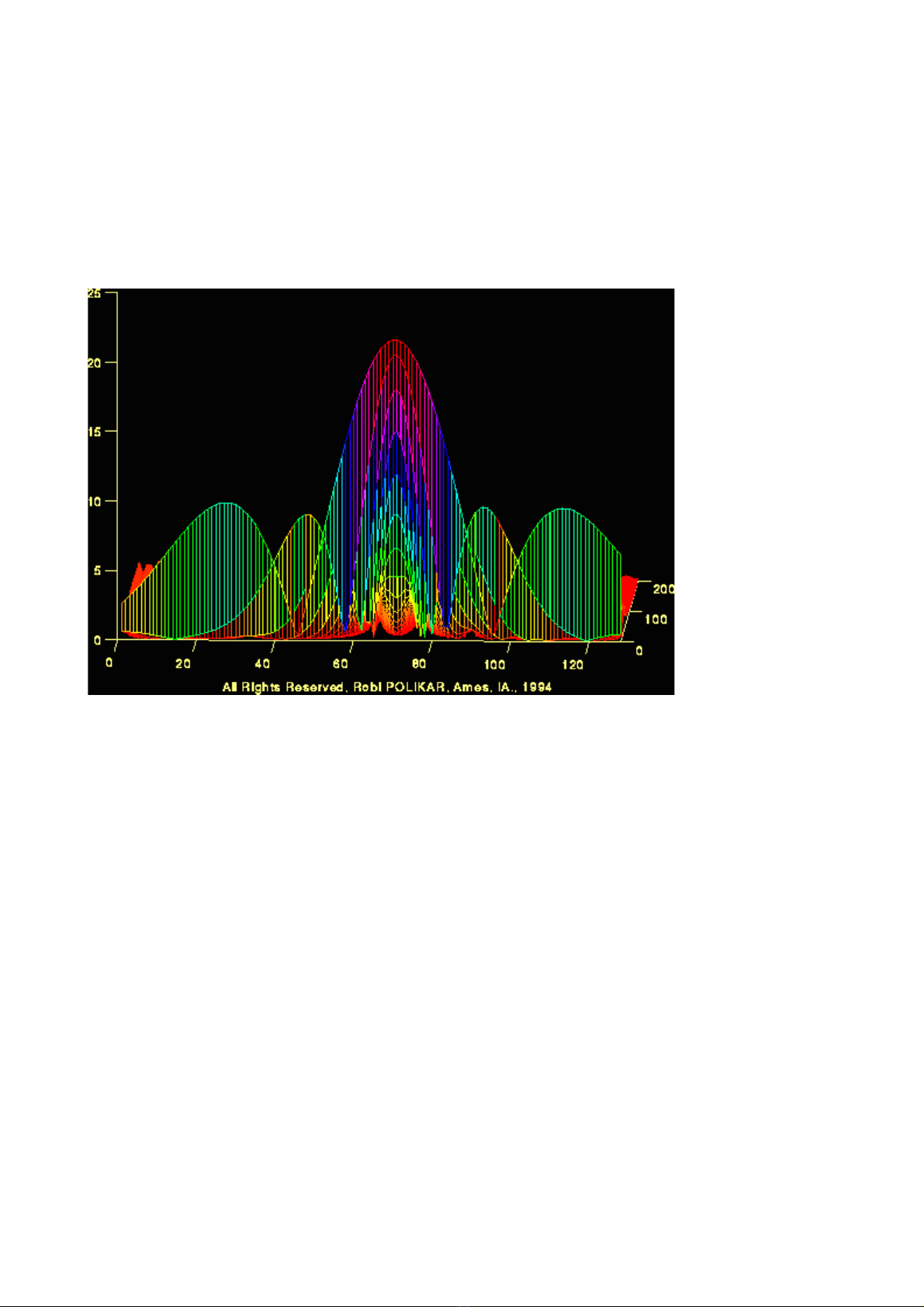
Ta hãy xem xét hình v d i đây bi u di n 3 tín hi u t ng ng 3 t n s khác nhauẽ ướ ể ễ ệ ươ ứ ầ ố
V y làm th nào đ đo đ c t n s và làm th nào đ tìm ra các thành ph n t n sậ ế ể ượ ầ ố ế ể ầ ầ ố
trong tín hi u? Câu tr l i chính là phép bi n đ i Fourier. Phép bi n đ i FOURIERệ ả ờ ế ổ ế ổ
cho ta bi t đ l n tín hi u trong m i thành ph n t n s .ế ộ ớ ệ ỗ ầ ầ ố
Xác đ nh thành ph n t n s có ý nghĩa quan tr ng trong k thu t, ví d trong y h c,ị ầ ầ ố ọ ỹ ậ ụ ọ
d a vào thành ph n t n s đo đ c trong nh p tim, mà ta bi t đ c ng i đó có kh eự ầ ầ ố ượ ị ế ượ ườ ỏ
hay không?
Tuy nhiên có r t nhi u phép bi n đ i đ c áp d ng trong k thu t và toán h c, nhấ ề ế ổ ượ ụ ỹ ậ ọ ư
bi n đ i Hilbert, bi n đ i Fourier th i gian ng n, phân b Wigner , bi n đ i Radon,ế ổ ế ổ ờ ắ ố ế ổ
… M i phép bi n đ i đ u có nh ng vùng ng d ng riêng v i nh ng u nh c đi mọ ế ổ ề ữ ứ ụ ớ ữ ư ượ ể
khác nhau. Phép bi n đ i Wavelet mà ta đang nghiên c u cũng không là ngo i l .ế ổ ứ ạ ệ
Đ bi t s c n thi t c a phép bi n đ i Wavelet, chúng ta hãy xem qua phép bi n đ iể ế ự ầ ế ủ ế ổ ế ổ
Fourier. FT là phép bi n đ i 2 chi u gi a tín hi u thô và tín hi u x lý. Ta s khôngế ổ ề ữ ệ ệ ử ẽ
th bi t đ c th i gian trong tín hi u x lí, và cũng không th bi t đ c t n s trongể ế ượ ờ ệ ử ể ế ượ ầ ố
mi n tín hi u thô. V y m t câu h i đ t ra là ta có c n bi t đ n c t n s và c th iề ệ ậ ộ ỏ ặ ầ ế ế ả ầ ố ả ờ
gian cùng m t lúc không? N u đ i v i các quá trình d ng thì vi c này là không c nộ ế ố ớ ừ ệ ầ
thi t, vì quá trình d ng, thành ph n t n s là không thay đ i theo th i gian. Ta hãyế ở ừ ầ ầ ố ổ ờ
xem ví d d i đây:ụ ướ
Đây là bi n đ i Fourier c a nó:ế ổ ủ
Khác v i tín hi u hình 1.5, ta xét tín hi u khác không d ng đ c minh h a d iớ ệ ở ệ ừ ượ ọ ướ
đây:
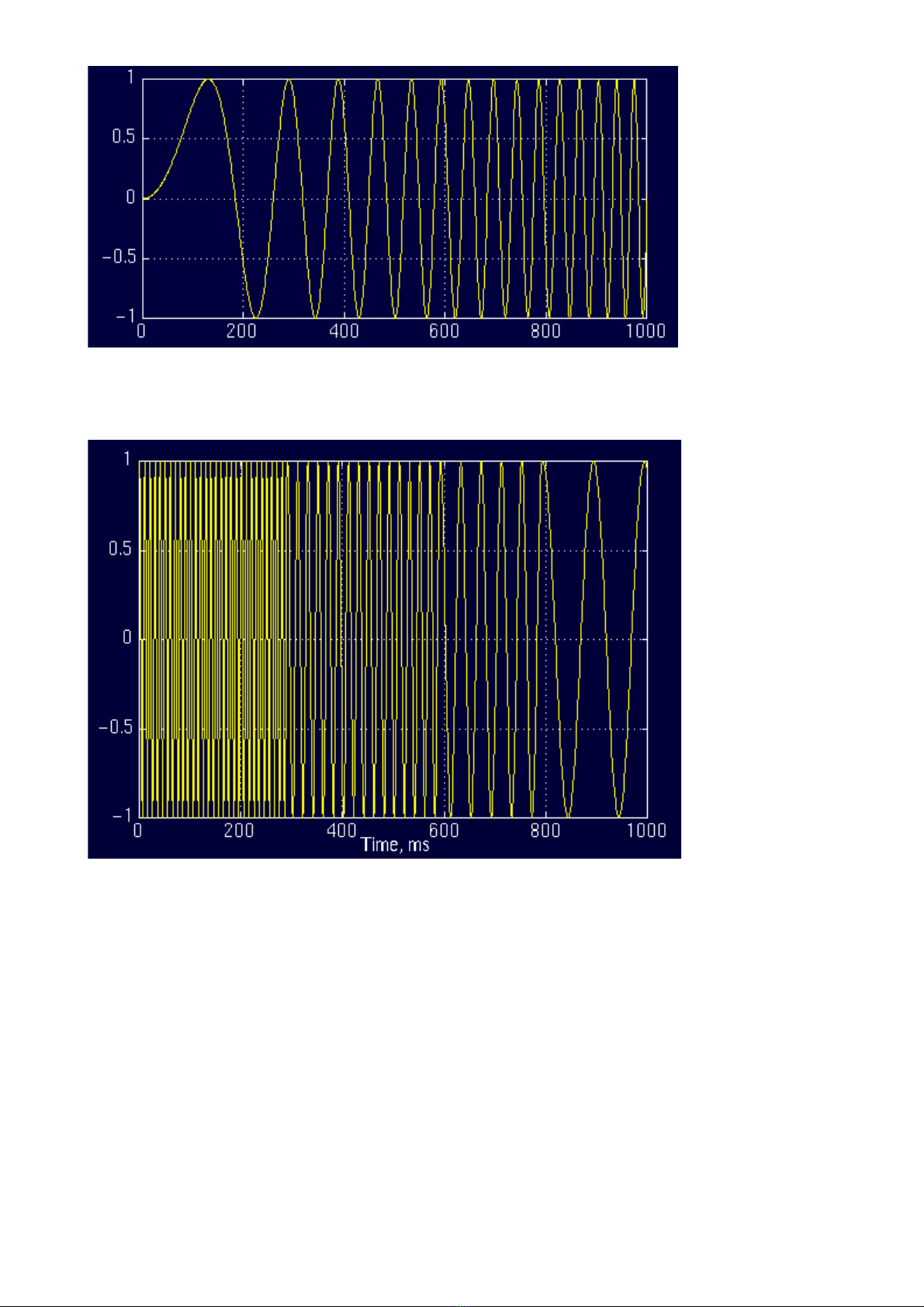
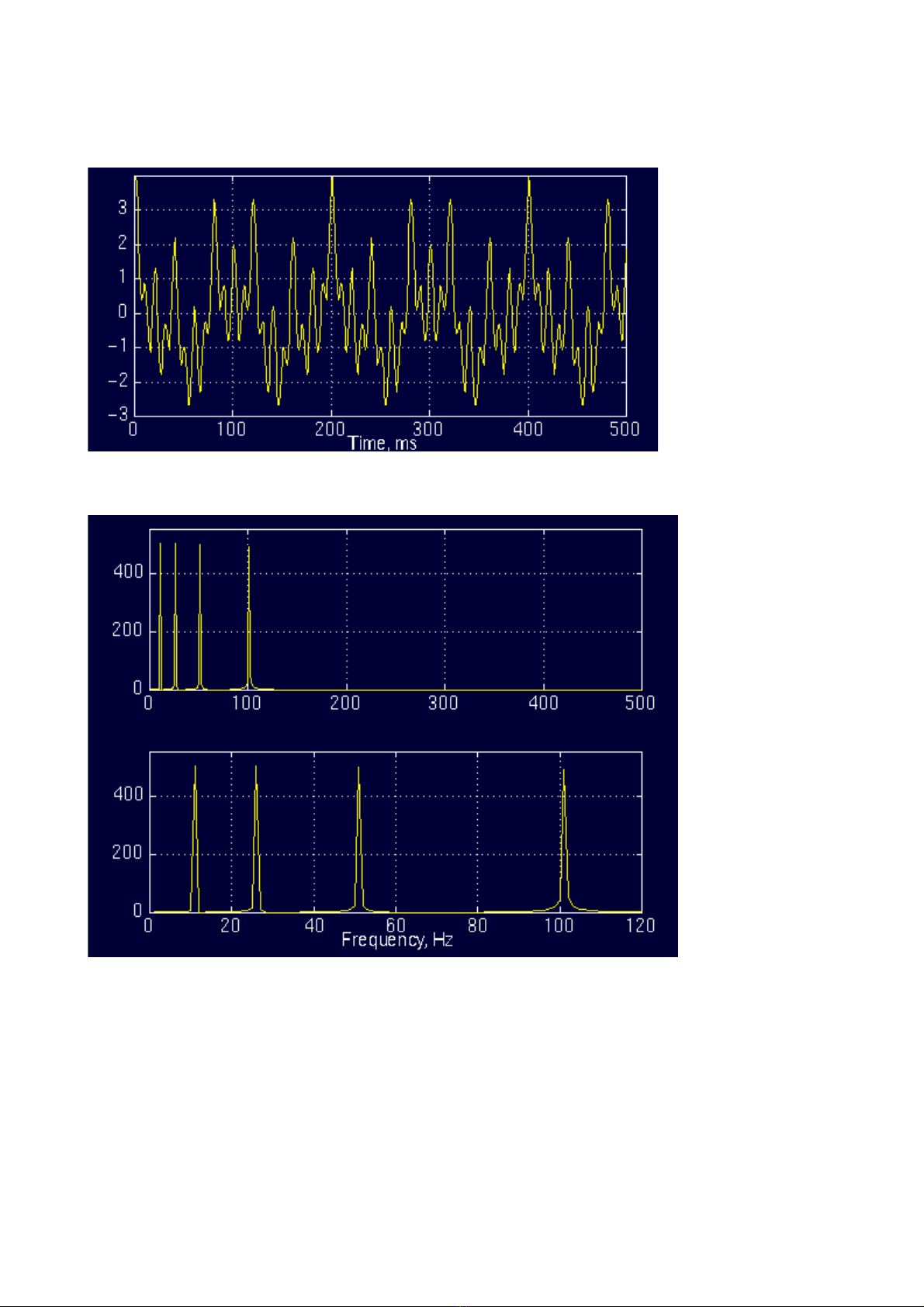
L i xét ti p m t ví d khác có 4 thành ph n t n s 4 kho ng th i gian khác nhau,ạ ế ộ ụ ầ ầ ố ở ả ờ
do đó đây cũng không ph i là tín hi u d ng.ả ệ ừ
Và bi n đ i FT c a nó có d ng:ế ổ ủ ạ