Tuyển tập Hội nghị Khoa học thường niên năm 2016. ISBN: 978-604-82-1980-2
169
TRẬT TỰ TỪ TRONG MẠNG TAM GIÁC PHẢN SẮT TỪ
HEISENBERG VỚI SPIN S = 1
Phạm Thị Thanh Nga
Trường Đại học Thủy lợi
1. GIỚI THIỆU CHUNG
Một vấn đề được quan tâm nghiên cứu rất
nhiều cả về lý thuyết lẫn thực nghiệm hiện
nay là các tính chất từ của hệ mô men từ
Heisenberg phản sắt từ trên mạng tam giác
[9]. Một mặt, mạng tam giác phản sắt từ là
mạng Bravais duy nhất có tính chất vấp từ
tương tác – một thách thức thú vị cho các nhà
vật lý lý thuyết. Mặt khác, các nhà vật lý thực
nghiệm đã phát hiệu nhiều họ vật liệu từ có
cấu trúc tam giác với nhiều tính chất chưa
được giải thích thấu đáo [2]. Mô hình
Heisenberg phản sắt từ biểu diễn qua các toán
tử spin ở nút i của mạng tinh thể có dạng:
ij i j ij
ij
H J S .S (J 0 )
(1)
Các toán tử spin không phải là toán tử
chính tắc bởi chúng thỏa mãn giao hoán tử
sau thay vì là các hệ thức giao hoán cho
boson hay phản giao hoán cho fermion:

i ij
j
S ,S i S ( , , =x,y,z)
(2)
vì vậy không áp dụng được các kỹ thuật lý
thuyết hệ nhiều hạt thông thường. Để khắc
phục khó khăn này người ta đã thay toán tử
spin bằng các toán tử chính tắc boson hoặc
các fermion [1]. Tuy nhiên, không gian Fock
của các toán tử đều lớn hơn không gian
Hilbert của toán tử spin nên việc loại bỏ các
trạng thái phi vật lý thường phải tính một
cách gần đúng bằng cách đưa vào điều kiện
ràng buộc chỉ có một spin trên một nút. Năm
1988, Popov-Fedotov đã đề xuất một phương
pháp mới có thể loại trừ các trạng thái phi vật
lý (không có spin nào hoặc có hơn một spin
trên một nút) một cách chính xác trên mỗi nút
bằng cách đưa vào thế hóa học ảo
phụ
thuộc spin [6] cho hai trường hợp S = ½ và
S = 1. Tuy nhiên, các tính toán cụ thể chỉ
được triển khai với trường hợp S = ½ [3, 4, 7]
cho mạng hình vuông và [8] cho mạng tam
giác. Trong thực tế người ta phát hiện nhiều
vật liệu mạng tam giác có spin S = 1 [5, 11].
Trong công trình gần đây, chúng tôi đã triển
khai các tính toán ban đầu cho S = 1[10]
nhưng mới dừng lại ở biểu thức của năng
lượng tự do trong gần đúng một vòng và biểu
thức cho độ từ hoá phân mạng ở gần đúng
trường trung bình. Trong báo cáo này chúng tôi
phát triển các kết quả của [10] và áp dụng cho
mạng tam giác.
2. PHƯƠNG PHÁP NGHIÊN CỨU
Chúng tôi sẽ nghiên cứu hệ spin S = 1 trên
mạng tam giác (Hình 1) với Hamiltonian (1)
trong gần đúng tương tác giữa các nút lân cận
gần nhất bằng J.
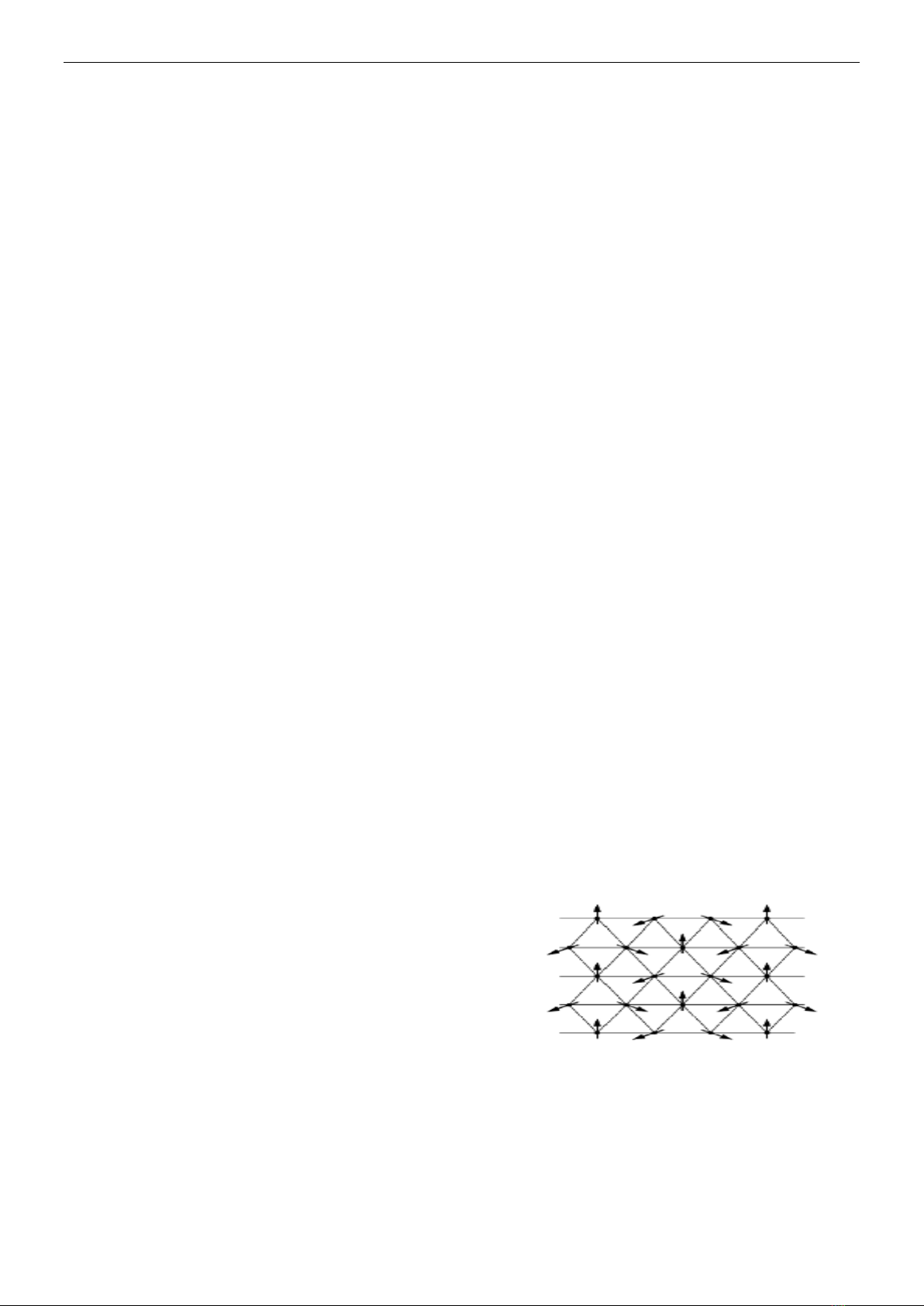
Hình 1. Trạng thái cơ bản cổ điển
là cấu trúc spin 120o
Sử dụng phương pháp tích phân phiếm
hàm Popov-Fedotov khi biểu diễn các toán tử
spin qua các toán tử fermion
i i
a ,a
với
= 1, 2, 3:
Tuyển tập Hội nghị Khoa học thường niên năm 2016. ISBN: 978-604-82-1980-2
170

i i i
S a a
(3)
trong đó

là ma trận 3x3 biểu diễn các spin
S = 1 [4]. Để loại bỏ các trạng thái phi vật lý,
Popov-Fedotov đưa vào toán tử chiếu:
i
Ni
ˆ
P N.e
(4)
trong đó:
i / 3
và
N i / 3
cho
S = 1. Chúng tôi tiến hành tính toán theo các
bước sau đây, sau khi kế thừa các kết quả
nghiên cứu trước đây của chúng tôi [10, 11]:
i) Biến đổi về hệ trục tọa độ định xứ với
trục lượng tử spin Oz trùng với hướng từ hóa
cổ điển của mỗi nút mạng.
ii) Biểu diễn tổng thống kê dưới dạng tích
phân phiếm hàm trong các trạng thái kết hợp
của các biến Grassman ứng với các toán tử
sinh hủy fermion
i i
a ,a
.
iii) Dùng biến đổi Hubbard-Stratonovich
đưa vào các trường phụ boson. Mỗi trường
phụ boson tách ra phần trường trung bình và
phần thăng giáng.
iv) Lấy tích phân dạng Gauss với các
trường fermion và tính đóng góp của thăng
giáng trong gần đúng một vòng.
v)yTổng các biến theo các tần số
Matsubara cải biến có thể tính bằng định lý
thặng dư trong lý thuyết hàm biến phức.
Các tính toán không quá phức tạp, tuy
nhiên khá cồng kềnh, vì vậy chi tiết sẽ được
công bố trong một công trình khác.
3. KẾT QUẢ NGHIÊN CỨU
3.1. Các kết quả giải tích
i) Năng lượng tự do của hệ:
MF zz
F F F F
(5)
trong đó:
2
MF o o
N N
F 3Jm ln( 2cosh3 Jm 1)
2 (6)
zz o
p
1
F ln A
2 (7)
o
p
p
m
1
F ln sh ln sh
2 2 (8)
2 zz
zz
2
o 2
W ( p )K
A 1 X p K
X( p ) 3J
(9)
zz 2 2
2 o o
1
K 4 3m 4 3m
3
(10)
x
x y
x x x
y y
p3
X( p ) J cos p 2cos cos p
2 2
Y( p ) 2X ( p )
(11)
p p 3 p 3
W( p ) i4J sin cos p sin p
2 4 4
và năng lượng magnon:
o
1/ 2
( p ) 3Jm ( p ),
X( p ) Y( p )
( p ) 1 1
3J 3J
(12)
với mo thỏa mãn các phương trình:
o o
m 3 Jm
(13)
2 sinh x
x
1 2cosh x
(14)
ii) Độ từ hoá tự phát trên mỗi nút:
zz
0
m m m m
(15)
zz
p o
1 B
m
2 A
(16)



o
p
p
oo
p
1 ( p)
m coth 3J m ( p)
2 2
X( p) Y( p )
1
1 ( p) 6J
coth
2 2 ( p)
3J m
1
coth 1 3J m
2 2
(17)
với:
2 zz 2 zz
2 2
o
W (p) dK W K
B X(p)
X( p) 3J d
m 3J X( p)
(18)
zz
2
0
zz
2
K
m
1 3J K
(19)
iii) Một số hệ quả từ kết quả giải tích:
+ Nhiệt độ chuyển pha ở gần đúng trường
trung bình:
- Ràng buộc gần đúng (
0
):
Co
T 3J / 2
- Ràng buộc chính xác (
i / 3
):
C
T 2J
Tuyển tập Hội nghị Khoa học thường niên năm 2016. ISBN: 978-604-82-1980-2
171
Tức là:
C Co
T / T 4 / 3
và nhỏ hơn trường hợp
S = ½ với
C Co
T / T 2
[3]
+ Ở T = 0K: Năng lượng trạng thái cơ bản
và độ từ hoá tự phát trên mỗi phân mạng
trùng với kết quả khi điều kiện ràng buộc lấy
gần đúng.
3.2. Kết quả tính số
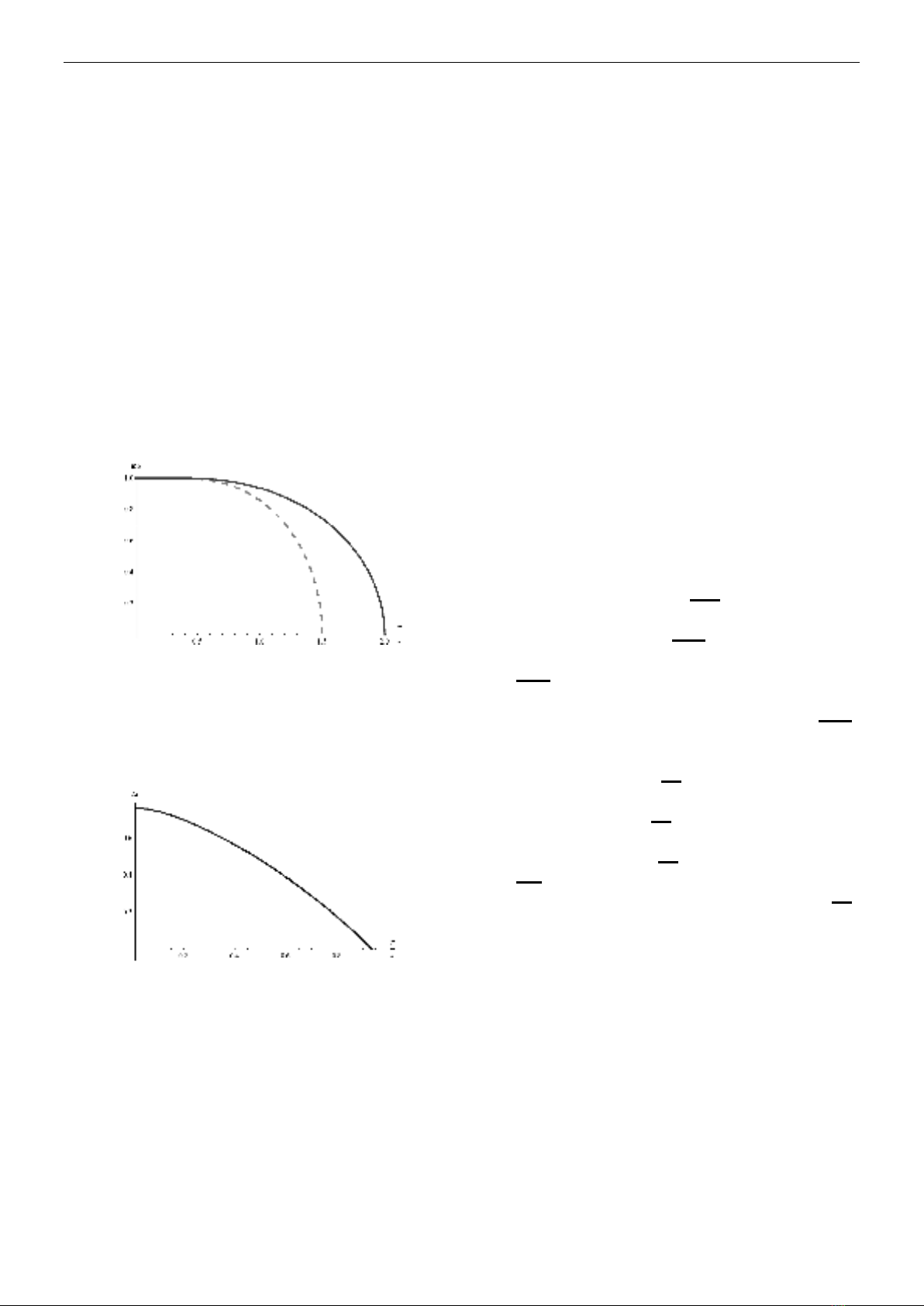
i) Đồ thị sự phụ thuộc nhiệt độ của độ từ hóa
(Hình 2) cho mạng tam giác với spin
S = 1 khi điều kiện ràng buộc lấy chính xác
(
i / 3
- đường liền nét) và so sánh với
độ từ hóa khi điều kiện ràng buộc lấy trung
bình (
o o
0 : m Tanh 3 Jm / 2
- đường
đứt nét).
Hình 2
ii) Đồ thị sự phụ thuộc nhiệt độ của độ từ
hóa tự phát trên mỗi nút (Hình 3) cho mạng
tam giác với spin S = 1 khi điều kiện ràng
buộc lấy chính xác
i / 3
.
Hình 3
4. KẾT LUẬN
i) Đã thu được biểu thức giải tích tường
minh cho năng lượng tự do và độ từ hoá tự
phát trên mỗi phân mạng.
ii) Từ các kết quả giải tích suy ra nhiệt độ
chuyển pha thuận từ - phản sắt từ ở gần đúng
trường trung bình sẽ lớn hơn so với khi ràng
buộc tính gần đúng, nhưng nhỏ hơn so với
khi S = 1/2. Năng lượng trạng thái cơ bản và
độ từ hoá tự phát ở T = 0K trùng với kết quả
khi ràng buộc lấy gần đúng.
iii) Khảo sát số cho thấy ở T 0K, các kết
quả khi tính chính xác điều kiện ràng buộc
khác biệt đáng kể so với khi ràng buộc tính
gần đúng.
iv) Các tính toán trong báo cáo có thể mở
rộng để khảo sát các vật liệu từ có cấu trúc
mạng khác. Đây là các vấn đề dành cho các
nghiên cứu khác [12].
LỜI CẢM ƠN
Xin cảm ơn sự hỗ trợ của Quỹ Nghiên cứu
Khoa học cơ bản Quốc gia Nafosted với HĐ
số 103.01-2014.23. Tác giả cũng xin cảm ơn
GS. Nguyễn Toàn Thắng và PGS. Hoàng Anh
Tuấn đã có những buổi trao đổi rất bổ ích.
5. TÀI LIỆU THAM KHẢO
[1] Aurbach, A. (1994), Interacting electrons
and quantum magnetism, Springer Verlag.
[2] Collins, M. F. and Petrenko, O. A.
(1997), Can. J. Phys. 605.
[3] Dillenschneider, R. and Richert, J.
(2006), Phys. Rev. B73, 024409.
[4] Kiselev, N. (2006), Int. J. Mod. Phys.
B20, 381.
[5] Karolak, M., Edelmann, M. and
Sangiovanni, G. (2015), Phys. Rev. B91,
075108.
[6] Popov, V. N. and Fedotov, S. A. (1988),
Sov. Phys. JETP, 67, 535.
[7] P.T.T.Nga and N.T.Thang (2014),
Comm. in Phys. 22 193.
[8] P.T.T.Nga and N.T.Thang (2012),
Comm. in Phys. 22, 33, Comm. in Phys.
22 383 (2012) Erratum.
[9] Starykh, A. (2015), Rep. Prog. Phys., 78,
052502.
[10] P.T.T.Nga and N.T.Thang , Báo cáo tại HN
VLLT 40th tại Đà lạt, 27 - 30 July 2015.
[11] P.T.T.Nga, P.T.T.Trang and N.T.Thang,
“The spatially anisotropic triangular
lattice antiferromagnet:Popov-Fedotov
method”, Báo cáo tại HN VLLT 41th, tại
Nha Trang, 1- 4 August 2016.
[12] P.T.T.Nga, T.T.Thuy and N.T.Thang
“Magnetic properties of
antiferromagnetic Heisenberg spin-1
systems in an interpolating square–
triangular lattice”, Báo cáo tại Hội thảo
Quốc tế về Các vấn đề hàng đầu về Khoa
học Vật liệu (3rd-FMS 2016, Hà Nội, 28-
30/9/2016)./.