
Tuyển tập Hội nghị Khoa học thường niên năm 2015. ISBN : 978-604-82-1710-5
91
HIỆU ỨNG ÂM - ĐIỆN VÀ ÂM - ĐIỆN - TỪ TRONG
DÂY LƯỢNG TỬ HÌNH TRỤ VỚI HỐ THẾ CAO VÔ HẠN
Nguyễn Văn Nghĩa1 và Nguyễn Quang Báu2
1Đại học Thủy lợi, email: nghia_nvl@tlu.edu.vn
2Đại học Khoa học Tự nhiên Hà Nội, email: nguyenquangbau@yahoo.com
1. Giíi thiÖu chung
Vài thập niên gần đây, ngành vật lí bán dẫn
đã đạt được nhiều tiến bộ và thành công. Sự
tiến bộ của vật lí bán dẫn được đặc trưng bởi
sự chuyển hướng nghiên cứu chính từ các khối
tinh thể sang các màng mỏng và các cấu trúc
thấp chiều như hố lượng tử, các siêu mạng, các
dây lượng tử và chấm lượng tử… Khi nghiên
cứu các tính chất vật lí trong các cấu trúc bán
dẫn thấp chiều các nhà khoa học đã chú ý
nhiều đến sự ảnh hưởng của sóng âm đến các
tính chất của vật liệu thấp chiều. Như chúng ta
đã biết, sự lan truyền của phonon âm (sóng âm)
ngoài vào bán dẫn đã làm gia tăng sự chuyển
năng lượng và xung lượng cho các điện tử dẫn
trong bán dẫn và làm xuất hiện một dòng thông
thường gọi là dòng âm - điện (AE). Điều này
dẫn đến sự xuất hiện một hiệu ứng AE dọc, tức
là có một dòng điện không đổi chạy dọc trong
mẫu (dây lượng tử) ngược chiều với sóng âm.
Khi mẫu bán dẫn đặt trong từ trường ngoài
(EMF) vuông góc với phương truyền sóng âm
thì trong mẫu này xuất hiện một hiệu ứng khác
gọi là hiệu ứng âm – điện – từ (AME). Bản
chất của hiệu ứng AME là do sự tồn tại của các
dòng từng phần được tạo ra bởi các nhóm năng
lượng khác nhau của các điện tử, khi dòng AE
toàn phần trong mẫu bán dẫn bằng không. Gần
đây đã có nhiều nghiên cứu lý thuyết về hiệu
ứng AE trong bán dẫn khối [1], trong siêu
mạng pha tạp [2] và hiệu ứng AME cũng được
nghiên cứu trong hố lượng tử [3] cho cả vùng
từ trường yếu và vùng từ trường mạnh.
Trong bài viết này chúng tôi nghiên cứu về
hiệu ứng AE và AME trong dây lượng hình
trụ với hố thế cao vô hạn (CQWIP) bằng
phương pháp phương trình động lượng tử.
Xuất phát từ Hamiltonian của hệ, chúng tôi
xây dựng phương trình động lượng tử từ
phương trình chuyển động Heisenberg và
tính toán cho CQWIP. Chúng tôi tính toán
giải tích và nhận được biểu thức giải tích cho
dòng AE và trường AME trong CQWIP khi
có EMF. Kết quả lý thuyết của dòng AE và
trường AME được đánh giá bằng số, vẽ đồ
thị và thảo luận cho CQWIP AlGaAs/GaAs.
Cuối cùng kết quả được so sánh để thấy rõ sự
khác biệt so với bán dẫn khối [1], siêu mạng
[2] và hố lượng tử [3].
2. Ph-¬ng ph¸p nghiªn cøu
Trong quá trình nghiên cứu về hiệu ứng
AE và AME trong CQWIP chúng tôi sử dụng
phương pháp phương trình động lượng tử.
3. KÕt qu¶ nghiªn cøu
a) Hamiltonian mô tả tương tác của hệ
Xét dây lượng tử CQWIP, trong đó giả
thiết rằng điện tử có thể chuyển động tự do
theo phương z và bị giam cầm theo hai
phương còn lại x và y. Hàm riêng và phổ năng
lượng của điện tử trong CQWIP đã nhận
được từ việc giải phương trình Schrodinger
cho một điện tử chuyển động trong dây đó
tương ứng là:
)r(z
p
iexpinexp
LR
)r( l,n
z
p,l,n
2
1
(1)
2
22
22
22 mR
B
m
p
pl,n
z
zl,n
, (2)

Tuyển tập Hội nghị Khoa học thường niên năm 2015. ISBN : 978-604-82-1710-5
92
trong đó m là khối lượng hiệu dụng của điện
tử; l =1,2,3,...là số lượng tử xuyên tâm,
n = 0,±1,±2,... là số lượng tử góc phương vị,
L là chiều dài và R là bán kính của CQWIP,
pz là véc tơ động lượng của điện tử dọc theo
trục z và
)B(J/R/rBJ)r( l,nnl,nnl,n 1
là hàm
xuyên tâm của điện tử, với Bn,l là nghiệm thứ
l của hàm Bessel cấp n.
Giả sử rằng sóng âm ngoài có tần số ωq
truyền dọc CQWIP và xét trường hợp thực tế
từ điểm thực nghiệm ở nhiệt độ thấp, khi ωq/η
= νs|q|/η << 1 và qd >>1, ở đây η là tần số dao
động của điện tử, vs vận tốc sóng âm, q là số
sóng âm ngoài và d là quãng đường tự do trung
bình của điện tử. Vì vậy, chúng tôi có
Hamiltonian mô tả tương tác của hệ điện tử với
phonon âm trong và ngoài trong CQWIP trong
sự lượng tử hóa lần thứ hai như sau:
n,l z n,l,p kk
n,l,p zk
z
n,l,p k
z
n',l' '
n,l kk
n',l',p k k
n',l',p
zz
n,l,n',l',k
n',l'
q ' q q
n,l n',l',p q n',l',p
zz
n,l,n',l',q
H ( p )a a b b
I C a a b b
C U a a b exp( i t )
(3)
ở đây
SLvkC s
k
2/
là thừa số tương tác
giữa điện tử – phonon âm trong, ρ là mật độ
khối lượng của bán dẫn, Λ là hằng số thế dạng,
S là thiết diện của CQWIP,
q
C
là thừa số tương
tác điện tử - phonon âm ngoài,
z
p,l,n
a
(
z
p,l,n
a
) là
toán tử sinh (hủy) điện tử,
k
b
(
k
b
) là toán tử
sinh (hủy) phonon âm trong,
q
b
là toán tử hủy
phonon âm ngoài,
'l,'nl,n
U
là yếu tố ma trận của
toán tử U và
'l,'nl,n
I
là thừa số dạng của điện tử.
b) Biểu thức giải tích cho dòng AE
Để thiết lập phương trình động lượng tử
cho điện tử khi sự có mặt của sóng siêu âm
và EMF, chúng tôi sử dụng phương trình
chuyển động cho giá trị trung bình thống kê
đối với điện tử
t
z
p,l,n
z
p,l,n H),t(ft/)t(fi
.
Sử dụng Hamiltonian từ phương trình (3) và
thực hiện các tính toán phức tạp, nhận được
biểu thức giải tích cho dòng AE trong
CQWIP như sau:
4
25
3
25
2
236
23242
2
00
2
3
1
3
2
35
3
2
00
8
4
TeTe
eU
FSv
mvfe
TeTe
eI
mv
mfe
j
//
'l,'n,l,n
Q'l,'nl,n
s
/
/
ql
'l,'n,l,n
Q'l,'nl,n
qs
(4)
ở đây
24 2222 /)mR/()BB( ql,n'l,'n
;
2/
k
;
)m/(BQ l,nF 2
22
;
)(K)(K)(K)(KBT
012311 33
;
)(K)(K)(K)(KBT
012322 33
;
)(K)(K)(K)(KT
2
1
2
1
2
3
2
53 33
)(K)(K)(K)(KT
2
1
2
1
2
3
2
54 33
3
12
/mB
;
3
22
/mB
,
với β = 1/kBT, kB là hằng số Boltzmann, T là
nhiệt độ của hệ, εF là năng lượng Fermi và
Kn(x) là hàm Bessel loại hai.
c) Biểu thức giải tích cho trường AME
Xuất phát từ phương trình cho mật độ dòng
AME toàn phần trong CQWIP khi có EMF
jijijjiji)(Ej
, (5)
ở đây αij là tenxơ độ dẫn điện, βij và ηij là các
tenxơ độ dẫn âm.
Chúng tôi xét trường hợp sóng âm truyền
dọc phương x, EMF song song với phương z
và cũng giả định rằng mẫu bán dẫn để hở
theo các hướng, vì vậy ji = 0. Do đó, chúng
tôi tính toán giải tích và thu được biểu thức
giải tích cho trường AME xuất hiện dọc theo
phương y trong CQWIP như sau
'l,l,n,n l
n
l
n
AME MAMAM ]YY[A
me
E
21
21
2
024
(6)
với
3
22
n',l'
B2
n,l
4n,l,n',l'
ks
33
12
3
2
4 3 2 2
sq n',l' 2
n,l
n,l,n',l'
22
12
q
e k T
AI
4 v LS
( ) ( )
8e v U
FS
q{ (q 2m ) (q 2m )}
Tuyển tập Hội nghị Khoa học thường niên năm 2015. ISBN : 978-604-82-1710-5
93
22
222
1
1
1
)]xcos()x(si)xsin()x(ci)[sin(
Y)]sin(cosA)cos(sin[Y l
n
2
2sinM)sinA(Y l
n
)]x(cos)x()[sinx(si)x(ci
)xcos()xsin()]x(si)x(ci[Y
22
22
]McosY))x(si)x(ci[()sinA(
]cosY))x(si)x(ci[(sin
)sin()]xsin()x(si)xcos()x(ci[M
l
n22
2
1
222
2222
222
1
)]x(sin)x(si)x(cos)x(ci[cossin
)sin(YM
22222
2
2
2
12
2
)]sin()()cos()([ xxsixxciM
)A(m k
l
n
'l,l 'n,n
2
1
;
l
n
mA2
;
)A(m k
l
n
'l,l 'n,n
2
2
;
'l
n
l
n
'l,l 'n,n AA
;
qk
'l,l 'n,n
1
;
qk
'l,l 'n,n
2
;
1
12
1212 1
2k
kk
)!k)(k( x)(
)x(si
;
c
BTk
0
;
1
2
22 1
k
kk
)!k(k x)(
)xln()x(ci
;
c
x
0
1
.
d) Khảo sát số và thảo luận
Để khảo sát rõ hơn sự phụ thuộc của dòng
AE và trường AME trong CQWIP vào các
thông số nhiệt độ của hệ, bán kính của CQWIP
và từ trường ngoài, trong phần này chúng tôi sẽ
tính toán, vẽ đồ thị và thảo luận các kết quả
trên CQWIP AlGaAs/GaAs. Các tham số được
sử dụng trong các tính toán số như [2,3]:
τ0 = 10-12s,
= 104Wm-2, ρ = 5320kgm-3,
vl = 2×103ms-1, vt = 18×102ms-1, vs = 5370ms−1,
Λ =13,5eV, ωq = 1,46×109 s−1, e = 2,07e0,
m = 0,067me và n=0,±1; n’=0,±1; l=1; l’=1.
Hình 1. Sự phụ thuộc của dòng AE vào
bán kính CQWIP và nhiệt độ của hệ.
Hình 1 biểu diễn sự phụ thuộc của dòng AE
vào bán kính của CQWIP và nhiệt độ của hệ
ứng với chiều dài CQWIP L = 90 nm. Từ đồ
thị ta thấy, dòng AE đạt giá trị cực đại tại nhiệt
độ T = 30K và bán kính R = 30 nm. Do vậy,
dòng AE trong CQWIP phụ thuộc phi tuyến
vào bán kính của dây này và nhiệt độ của hệ.
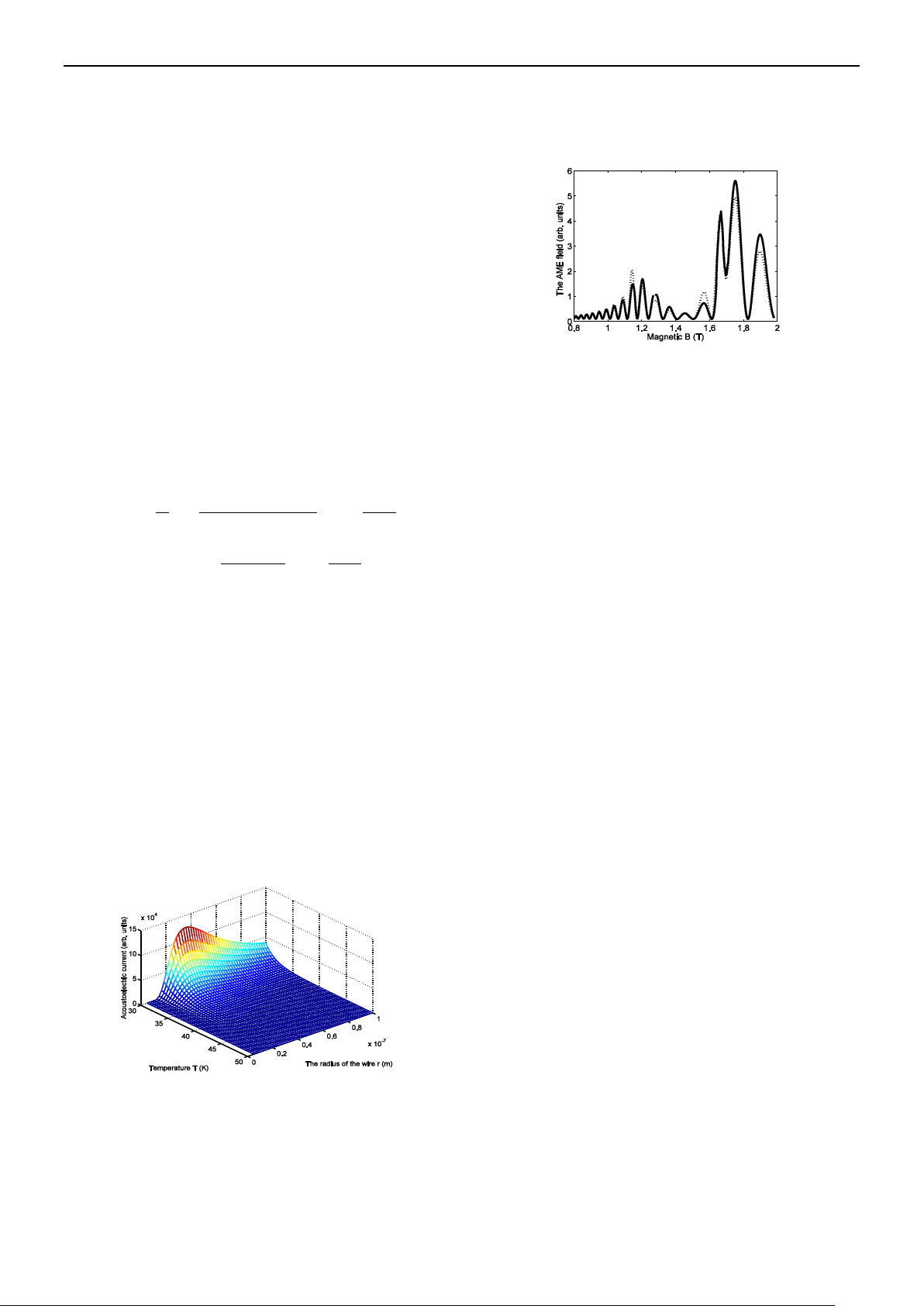
Hình 2. Sự phụ thuộc của trường AME
vào EMF, với R = 30 nm.
Hình 2 biểu diễn sự phụ thuộc của trường
AME vào EMF trong vùng từ trường mạnh
ứng với nhiệt độ T = 4,8K (đường đứt nét),
T = 5,0K (đường liền nét). Kết quả cho thấy có
sự khác biệt so với bán dẫn khối [1] nguyên
nhân là do phổ năng lượng của điện tử bị ảnh
hưởng bởi từ trường mạnh và sự tác động của
điện tử giam cầm trong CQWIP. Kết quả này
có phần giống với hố lượng tử [3] nhưng có giá
trị lớn hơn bởi vì trong [3] chỉ tính đến sự
tương tác giữa điện tử và sóng âm ngoài,
nhưng bài viết này được xem xét khi điện tử
tương tác với sóng âm ngoài và sự tán xạ của
sóng âm trong với điện tử trong mẫu bán dẫn.
4. KẾT LUẬN
Trong bài báo này, chúng tôi đã sử dụng
phương pháp phương trình động lượng tử để
nghiên cứu hiệu ứng AE và AME trong
CQWIP thu được biểu thức giải tích cho dòng
AE và trường AME trong CQWIP. Kết quả lý
thuyết của dòng AE và trường AME đã được
tính toán, vẽ đồ thị và biện luận với CQWIP
AlGaAs/GaAs. Các kết quả này được so sánh
với bán dẫn khối, siêu mạng và hố lượng tử.
Ngoài ra, kết quả còn cho thấy sự phụ thuộc
của dòng AE và trường AME vào hình học của
dây do sự giam hãm điện tử trong CQWIP.
5. Tµi liÖu tham kh¶o
[1] E. M. Epshtein, Y. V. Gulyaev, (1967),
Sov. Phys. Sol. State., 9 (N.2), 288.
[2] J. M. Shilton, D. R. Mace, V. I. Talyanskii,
(1996), J. Phys. Condens. Matter., 8, 337.

Tuyển tập Hội nghị Khoa học thường niên năm 2015. ISBN : 978-604-82-1710-5
94
[3] N. Q. Bau, N. V. Hieu, N. V.
Nhan, (2012), Superlattices
and Micro., 52, 921.

Tuyển tập Hội nghị Khoa học thường niên năm 2015. ISBN : 978-604-82-1710-5
95











![Bài tập Vật lý sóng: Tổng hợp bài tập 6 [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250805/oursky04/135x160/401768817575.jpg)














