zunia.vn

Tuyển sinh 2024 dành cho Gen-Z

zunia.vn

» Tài Liệu Phổ Thông

» Đề thi - Kiểm tra

TRƯỜNG THPT TAM GIANG ĐÁP ÁN TOÁN KHỐI 10 HỌC KỲ I NĂM HỌC 2010-2011. Câu Ý Nội

Chia sẻ: Nguyen Phuong Ha Linh Linh | Ngày: | Loại File: PDF | Số trang:3

Báo xấu

70
lượt xem 6
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

TRƯỜNG THPT TAM GIANG ĐÁP ÁN TOÁN KHỐI 10 HỌC KỲ I NĂM HỌC 2010-2011. Câu Ý Nội dung A  1; 2;3 , B  3; 4 1 A  B  3 , A  B  1;2;3; 4 I 2 Điểm 0,5 0,5 0,5 0,5 x  1  0 Nêu được :   x2 x 1 Giải ra :  Tập xác định : D  1; 2    2;   x  2 Tập xác định: D  ¡ Tọa độ đỉnh: I (1; 4) a  1  0 : (P)quay bề...

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: TRƯỜNG THPT TAM GIANG ĐÁP ÁN TOÁN KHỐI 10 HỌC KỲ I NĂM HỌC 2010-2011. Câu Ý Nội

TRƯỜNG THPT TAM GIANG ĐÁP ÁN TOÁN KHỐI 10 HỌC KỲ I NĂM HỌC 2010-2011. 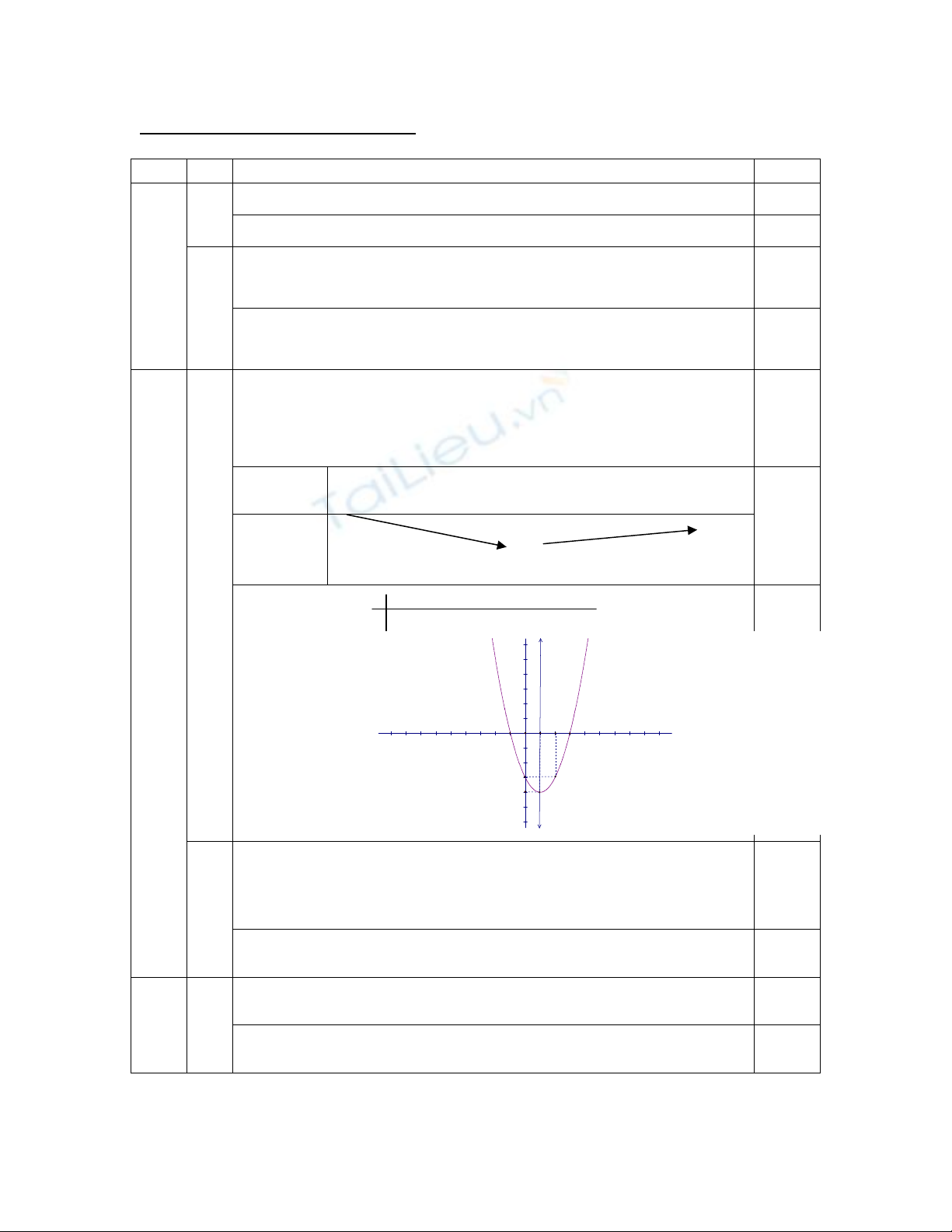C âu Ý Nội dung Điểm A  1; 2;3 , B  3; 4 0,5 1 A  B  3 , A  B  1;2;3; 4 0,5 0,5 x  1  0 I Nêu được :   x2 2 0,5 x 1 Tập xác định : D  1; 2    2;   Giải ra :  x  2 Tập xác định: D  ¡ Tọa độ đỉnh: I (1; 4) 0,5 a  1  0 : (P)quay bề lõm lên trên,nhận đường thẳng x  1 làm trục đối xứng  + x 1 0,5 + + y -4 Điểm đặc biệt: x -1 0 1 2 3 1 y 0 -3 -4 -3 0 Đồ thị: 6 4 2 3 2 -1 1 O 0,5 -5 5 -2 II -3 -4 I -6 Tọa độ giao điểm của (P) và (d) chính là nghiệm của hệ 0,25  y  x2  2x  3 phương trình :  2  y  x 3 Giải tìm được hai giao giao điểm :  0; 3 ,  3;0  0,25 uuu uuu r r uur 0,25 Gọi I là trung điểm của BC ,chỉ được : AB  AC  2 AI uur uuur uuu r III 1 0,25 Tìm được : AI  AC  2 AD
uuu 1 uuu 3 uuu r r r 0,5 Đưa đến : AD  AB  AC 4 4 uuu r uuu r 0,5 AB  ( 2; 2), AC  (2; 5) 2a r uuu uuu r r r uuu uuu r r 0,5 u  AB  AC  (0; 7), v  2 AB  3 AC  (10;11) 0,5  x  x  xB  xD ABCD hình bình hành   A C  y A  yC  y B  yD 2b 0,5  xD  x A  xC  xB  3 : D (3; 2)   y D  y A  yC  y B   2 m2  9 m  3 :Phương trình có nghiệm duy nhất x   m3 0,5 m3 1 m  3 :PT  0.x  0 Phương trình có vô số nghiệm x  ¡ 0,5 0,25 Đặt: t  x 2  0 đưa về : t 2  8t  15  0 0,25 t  3 Giải ra được :  2 t  5 0,5 t  3  x   3, t  5  x   5 IVa 1 1 Đặt : u  , v  với x  0, y  0 .Đưa về 0,25 x y  uv 3 u  2 3  HPT:  2u  v  5 v 1  1  u  2 x  0,25  2  v 1   y 1   0,25 A  sin 2   2cos 2  (1  cos 2 )  2cos 2  1  cos 2 4 2 0,25  1  10 A  1     3 9 0,5 m( x  3)  2 x  m 2  2  (m  2) x  m 2  3m  2 1 m  2 : Phương trình có một nghiệm duy nhất 0,25 m 2  3m  2 x  m 1 m2
m  2 : PT  0.x  0 Phương trình có vô số nghiệm x  ¡ 0,25 0,25 m0  mx 2  2 x  m  3  0 có hai nghiệm   / 2    m  3m  1  0 2 0,25 m  3  2 x12  x2  12  S 2  2 P  12      2.( 2 )  12  m m IVb 2 Đưa về phương trình : 10m 2  6m  4  0 .Giải ra 0,25  m 1 được:  m   2 5  0,25 2 Thử lại : loại m   Vậy : m  1 5 0,25 D  m(m  2)  3  m 2  2m  3 3 HPT có nghiệm duy nhất 0,25  m 1  D  0  m 2  2m  3  0    m  3 A  cos 4  sin 4   2sin 4   2sin 2   1 0,25 4 4 2 0,25  2  2 41 A  2.   2.   1  .  3  3 81 Chú ý : Nếu học sinh làm cách khác thì Giáo viên chấm căn cứ cách làm để cho các thành phần điểm tương ứng phù hợp.

CÓ THỂ BẠN MUỐN DOWNLOAD

THÔNG TIN

TRỢ GIÚP

HỖ TRỢ KHÁCH HÀNG

Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.