1
Chư ơ ng 5. Ư Ớ C LƯ Ợ NG VÀ KIỂ M ĐỊ NH GIẢTHUYẾT
5.1. Bài toán ư ớ c lư ợ ng
Trong phần này sẽ đề cậ p đế n việc suy luậ n các đặ c trư ng củ a tổng thểdự a trên các đặ c trư ng
của mẫ u. Các đặ c trư ng củ a tổng thểcó thểlà giá trịtrung bình, phư ơ ng sai hoặ c tỷlệ các đơ n vị
của tổng thểcó một tính chấ t nào đó.
Vấ n đề đặ t ra là ư ớ c lư ợ ng các đặ c trư ng củ a tổng thể (chư a biế t) từ các đặ c trư ng củ a mẫu dữ
liệu thu thậ p đư ợ c.
1. Các vấ n đề liên quan đế n bài toán ư ớ c lư ợ ng
Có hai loạ i ư ớ c lư ợ ng là ư ớ c lư ợ ng điể m và ư ớ c lư ợ ng khoảng.
Ư ớ c lư ợ ng điể mlà phư ơ ng pháp dùng một tham sốthống kê mẫuđơ n lẻ để ư ớ c lư ợ ng
vềgiá trịthật của tham sốtổng thể.
Các tham số đặ c trư ng
Mẫu
Tổng thể
Trung bình
Tỷlệ
Phư ơ ng sai
Do các tham số đặ c trư ng củ a tổng thể đư ợ c ư ớ c lư ợ ng thông qua một mẫ u đư ợ c chọn
nên khi thay đổ i từmẫu này sang mẫu khác sẽdẫ n đế n các tham số đặ c trư ng củ a tổng
thểcũng thay đổ i.
Vì vậ y, trong trư ờ ng hợp trung bình của tổng thểnếu dùng một giá trịtrung bình mẫu của
một mẫu cụthể để ư ớ c lư ợ ng điể m vềtrung bình tổng thểsẽkém tin cậ y hơ n so vớ i khi
vận dụng quy luật phân phối của trung bình mẫu vào quá trình ư ớ c lư ợ ng trung bình tổng
thể qua phư ơ ng pháp ư ớ c lư ợ ng khoảng.
Ư ớ c lư ợ ng khoảng là phư ơ ng pháp dự a vào dữliệu của mẫu, với mộ t độ tin cậy cho
trư ớ c, xác đị nh khoảng giá trị mà đặ c trư ng củ a tổng thểcó thể rơ i vào.
Một cách tổng quát, gọilà đặ c trư ng củ a tổng thểcầ n ư ớ c lư ợ ng. Giảsử, dựa vào mẫu
quan sát tìm đư ợ c hai biến ngẫu nhiên và sao cho (< < )= 1 − .
Gọi,lầ n lư ợ t là các giá trịcụthểcủa và . Khoảng ( , ) đư ợ c gọi là khoả ng ư ớ c
lư ợ ng vớ i độ tin cậy(1 − )∗100% của , hay nói một cách ngắn gọn là khoảng tin cậy
(1 − )∗100% của .
2. Ư ớ c lư ợ ng trung bình tổng thể
A. Ư ớ c lư ợ ng trung bình một tổng thể
a. Biế t phư ơ ng sai củ a tổng thể
Giảsửcó mẫuquan sát đư ợ c chọn ngẫu nhiên từtổng thểphân phối chuẩ n có phư ơ ng sai
đã biết.
Gọi là trung bình mẫu, khoảng tin cậy(1 − )∗100% của trung bình tổng thể đư ợ c xác
đị nh bởi
2
−/∗
√< < + /∗
√
Với có phân phối chuẩn.
Ví dụ:Một công ty muố n ư ớ c lư ợ ng sốtài liệ u (trang) đư ợ c chuyển bằng fax trong một ngày.
Kết quảthu thập từ15 ngày cho thấy trung bình một ngày có 267 trang tài liệ u đư ợ c chuyển
bằng fax. Theo kinh nghiệm từ các văn phòng tư ơ ng tự thì độ lệch chuẩn là 32 trang. Giảsửsố
trang tài liệu chuyển bằng fax trong một ngày có phân phối chuẩn vớ i độ tin cậ y 95%, ta ư ớ c
lư ợ ng
−/∗
√< < + /∗
√
Với= 267, = 32, = 15, /=.= 1.96 ta có 250.8055 < < 283.1945.
Như vậ y vớ i độ tin cậy 95%, số lư ợ ng tài liệu chuyển trung bình mộ t ngày đư ợ c ư ớ c lư ợ ng từ
251 đế n 284 trang.
Nhận xét:
Với mộ t độ tin cậ y và kích thư ớ c mẫukhông đổ i, nế u độ lệch chuẩn càng lớn thì
khoả ng ư ớ c lư ợ ng càng rộng, tứ c là độ chính xác củ a ư ớ c lư ợ ng càng thấp.
Với mộ t độ tin cậ y và độ lệch chuẩ n không đổ i, nế u kích thư ớ c mẫu càng lớn thì
khoả ng ư ớ c lư ợ ng càng hẹp, tứ c là độ chính xác củ a ư ớ c lư ợ ng càng cao.
Vớ i độ lệch chuẩ n và kích thư ớ c mẫukhông đổ i, nế u độ tin cậy càng cao thì khoảng
ư ớ c lư ợ ng càng rộng, tứ c là độ chính xác củ a ư ớ c lư ợ ng càng thấp.
b. Chư a biế t phư ơ ng sai củ a tổng thể
Trong thực tế , ta thư ờ ng không biế t phư ơ ng sai củ a tổng thể.
Trong trư ờ ng hợp này ta vẫn giả đị nh tổng thểcó phân phối chuẩn, khoảng tin cậy
(1 − )100% trung bình tổng thể đư ợ c xác đị nh như sau:
−, / ∗
√< < + , / ∗
√
Với có phân phối Student với bậc tựdo (− 1).
Ví dụ:Công ty điệ n thoạiởmột thành phốmuố n ư ớ c lư ợ ng thời giant rung bình của các cuộc
điệ n đàm đư ờ ng dài vào những ngày cuối tuần. Mẫu ngẫu nhiên 20 cuộc gọiđư ờ ng dài vào
những ngày cuối tuần cho thấy thờ i gian điệ n đàm trung bình là 14.8 phút, độ lệch chuẩn là 5.6
phút. Như vậ y vớ i độ tin cậy 95%, thời gian trung bình của cuộ c điệ n đàm đư ờ ng dài đư ợ c xác
đị nh như sau:
−, / ∗
√< < + , / ∗
√
3
Với= 14.8; = 5.6; = 20, , / =, . = 2.093 ta có
12.1792 < < 17.4208
Nghĩa là vớ i độ tin cậy 95%, thời gian trung bình của một cuộ c điệ n đàm đư ờ ng dài vào cuối
tuầ n đư ợ c ư ớ c lư ợ ng khoảng từ 12.1792 đế n 17.4208 phút.
Lư u ý: Trong trư ờ ng hợp mẫu lớn ( ≥ 30), ta có thểdùng phân phối chuẩn thay cho phân phối
Student, kểcả trong trư ờ ng hợp tổng thểcó phân phối chuẩn.
Ví dụ:Mộ t trư ờ ng đạ i học thực hiện nghiên cứu vềsốgiờtựhọc của sinh viên trong một tuần.
Chọn ngẫu nhiên 200 sinh viên cho thấy sốgiờtựhọc trong tuần tính trung bình là 18.36 giờ , độ
lệch chuẩn là 3.92 giờ . Như vậ y vớ i độ tin cậy 95%, sốgiờtựhọc trung bình của sinh viên ở
trư ờ ng này đư ợ c ư ớ c lư ợ ng là:
−/∗
√< < + /∗
√
Với= 18.36; = 3.92; = 200; /=.= 1.96 ta có
17.8168 < < 18.9032
Nghĩa là vớ i độ tin cậy 95%, sốgiờtựhọc trung bình trong tuần củ a sinh viên đư ợ c ư ớ c lư ợ ng từ
17.8168 đế n 18.9032 giờ.
B. Ư ớ c lư ợ ng sựkhác biệt giữa hai trung bình tổng thể
Trong nhiề u trư ờ ng hợp, ta có thể quan tâm đế n khác biệt giữa trung bình hai tổng thể, chẳng hạn
như khác biệ t vềdoanh sốtrung bình trong tuần từ hai phư ơ ng pháp trư ng bày hàng hóa, chào
hàng hóa khác nhau, hoặc sựkhác biệt giữ a năng suấ t cây trồng do sửdụng hai loại phân bón
khác nhau… Phư ơ ng pháp so sánh trung bình hai tổng thểphụthuộc vào cách thức lấy mẫu: mẫu
phối hợp từng cặp (mẫu phụthuộc) hoặc mẫ u độ c lập.
a. Mẫu phối hợp từng cặp
Ở phư ơ ng pháp này, các đơ n vị mẫ u đư ợ c chọn từng cặp, từhai tổng thể . Thông thư ờ ng mẫu
phối hợp từng cặ p thư ờ ng bao gồ m các trư ờ ng hợ p sau đây:
-So sánh trư ớ c và sau, chẳng hạn mẫu thứnhất là doanh số bán trư ớ c khi thực hiện
khuyến mãi, mẫu thứhai là doanh sốsau khi thực hiện khuyến mãi. Ở đây mẫ u phối hợp
từng cặp theo nghĩa là doanh số trư ớ c và sau khi khuyến mãi đư ợ c thu thập từcùng một
cửa hàng.
-So sánh các đơ n vị ở cùng mộ t đặ c điể m nào đó, chẳ ng hạn mẫu thứnhất là tiề n lư ơ ng
của nhân viên nam ởcông ty Y, mẫu thứhai là tiề n lư ơ ng củ a nhân viên nữ ở công ty Y,
hai nhân viên nam và nữ đư ợ c xem là giống nhau về năng lự c và kinh nghiệm. Ở đây,
mẫu phối hợp từng cặp theo nghĩa là cảhai nhân viên nam và nữ đư ợ c xem là có nang lực
và kinh nghiệ m như nhau.
4
- So sánh giữ a các đơ n vị phối hợp từng cặp theo không gian, chẳng hạn mẫu thứnhất là
doanh sốcủa loạ i nư ớ c giải khát nhãn hiệu A ởcửa hàng; ởmẫu thứhai là doanh số
bán hàng của loạ i nư ớ c giải khát nhãn hiệu B ởcử a hàng đó. Ở đây, mẫ u phối hợp từng
cặp theo nghĩa là cảhai doanh sốcủa hai nhãn hiệ u A và B đề u đư ợ c thu thập từcùng
một cửa hàng.
- So sánh giữ a các đơ n vị phối hợp từng cặp theo thời gian, chẳng hạn mẫu thứnhất là
doanh sốcủa nhà hàng X ởmột tuần lễ nào đó, mẫ u thứhai là doanh sốcủa nhà hàng Y
trong cùng một tuần lễ đó. Ở đây mẫ u phối hợp từng cặp theo nghĩa từ ng cặp doanh số
đư ợ c thu thập trong cùng một tuần lễ.
Giảsửcó các cặp quan sát ( , ) lấy ngẫu nhiên từhai tổng thểvà .
Gọi,lầ n lư ợ t là trung bình của tổng thể,;
là trung bình của khác biệt;
là độ lệch tiêu chuẩn của khác biệt.
Với khoảng tin cậy(1 − )100% của−đư ợ c xác đị nh như sau:
−, / ∗
√< − < +, / ∗
√
Với có phân phối Student với bậc tựdo (− 1).
Ví dụ:Công ty điệ n lực thực hiện các biện pháp khuyến khích tiết kiệmđiệ n. Lư ợ ng điệ n tiêu
thụghi nhậnở12 hộ gia đình trư ớ c và sau khi có các biện pháp khuyến khích tiết kiệm ddieemnj
như sau:
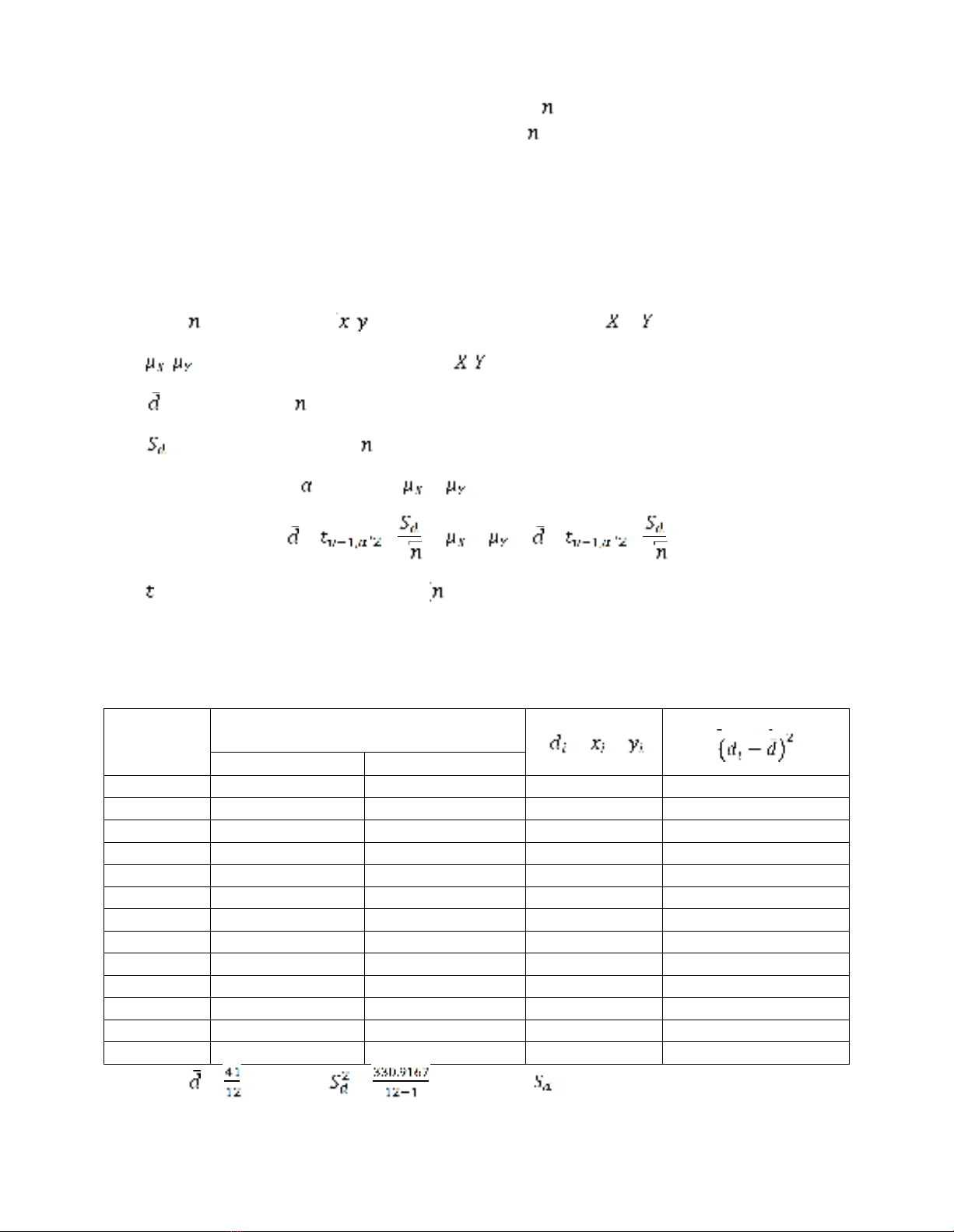
Hộ gia đình
Lư ợ ng điệ n tiêu thụ trư ớ c và sau khi
khuyến khích tiết kiệ m điệ n (KWh)
Độ lệch
= −
Bình phư ơ ng độ lệch
−
Trư ớ c
1
73
4
0.340278
2
50
-4
55.00694
3
83
1
5.840278
4
78
11
57.50694
5
56
-4
55.00694
6
74
1
5.840278
7
74
-1
19.50694
8
87
9
31.17361
9
69
5
2.506944
10
72
0
11.67361
11
77
7
12.84028
12
75
12
73.67361
Tổng
41
330.9167
Vậy ta có = = 3.4167;=.=30.08333↔ = 5.4848.
5
Giả sử rằ ng các khác biệ t giữ a lư ợ ng điệ n trư ớ c và sau khi khuyế n khích tiế t kiệ m điệ n có phân phố i
chuẩ n, khoả ng itn cậ y 95% củ a −là
−, / ∗
√< − < +, / ∗
√
Với= 12; = 3.4167; = 5.4848; , / =, . = 2.201 ta có
− 0.0682 < − < 6.9016
Như vậ y, khoảng tin cậy 95% của khác biệt giữ a lư ợ ng điệ n tiêu thụtrung bình trư ớ c và sau khi
khuyến khích tiết kiệ m đư ợ c ư ớ c lư ợ ng từ-0.0682 KWh đế n 6.9016 KWh. Khoả ng ư ớ c lư ợ ng
này bao gồm trịsố0, do vậy có thểtin rằ ng lư ợ ng điệ n tiêu thụtrung bình trư ớ c và sau khi thực
hiện các biện pháp khuyến khích tiết kiệm là bằng nhau.
b. Mẫ u độ c lập
Gọi,là các mẫ u đư ợ c chọn ngẫ u nhiên độ c lập từhai tổng thểphân phối chuẩn và ;
,là trung bình của hai tổng thểvà ;
,là phư ơ ng sai củ a hai tổng thểvà ;
,là trung bình của hai mẫu.
Khoảng tin cậy(1 − )100% của−đư ợ c xác đị nh như sau:
(−)−/∗+ < − < (−)+/∗ +
Với có phân phối chuẩn.
Ví dụ:Mộ t công ty đang xem xét kế hoạch tiết giảm chi phí sản xuất thông qua việc xây dựng
một dây chuyền sản xuất mới nhằm rút ngắn thời gian sản xuất sản phẩm. Ởdây chuyền sản
xuất mới 40 sản phẩ m đư ợ c sản xuất với thời gian trung bình 46.5 phút/sản phẩ m, độ lệch tiêu
chuẩn là 8 phút. Với dây chuyền sản xuất, 38 sản phẩ m đư ợ c sản xuất với thời gian trung bình
51.2 phút/sản phẩ m, độ lệch chuẩn 9.5 phút. Hãy ư ớ c lư ợ ng khoảng tin cậy 95% cho khác biệt về
thời gian sản xuất giữa dây chuyền sản xuất mới và cũ.
Ta có
= 46.5
= 8
= 40
/=.= 1.96
= 51.2
= 9.5
= 38
Ta có khoảng tin cậy 95% sựkhác biệt vềthời gian sản xuất trung bình giữa dây chuyền sản xuất
mới và cũ là