D ng : XÁC ĐNH GIÁ TR C C ĐI C A ĐI N ÁP HI U D NG KHI THAY ĐIạ Ị Ị Ự Ạ Ủ Ệ Ệ Ụ Ổ
THÔNG S C A M CHỐ Ủ Ạ
1.Các công th c c a các đi n áp hi u d ng c c đi khi thông s c a m ch thay đi:ứ ủ ệ ệ ụ ự ạ ố ủ ạ ổ
a. Đi n áp hi u d ng Uệ ệ ụ R:
+ R thay đi : UổR(max) = U Khi R
+ L,hay C, hay
ω
thay đi : UổR(max) = U Khi
1
LC
ω
=
( C ng h ngộ ưở )
b. Đi n áp hi u d ng : Uệ ệ ụ L
+ R thay đi : UổL(max) =
L
L C
UZ
Z Z−
khi R = 0
+ L thay đi : UổL(max) = IZL =
2 2
C
U R Z
R
+
khi ZL =
2 2
C
C
R Z
Z
+
+ C thay đi : UổL(max) = IZL =
L
UZ
R
khi C =
2
1
L
ω
( C ng h ngộ ưở )
+
ω
thay đi : UổL(max) = IZL khi
ω
=
c. Đi n áp hi u d ng : Uệ ệ ụ C
+ R thay đi : UổC(max) =
C
L C
UZ
Z Z−
khi R = 0
+ C thay đi : UổC(max) = IZC =
2 2
L
U R Z
R
+
khi ZC =
2 2
L
L
R Z
Z
+
+ L thay đi : UổC(max) = IZC =
C
UZ
R
khi L =
2
1
C
ω
( C ng h ngộ ưở )
+
ω
thay đi : UổC(max) = IZC khi
ω
=
2
2
1
2
R
LC L
−
2. Công th c th ng g p c n nh khi L,C, f thay đi (ứ ườ ặ ầ ớ ổ không C ng h ngộ ưở ) :
Tìm L đ Uể Lmax:( M ch đi n hình v bên ph i khi L thay đi)ạ ệ ẽ ả ổ
2 2
C
Lmax
R + Z
U = U R
V i ớ
2 2
C
L
C
R + Z
Z = Z
=>
2 2
C
C
R + Z
L = Zω
Tìm C đ Uể Cmax:( M ch đi n hình v bên ph i khi C thay đi)ạ ệ ẽ ả ổ
L
2 2
Cmax
R + Z
U = U R
V i ớ
2 2
L
C
L
R + Z
Z = Z
=>
L
2 2
L
Zω
C = R + Z
Xác đnh giá tr c c đi Uị ị ự ạ Lmax, và UCmax khi t n s f thay đi:ầ ố ổ
max max 2 2
2
4
L C
LU
U U
R LC R C
= = −
Khi:
2
1 2
L
C
C
ω
OL
=
2 - R
;
2
1
2
L
C
L
ω
OC
2 - R
=
S u t m: ư ầ Đòan văn L ng - Email: ượ doanvluong@yahoo.com ; doanvluong@gmail.com Trang 1
C
AB
RL
V
C
AB
RL
V
(v i đi u ki n ớ ề ệ
2
2LR
C>
)
3. Bài t p v xác đnh giá tr c c đi Uậ ề ị ị ự ạ max khi thay đi L, ho c C, ho c f.ổ ặ ặ
a.Các ví d :ụ
+Ví d 1ụ : Cho m ch đi n nh hình v . Đi n áp gi a hai đu AB có bi u th c ạ ệ ư ẽ ệ ữ ầ ể ứ
200cos100u t
π
=
(V). Cu n ộ
dây thu n c m có L thay đi đc, đi n tr R = 100ầ ả ổ ượ ệ ở ,
t đi n có đi n dung ụ ệ ệ
4
10
C
π
−
=
(F). Xác đnh L sao cho đi n áp ị ệ
hi u d ng gi a hai đi m M và B đt giá tr c c đi, tính h s công su t c a m ch đi n khi đó.ệ ụ ữ ể ạ ị ự ạ ệ ố ấ ủ ạ ệ
Bài gi iả: Dung kháng:
4
1 1 100
10
100 .
C
ZC
ωππ
−
= = = Ω
Cách 1: Ph ng pháp đo hàmươ ạ
Ta có:
( )
( )
2
22 2
2
1 1
2 1
AB L AB AB
MB L
L C C C
L L
U Z U U
U IZ y
R Z Z R Z Z
Z Z
= = =
+ − + − +
max
min
L
U
Uy
=
v i ớ
( ) ( )
2 2 2 2 2
2
1 1
2 1 2 . 1
C C C C
L L
y R Z Z R Z x Z x
Z Z
= + − + = + − +
(v i ớ
1
L
xZ
=
)
Kh o sát hàm s y:ả ố Ta có:
( )
2 2
' 2 2
C C
y R Z x Z
= + −
.
( )
2 2
2 2
' 0 2 2 0
C
C C
C
Z
y R Z x Z x R Z
= + − = =� � +
B ng bi n thiên: ả ế
ymin khi
2 2
C
C
Z
xR Z
=+
hay
2 2
1
C
L C
Z
Z R Z
=+
2 2 2 2
100 100 200
100
C
L
C
R Z
ZZ
+ +
= = = Ω�
200 2
100
L
Z
L
ω π π
= = =�
H ; H s ệ ố
( )
( )
2 2
2
2
100 2
cos 2
100 200 100
L C
R
R Z Z
ϕ
= = =
+ −
+ −
Cách 2: Ph ng pháp dùng tam th c b c haiươ ứ ậ
Ta có:
( )
( )
2
22 2
2
1 1
2 1
AB L AB AB
MB L
L C C C
L L
U Z U U
U IZ y
R Z Z R Z Z
Z Z
= = =
+ − + − +
Đt ặ
( )
2 2 2
2
1 1
2 1 1
C C
L L
y R Z Z ax bx
Z Z
= + − + = + +
V iớ
1
L
xZ
=
;
2 2
C
a R Z= +
;
2
C
b Z= −
UMBmax khi ymin: Vì
2 2
C
a R Z= +
> 0 nên tam th c b c hai đt c c ti u khi ứ ậ ạ ự ể
2
b
xa
= −
hay
( )
2 2
2 2
1 2
2
C C
L C
C
Z Z
Z R Z
R Z
−
= − = +
+
2 2 2 2
100 100 200
100
C
L
C
R Z
ZZ
+ +
= = = Ω�
;
200 2
100
L
Z
L
ω π π
= = =�
H
S u t m: ư ầ Đòan văn L ng - Email: ượ doanvluong@yahoo.com ; doanvluong@gmail.com Trang 2
C
AB
RL
V
M
H s công su t:ệ ố ấ
( )
( )
2 2
2
2
100 2
cos 2
100 200 100
L C
R
R Z Z
ϕ
= = =
+ −
+ −
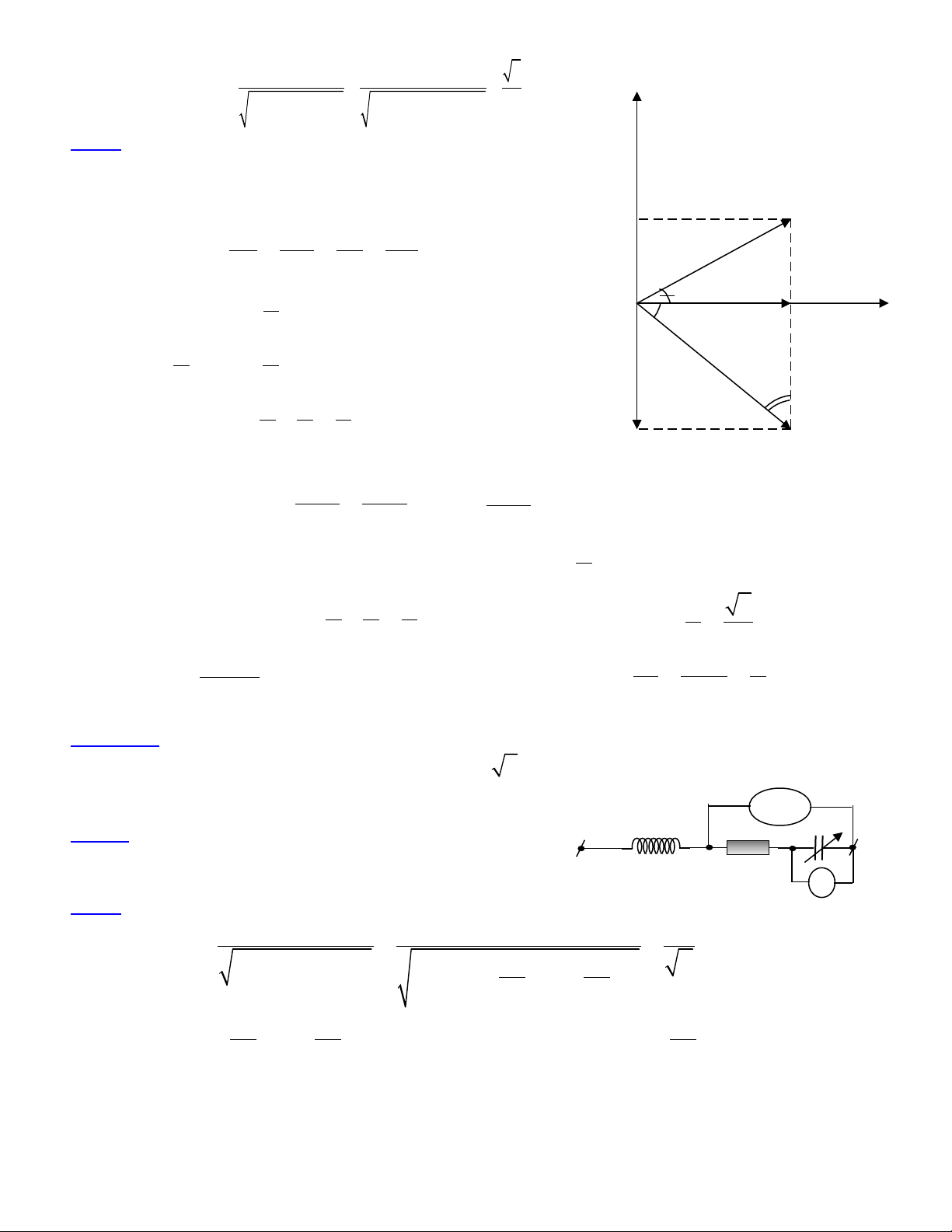
Cách 3: Ph ng pháp dùng gi n đ Fre-nenươ ả ồ .
R C L
U U U U= + +
ur uur uur uur
Đt ặ
1R C
U U U= +
uur uur uur
Ta có:
1
100
tan 1
100
C C C
R
U IZ Z
U IR R
ϕ
= = = = =
1
4
π
ϕ
=�
rad
Vì
1
2
π
α ϕ
+ =
1
2
π
α ϕ
= −�
2 4 4
π π π
α
=−=�
rad
Xét tam giác OPQ và đt ặ
1
β ϕ ϕ
= +
.
Theo đnh lý hàm s sin, ta có: ị ố
sin sin
L
U U
α β
=
sin
sin
L
U
U
β
α
=�
Vì U và sin không đi nên UổLmax khi sin c c đi hay sinự ạ = 1
2
π
β
=�
Vì
1
β ϕ ϕ
= +
1
2 4 4
π π π
ϕ β ϕ
= − = − =�
rad. H s công su t: ệ ố ấ
2
cos cos 4 2
π
ϕ
= =
M t khác ặ
tan 1
L C
Z Z
R
ϕ
−
= =
100 100 200
L C
Z Z R
= + = + = Ω�
200 2
100
L
Z
L
ω π π
= = =�
+Ví d 2ụ : M ch đi n nh hình v . Cu n dây thu n c m có đ t c m L = 0,318H, R = 100ạ ệ ư ẽ ộ ầ ả ộ ự ả , t C là t xoay.ụ ụ
Đi n áp đt vào hai đu đo n m ch có bi u th c ệ ặ ầ ạ ạ ể ứ
200 2 cos100u t
π
=
(V).
a. Tìm C đ đi n áp gi a hai đu b n t đt giá tr c c đi, tính giá tr c c đi đó.ể ệ ữ ầ ả ụ ạ ị ự ạ ị ự ạ
b. Tìm C đ đi n áp hai đu MB đt c c đi, tính giá tr c c đi đó.ể ệ ầ ạ ự ạ ị ự ạ
Bài gi iả:
a. Tính C đ UểCmax.
C m kháng : ả
100 .0,318 100
L
Z L
ω π
= = = Ω
Cách 1: Ph ng pháp đo hàmươ ạ :
Ta có:
( )
( )
2
22 2
2
1 1
2 1
C
C C
L C L L
C C
UZ U U
U IZ y
R Z Z R Z Z
Z Z
= = = =
+ − + − +
Đt ặ
( ) ( )
2 2 2 2 2
2
1 1
2 1 2 . 1
L L L L
C C
y R Z Z R Z x x Z
Z Z
= + − + = + − +
(v i ớ
1
C
xZ
=
)
UCmax khi ymin.
Kh o sát hàm s : ả ố
( )
2 2 2
2 . 1
L L
y R Z x x Z= + − +
( )
2 2
' 2 2
L L
y R Z x Z= + −�
S u t m: ư ầ Đòan văn L ng - Email: ượ doanvluong@yahoo.com ; doanvluong@gmail.com Trang 3
I
r
C
U
uur
U
ur
L
U
uur
R
U
uur
1
U
uur
ϕ
α
1
ϕ
O
P
Q
RCL
M
NB
A
V
V’
' 0y=
( )
2 2
2 2 0
L L
R Z x Z+ − =�
2 2
L
L
Z
xR Z
=�+
B ng bi n thiên: ả ế
ymin khi
2 2
L
L
Z
xR Z
=+
hay
2 2
1
L
C L
Z
Z R Z
=+
2 2 2 2
100 100 200
100
L
C
L
R Z
ZZ
+ +
= = = Ω�
5
1 1 5.10
100 .200
C
CZ
ω π π
−
= = =�
F
2 2 2 2
max
200 100 100 200 2
100
L
C
U R Z
UR
++
= = =
(V)
Cách 2: Ph ng pháp dùng tam th c b c haiươ ứ ậ .
Ta có:
( )
( )
2
22 2
2
1 1
2 1
C
C C
L C L L
C C
UZ U U
U IZ y
R Z Z R Z Z
Z Z
= = = =
+ − + − +
Đt ặ
( )
2 2 2
2
1 1
2 1 1
L L
C C
y R Z Z ax bx
Z Z
= + − + = + +
(v i ớ
1
C
xZ
=
;
2 2
L
a R Z= +
;
2
L
b Z= −
)
UCmax khi ymin. Vì hàm s y có h s góc a > 0, nên y đt c c ti u khi: ố ệ ố ạ ự ể
2
b
xa
= −
hay
2 2
1
L
C L
Z
Z R Z
=+
2 2 2 2
100 100 200
100
L
C
L
R Z
ZZ
+ +
= = = Ω�
4
1 1 10
100 .200 2
C
CZ
ω π π
−
= = =�
(F).
2 2 2 2
max
200 100 100 200 2
100
L
C
U R Z
UR
++
= = =
V
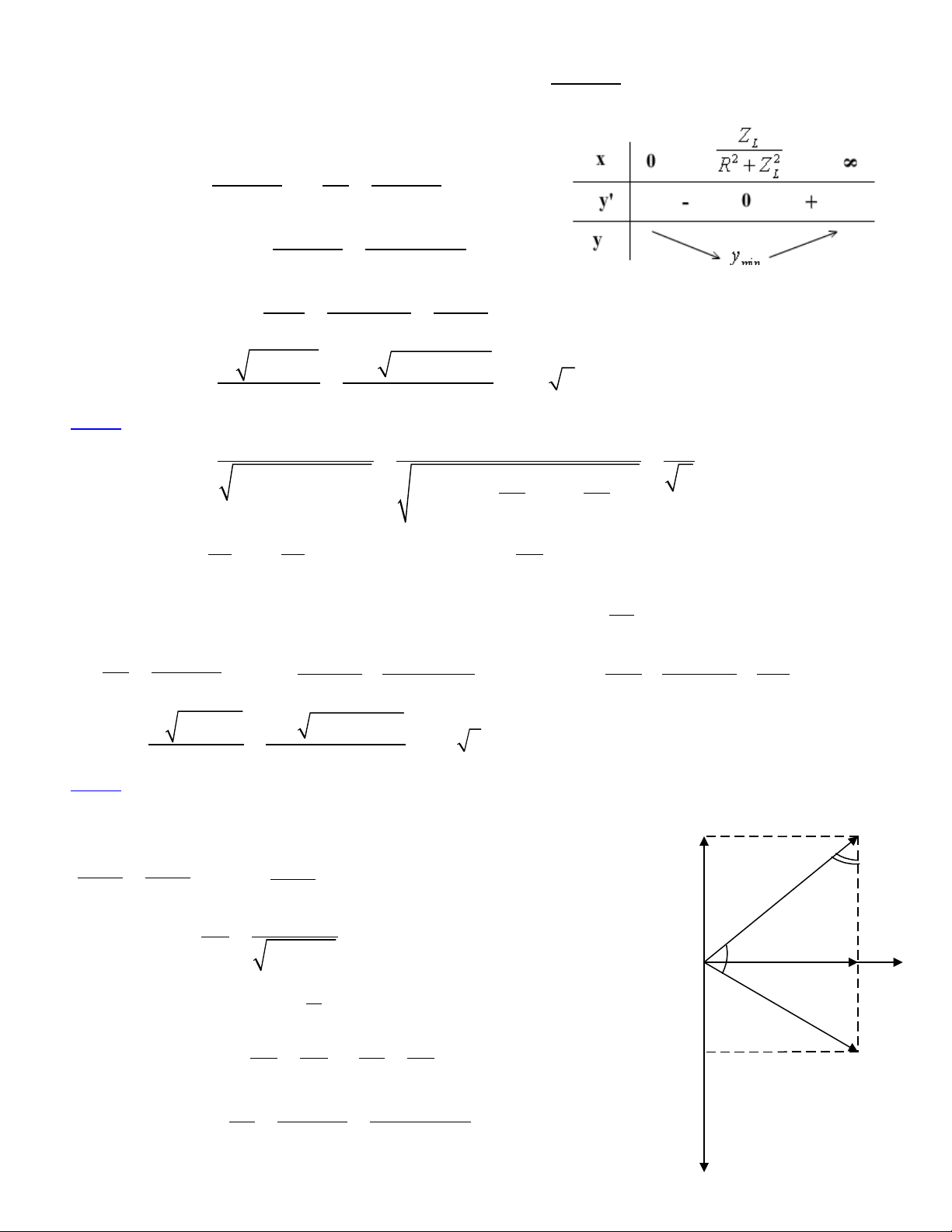
Cách 3: Ph ng pháp dùng gi n đ Fre-nenươ ả ồ .
Ta có:
L R C
U U U U= + +
ur uur uur uur
Áp d ng đnh lý hàm s sin, ta có:ụ ị ố
sin sin
C
U U
α β
=
sin
sin
C
U
U
β
α
=�
Vì U và
2 2
1
sin
R
L
U R
UR Z
α
= = +
không đi nên UổCmax khi sin c c đi hayự ạ
sin = 1. Khi
sin 1 2
π
β β
= =�
1 1
1 1
cos
L L
C C
U U Z Z
U U Z Z
α
= = =� �
2 2 2 2 2
1
100 100 200
100
L
C
L L
Z R Z
ZZ Z
+ +
= = = = Ω�
S u t m: ư ầ Đòan văn L ng - Email: ượ doanvluong@yahoo.com ; doanvluong@gmail.com Trang 4
I
r
C
U
uur
1
U
uur
L
U
uur
R
U
uur
U
ur
β
α
O
P
Q
5
1 1 5.10
100 .200
C
CZ
ω π π
−
= = =�
F
2 2 2 2
max
200 100 100 200 2
100
L
C
U R Z
UR
++
= = =
(V)
b. Tìm C đ UểMbmax. UMBmax = ?
L p bi u th c:ậ ể ứ
2 2 2 2
2 2
2 2 1
MB
MB MB
L L C C L L C
C
UZ U U
U IZ y
R Z Z Z Z Z Z Z
R Z
= = = =
+ − + − +
+
Đt ặ
2 2
2 2 2 2
2 2
1 1
L L C L L
C
Z Z Z Z Z x
yR Z R x
− −
= + = +
+ +
(v i x = ZớC)
UMBmax khi ymin:
Kh o sát hàm s y: ả ố
( )
( )
2 2
2
2 2
2 .
'
L L
Z x x Z R
y
R x
− −
=+
Ta có:
2 2
' 0 0
L
y x xZ R
= − − =�
(*)
Gi i ph ng trình (*) ả ươ
2 2
4
2
L L
C
Z Z R
x Z + +
= =
(x l y giá tr d ng).ấ ị ươ
( )
2 2 2
100 100 4.100 50 1 5 162
2
C
Z
+ +
= = + = Ω�
L p b ng bi n thiên: ậ ả ế
đi n dung ệ
4
1 1 0,197.10
100 .162
C
CZ
ω π
−
= = =
F;Thay
2 2
4
2
L L
C
Z Z R
x Z
+ +
= =
vào bi u th c yể ứ
()
2 2
min 2
2 2 2 2 2 2
4 4
4 2 2 4 4
L L L L L
R R
y
R Z Z Z R Z R Z
= =�+ + + + +
()()
2 2 2 2
max
min
4 200 100 100 4.100
324
2 2.100
L L
MB
U Z Z R
U
UR
y
+ + + +
= = = =
(V)
+Ví d 3ụ : Đt đi n áp xoay chi u u=Uặ ệ ề 0cost (U0 không đi và ổ thay đi đc) vào hai đu đo n m ch g m đi nổ ượ ầ ạ ạ ồ ệ
tr thu n R,cu n c m thu n có đ t c m L và t đi n có đi n dung C m c n i ti p,v i ở ầ ộ ả ầ ộ ự ả ụ ệ ệ ắ ố ế ớ CR2< 2L. Khi = 1 ho c ặ
= 2 thì đi n áp hi u d ng gi a hai đu cu n c m có cùng m t giá tr .Khi ệ ệ ụ ữ ầ ộ ả ộ ị = 0 thì đi n áp hi u d ng gi a hai ệ ệ ụ ữ
đu cu n c m có giá tr c c đi.H th c liên h gi a ầ ộ ả ị ự ạ ệ ứ ệ ữ 1,2 và 0 là :
A.
)(
2
12
2
2
1
2
0
B.
)(
2
1
210
C.
2
0
1
=
2
1
(
2
1
1
+
2
2
1
) D. 0 =
21
Gi iả: UL =
22 )( CL
L
ZZR
UZ
. Do UL1 = UL2 =>
2
1
1
2
2
1
)
1
(C
LR
=
2
2
2
2
2
2
)
1
(C
LR
S u t m: ư ầ Đòan văn L ng - Email: ượ doanvluong@yahoo.com ; doanvluong@gmail.com Trang 5