Ảnh hưởng của hệ số đất thấm lên các thông số dòng thấm ở đất thân và nền đập

www.vncold.vn

NH HNG CA HSTHMTTHÂN VÀ NNP

LÊN CÁC THÔNG SDÒNG THM

THE BODY AND BASE DAM PERMEABILITY EFFECT

ON INFILTRATION FLOW DATA

TS. Tô Vn Thanh

TÓM TT

Trong thc t!xây dng công trình th'y, r)tkhó ,- xác ,/nh chính xác

giá tr/h2s4th)m c'a m6t l8p,)t. V8icác ph:;ng pháp và ph:;ng

ti2n k>thu@t hi2nnay cAng chBgiúp các nhà khDosát thi!t l@p,:Ec

khoDng giá tr/bi!n,6ng c'a chúng mà thôi. Chính v@y, ,òi hHi các

nhà thi!t k!phDi dbáo ,:Ec phIm vi dao ,6ng c'a các thông s4dòng

th)m, nh:l:u l:Eng và gradient th)mtrong khoDng bi!n,Ki c'a h2s4

th)m (,Mc bi2t,4i v8i nhNng công trình có ,iOu ki2n,/a ch)t phPc

tIp), ,- k/pthRi,:ara các bi2npháp ,Dm bDo s Kn,/nh th)mcho

công trình. Bài vi!t gi8i thi2u ph:;ng pháp và k!t quDnghiên cPu s

Dnh h:Ung h2s4th)m c'a các l8p,)t nOn,@p,)t lên các thông s4

c'adòng th)mthông qua vi2c giDi các dIng bài toán th)m.

ABSTRACT

In practical construction of hydrology structures, it’s difficult to specify

the permeability of one soil layer exactly. Contemporary methods an

engineering facilities could only help the investigators set up

permeability fluctuation range. Therefore, designers have to anticipate

the fluctuation range of infiltration flow data. Such as the capacity and

infiltration gradient transformation range of permeability (especially at

complicated geological condition structures) to bring out timely

solutions ensuring stable infiltration for the project. This paper

presents method and research results about the effect of dam ground

base layers’ permeability on infiltration flow data by solving the

infiltration problem.

I. $T VN

Mttrong nhng vn quan trng nht cn phi gii quyt khi thit k

công trình thy là d!báo ch thm ca h%th&ng “công trình - nn”. S!ph,c

t-p ca nhng bài toán này ./c th0hi%n1ch2: cn phi tính nhàng lo-tcác

yu t&tác ng, nh.:6ahình; các iu ki%n6a chtcông trình; các 8cthù kt

www.vncold.vn

cu cacông trình c:ng nh.các bi%n pháp và kt cu ch&ng thm1thân và nn

công trình; khn<ng dao ng m!c n.=c1th./ng h-l.uv.v… ? chính xác

trong d!báo thm qua công trình còn phBthuc rt nhiu vào  chính xác trong

xác 6nh các tính cht thm ca các lo-it1thân và nn caCpt. M8c dù,

ãcó nhiu thành t!u vphát tri0ncác ph.Fng pháp và ph.Fng ti%n kGthuCt

nhHm xác 6nh các tính cht cFlý cat, vi%c thit lCpcác mô hình tin cCy v

6a cht thy v<n ca h%th&ng “Cp-nn” vJnlà vn ph,c t-pvà ch.a./c

gii quyt tri%t0. Tr6s&h%s&thmtrong mt l=pt có th0khác nhau hàng

chBc, thCm chí hàng tr<m ln. Trong nncó kt cu6a tng nhiu l=p ph,c t-p,

giá tr6tính toán các thông s&ca dòng thm phBthucvào s!t.Fng tác cacác

h%s&thm giacác l=pt nn. Mgiai o-n thit k Cpt, iuquan trng cn

phi d!báo ./c khong dao ng ca l.u l./ng, gradient thmvà v6trí .Ong

bão hòa, trên cFs1 ó.a ra các bi%n pháp ch&ng thm cho công trình. Chính vì

vCy, vi%cnghiên c,unh h.1ng h%s&thm cacác l=pt nntrong iu ki%n

6a cht ph,c t-p lên các thông s&dòng thm là ht s,c cn thit.

II. N%IDUNG, PH(NG PHÁP VÀ K*T QUNGHIÊN C,U

?&i t./ng nghiên c,u./c chn là Cptá thuc cBmcông trình thy

Jumaguzin trên sông Belaia (Liên bang Nga). Thân Cp./cxây d!ng bHng á

Y v=i vCt ch&ng thmlà lõi gia th[ng ,ng bHng á sét. ?Cpcó chiu dài 595m

v=i chiucao l=n nht là 70m. Thông th.Ong, &i v=i d-ng Cpnh.trên, vi%c

tính toán thm chacn thông qua gii bài toán ph[ng là -tyêu cu. Tuy nhiên,

b,ctranh 6a cht trong nn công trình này rt ph,c t-p, 8c tr.ng b1i tính không

bng nht vcác tính cht thm ca các l=pt d.=i thân Cp. Trên hình 1, th0

hi%n m8t cdt dc caCp, v=i nncông trình bao gbm sáu l=ptcó các giá tr6h%

s&thmkhác nhau (0 Fn gin hóa tính toán, mt s&l=ptcó h%s&thm xp

xanh.nhau ã./cquy vmt l=p). D.=i thân Cpcó b&trí các kt cu ch&ng

thmkhác nhau phBthuc vào iu ki%n6a cht1tfng nFi: t-i lòng sông, nFi

các l=pt nn phía trên có tính thm cao, d.=i lõi giaCpn sâu 30m, b&

trí n<mdãy màng ch&ng thm phun xi m<ng, tf  sâu 30 n120m – hai dãy

màng ch&ng thmphun xi m<ng. Mnn s.On d&c bOphi, trong ph-m vi các l=p

trmtích aluvi, n sâu 45m vCt ch&ng thm là “tng trong t” bHng bê

tông, tf  sâu 45 n120m - hai dãy màng phun xi m<ng. ?0 ng<n ngfa thm

vòng qua các vai Cp, t-o 2 dãy màng phun xi m<ng vào sâu 150m m2ibên vai

Cp. Do tính ph,c t-p ca6a cht nn công trình và s!thay Yi kt cu ch&ng

thm dctheo thân Cp, nên cn thit phicó s!so sánh lOi gii gia bài toán

thm ph[ng và thm không gian.

?0 gii bài toán 8t ra nói trên, skdBng phn mmFILTR, ./cxây d!ng

t-i Bmôn Công trình Thy, tr.Ong TYng h/pXây d!ng Qu&cgia Mát-xcF-va

(MGSU), d!a trên ph.Fng pháp phn tkhu h-n kt h/p bin phân cBc b[1].

Mô hình FILTR ./cxây d!ng trên c1s1tìm nghi%m ca ph.Fng trình vi phân

www.vncold.vn

cFbn calý thuytthm (ph.Fng trình Poison) cho bài toán thm không gian

không Yn6nh:

xyz

d dH d dH d dH dH

K + K + K - = 0

dx dx dy dy dz dz dt





 



 

 (1)

Trong ó, H=f(x,y,z,t): Hàm ct n.=c thmbinYitheo thOigian;

kx, ky, kz: H%s&thm ca vCt li%u theo các ph.Fng ta X, Y, Z

: H%s&nhn.=c.

Tìm nghi%m caph.Fng trình (1) là mtiu ht s,ckhó kh<n. Trong bài

này, vi%cxác 6nh giá tr6ct n.=cthm./ctinhành trong quá trình c!cti0u

hóa hàm s&nào ó, hàm này ./cchnsao cho có th0xây d!ng ./cthuCttoán

0 giitrên cFs1ph.Fng pháp phn tkhu h-nvà ph.Fng pháp binphân cBc b.

Nu nh.githit rHng hàm cn tìm có d-ng:



2 2

2xyz

HHHH

K K K H dxdydz

xyzt













 

++ +







 



 











(2)

Theo 6nh lý Eiler, hàm s&}s• -tgiá tr6c!c ti0u nuhàm s&trong du

tích phân ca nó: f















,...

,H th€a mãn ph.Fng trình Eiler:





























f+y























































z•





= 0 (3)

Nghi%m ca ph.Fng trình (3) c:ng s•là nghi%m ca ph.Fng trình (1), nu

nh.thay thvào nó bi0u th,ctrong dutích phân ca ph.Fng trình (2) s•thu

./c ph.Fng trình Poison (1).

Vì vCy, vi%c gii caph.Fng trình (1) c:ng bng nghƒa v=i tìm giá tr6c!c

ti0u ca hàm (2).

Ph.Fng pháp gii các bài toán thm và thuCt toán c!c ti0u hóa ph.Fng

trình (2) ./c trình bày chi tit t-i [1,3].

www.vncold.vn

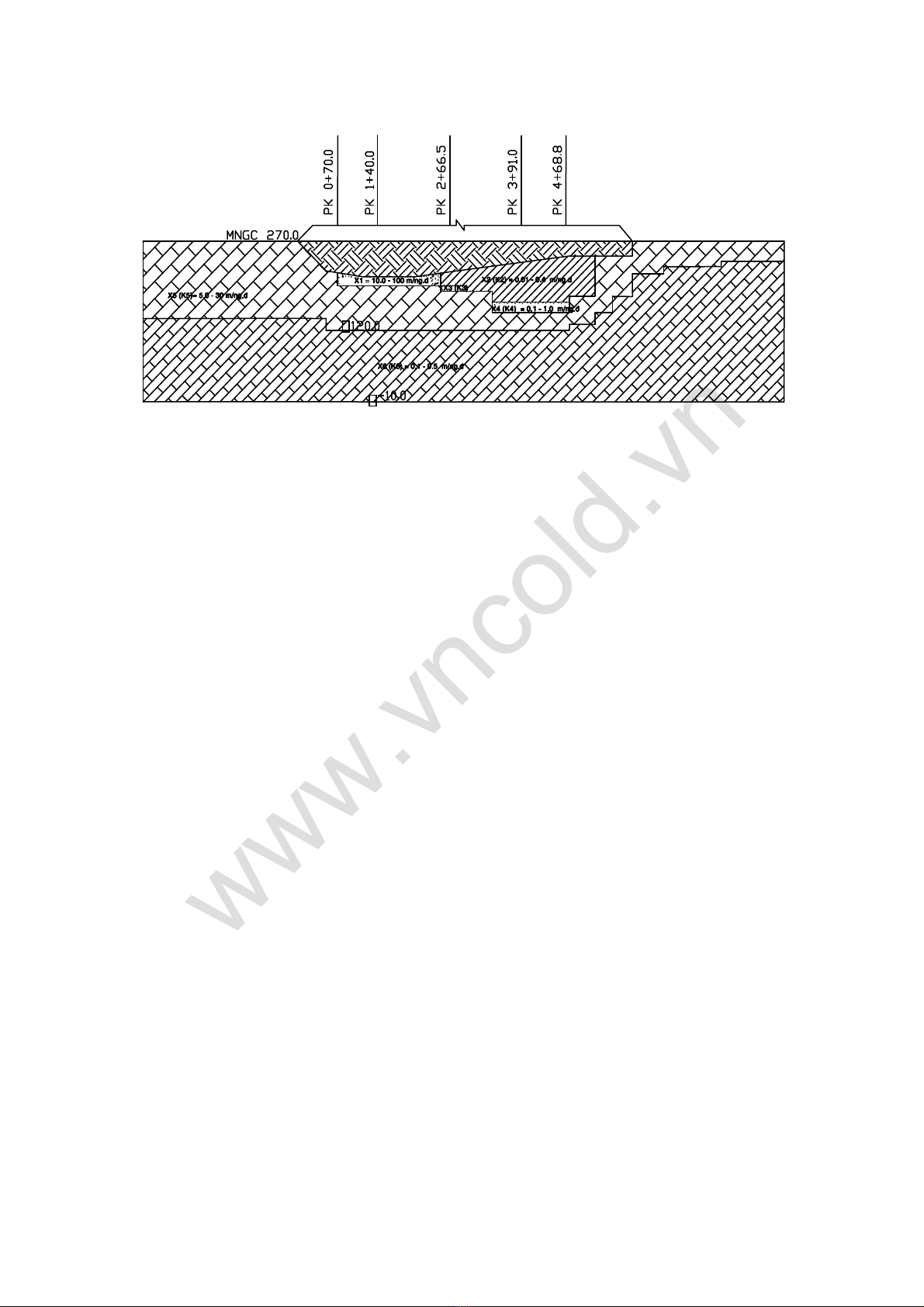
Hình 1: pt Jumaguzin-m t c"t d#c thân p

Mgiai o-nu, bài toán thm./c gii d.=i d-ng thm ph[ng cho 5 m8t

cdtPK 0+70, PK 1+40, PK 2+66,5, PK3+91, và PK 4+68,8. V6trí các m8t cdt

này ./c th0hi%n t-ihình 1. Vùng tính toán thm ca m2i m8t cdt bao gbmlõi

Cp bHng á sét và nn thm v=i các l=pt không bng cht (kích th.=c vùng

tính toán cho các m8t cdt./c th0hi%n t-i hình 2 và 3). Các l<ng trBbên bHng s€i

và á cui không .avào vùng tính toán do chúng có tính thm rt l=n (h%s&

thm ca vCt li%unày l=n gp khong 9.000 ln so v=i lõi Cp).

?0 nghiên c,u s! nh h.1ng ca h%s&thmt nn (h%s&thm ca lõi

Cp./ccoi là hHng s&) lên các thông s&ca dòng thm,ng dBng lý thuytquy

ho-ch th!c nghi%m [4].

Mm2i m8t cdt, h%s&thm cacác l=pt nnkhác nhau ./cxem là các

yu t&(các bin s&)nh h.1ng n l.u l./ng qua m2i m8t cdtang xét và

gradient thm phân b&theo trBc ca màng hay t.Ong ch&ng thm. S&l./ng các

l=pt nn v=icác tính cht thmkhác nhau (các bin s&)thay Yi tf2 (PK

0+70, PK 4+68,8) n 4 (PK3+91). T-i các m8t cdtPK 1+40 và PK 2+66,5, s&

l./ng bin bHng 3.

?0 ti%n cho vi%ctính toán, h%s&thm vCtlý cat nn./c ký hi%u là

X. M2i bin s&(h%s&thm ca l=pt nn) ./c ly 2 giá tr6:1m,c thp nht

và m,ccao nht (trong ph-m vi tip nhCn) và ./c ký hi%u t.Fng ,ng là -1 và +1

(Xi=±1). ?&i v=icác m8t cdtcó s&bin‡3, 0 có th0mô ph€ng ht khn<ng

t.Fng tác giacác giá tr6ca bin s&,áp dBng ph.Fng pháp quy ho-ch th!c

nghi%my [4]. Khi óhàm mBctiêu cn xét (l.u l./ng ho8c gradient thm)

có d-ng nh.sau.



Lõi /0pK=0.01 m/ng./

www.vncold.vn

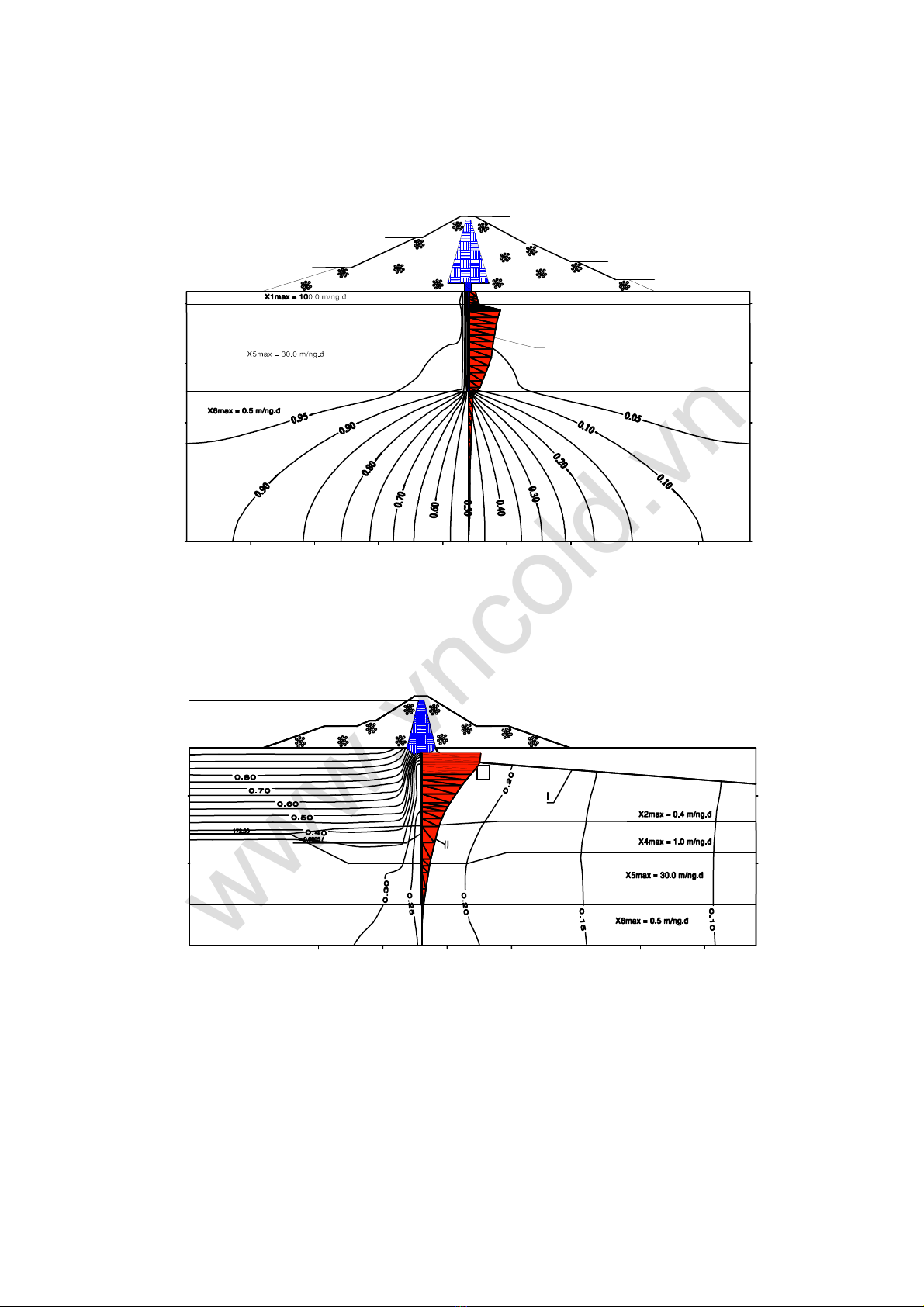
- V&i m t c"t PK 1+40:

Yi= bo+ b1X1+ b5X5+ b6X6+ b15 X1X5+ b16 X1X6+ b56 X5X6+ b156 X1X5X6(4)

Hình 2: S-phân b/ ng 0ng áp trong m t c"t PK 1+40

I - Bi4u5 phân b/gradien thmJx theo tr7c c8amàng ch/ng thm.

Hình 3: S-phân b/ ng 0ng áp trong m t c"t PK 3+91

I- ng bão hòa trong n?np;

II- Bi4u5 phân b/gradient thmJx theo tr7c c8amàng ch/ng thm.



273.0

250.0

1:2



255.0



235.0



220.0



1:2

1:2 1:2



230.0

1:2

270.0

MNGC

6.0

9.0

22.0

20.4

25.0

200.00 199.0



18.0

9.0

150.00

120.0



1:3 1:2

210.0



40000

100.00

50.00

50 0.0 .0300 0 350 0.00 0150 0.02.000 2.0

0.00 50 1000.0

0.0



MNGC 270.0



1:3

251.0



235.00

.0251

1:3

4.1



9.0 181.00

200.00



1:2

3.5



1.7 120.00

150.00



150.00

.0250 0002.00 40000

350 0.0300 0.0

100.00

0.00 100.00050.0 0150.0

273.0



Ảnh hưởng của hệ số đất thấm ở đất thân và nền đập lên các thông số dòng thấm

Chủ đề:

Tài liệu liên quan

Tài liêu mới

AI tóm tắt

Giới thiệu tài liệu

Đối tượng sử dụng

Từ khoá chính

Nội dung tóm tắt

Hỗ trợ

Phương thức thanh toán

Theo dõi chúng tôi