PHẠM Đỗ Chung-HNUE-2020
Bồi dưỡng giáo viên giảng dạy
Khoa học tự nhiên THCS
Phạm Đỗ Chung
Bộ môn Vật lí chất rắn – Điện tử
Khoa Vật lí, ĐH Sư Phạm Hà Nội
136 Xuân Thủy, Cầu Giấy, Hà Nội
Khoa học tự nhiên THCS
ÂM THANH
PHẠM Đỗ Chung-HNUE-2020
Chương 1: Cơ sở về dao động, sóng cơ và sóng âm
1. Cơ sở về dao động
2. Sóng cơ trên một sợi dây kéo căng
2
PHẠM Đỗ Chung-HNUE-2020 3
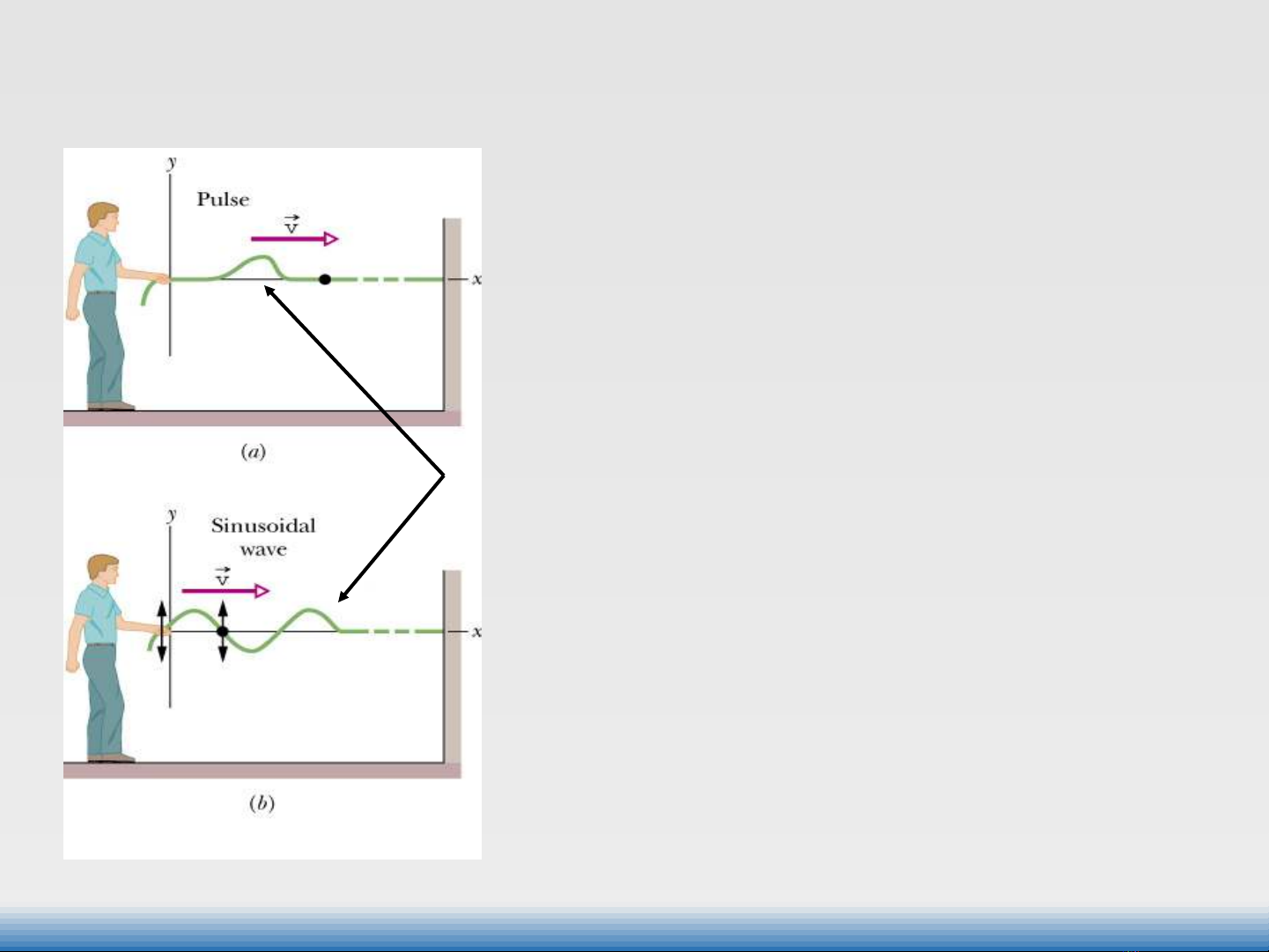
Sóng ngang
Độ dịch chuyển (li độ) của các phần trên sợi dây vuông
góc với phương truyền sóng.
Dạng sóng
tùy vào nguồn sóng
Sóng cơ trên một sợi dây kéo căng
PHẠM Đỗ Chung-HNUE-2020 4
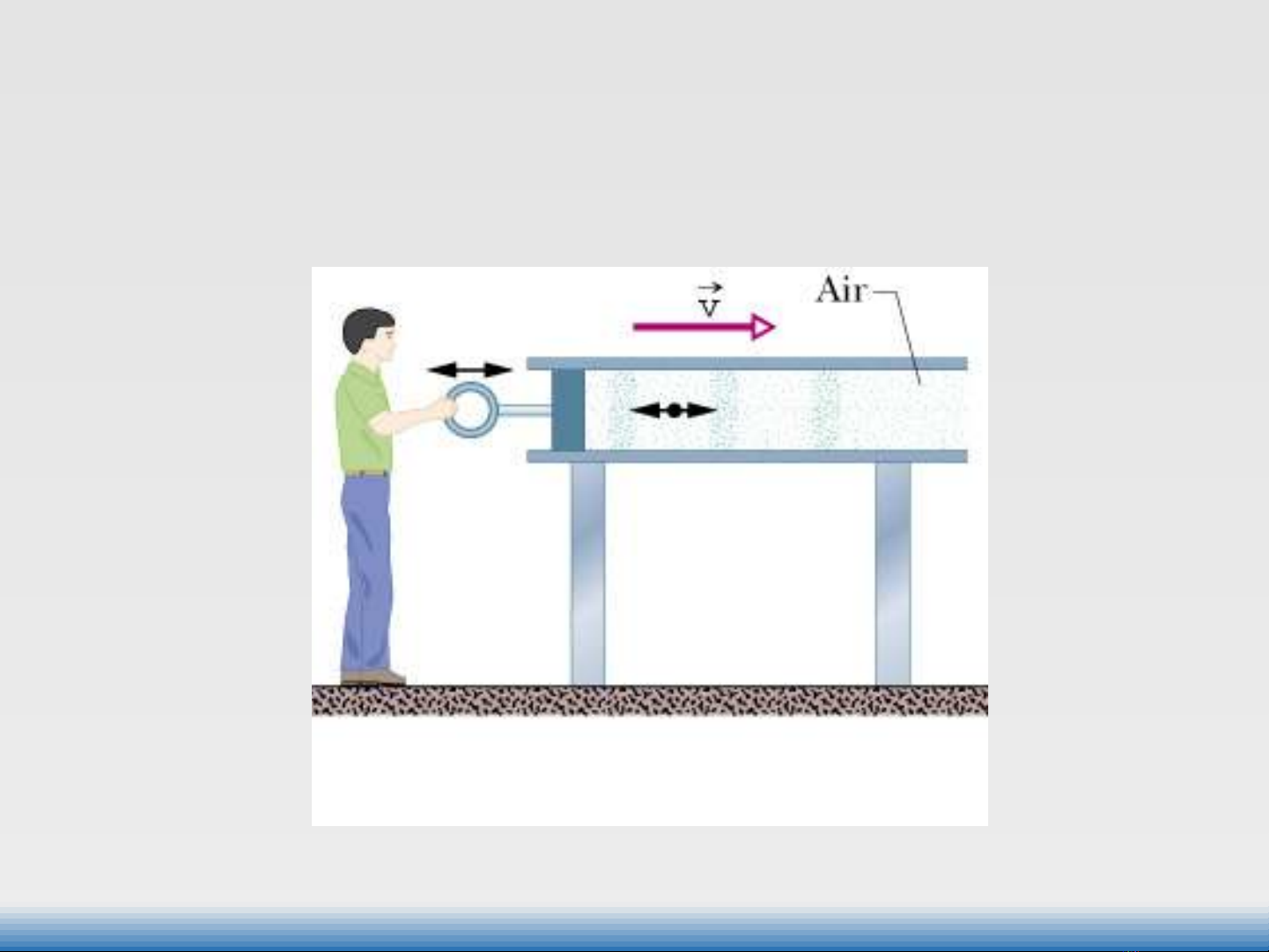
Fig. 16-2
Sóng dọc
Độ dịch chuyển (li độ) của các phần tử vật chất của môi trường truyền sóng song
song với phương truyền sóng.
PHẠM Đỗ Chung-HNUE-2020 5
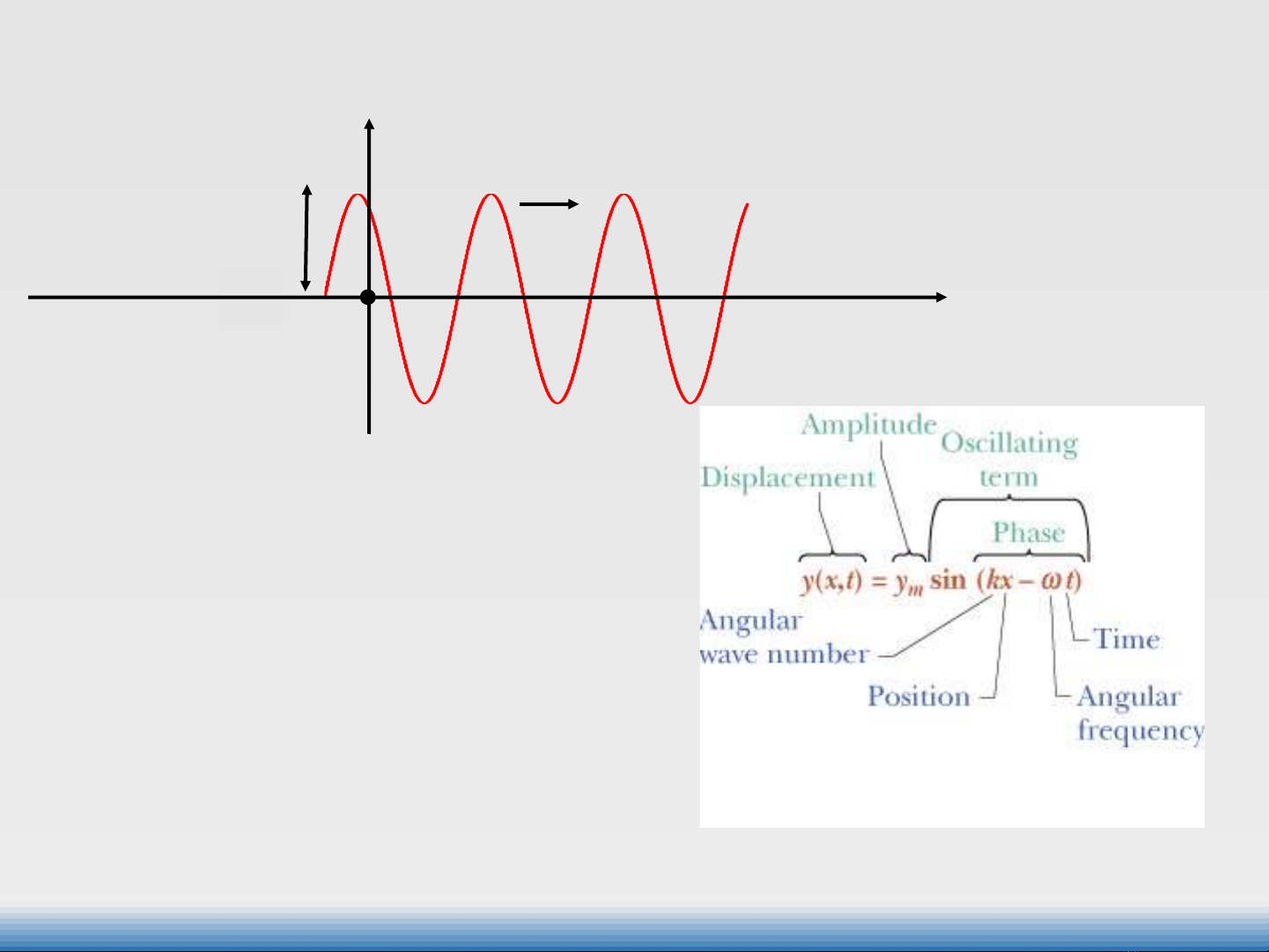
Hình 17-4
Phương trình sóng và một số đặc trưng củasóng
sin t
80
t
v
m
y
x
( ) ( )
,sin
m
yxt y kx t
w
=-
y
Sự lan truyền một sóng ngang
Displacement (y): li độ của sóng
Amplitude (ym): biên độ sóng
Oscillating term: thừa số dao động
Phase: pha của sóng
Angular wave number (k): số sóng
Position tọa độ (vị trí) của
phần tử dao động
Angular frequency: tần số góc
Time: thời gian