Cấu trúc dữliệu và Giải thuật
Đỗ Bích Diệp - Khoa CNTT - ĐHBKHN 1
CấutrúcdữliệuvàGiảithuật
Chương V: Đồ thị(phần2)
Cây và Rừng trong lý thuyếtđồ thị
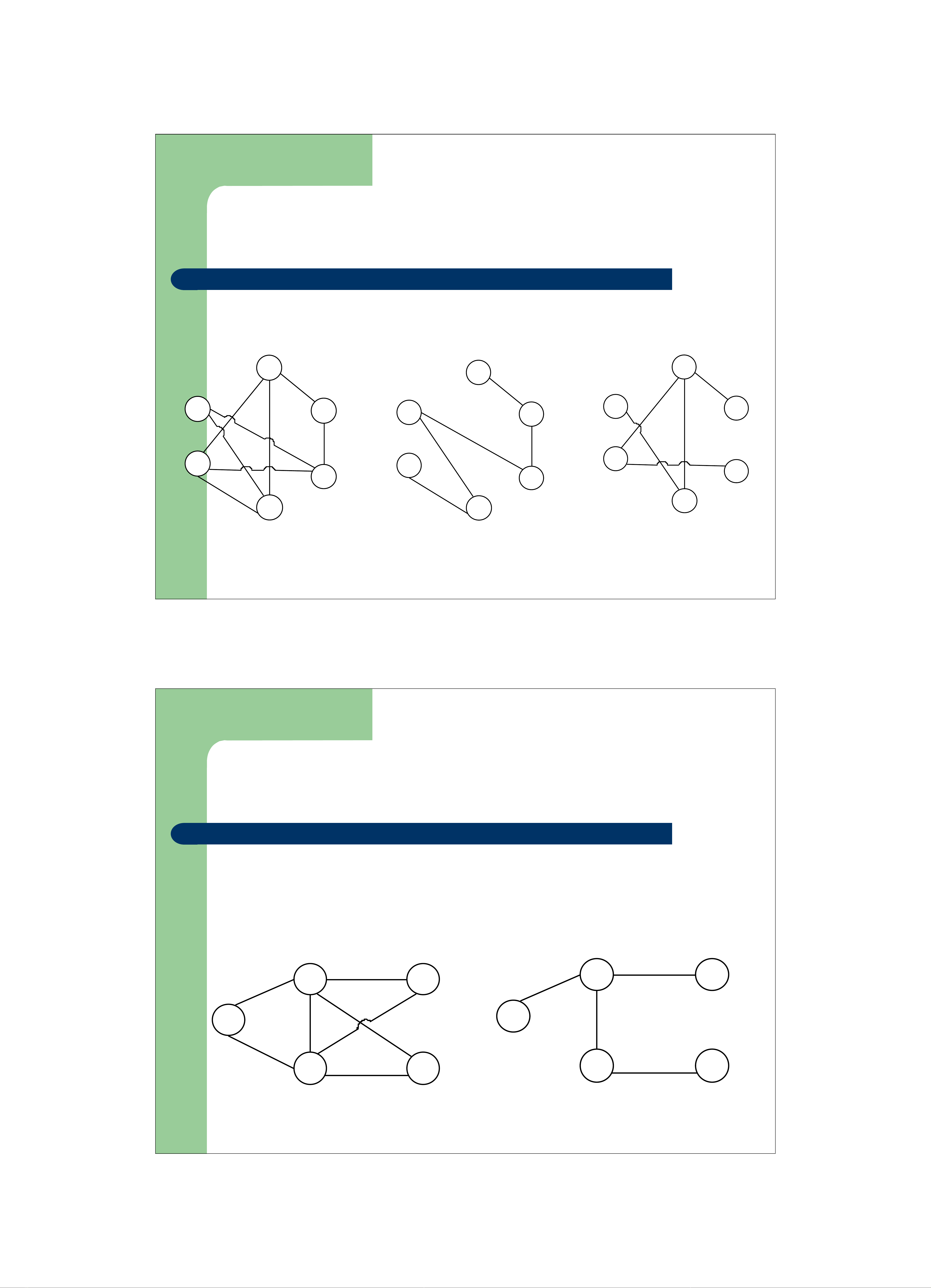
–Cây
zMộtđồ thịvô hướng liên
thông
zKhông có chu trình
–Rừng
zMộttậpcáccâyphân
biệt
Cây
Rừng
Cấu trúc dữliệu và Giải thuật
Đỗ Bích Diệp - Khoa CNTT - ĐHBKHN 2
Cây khung
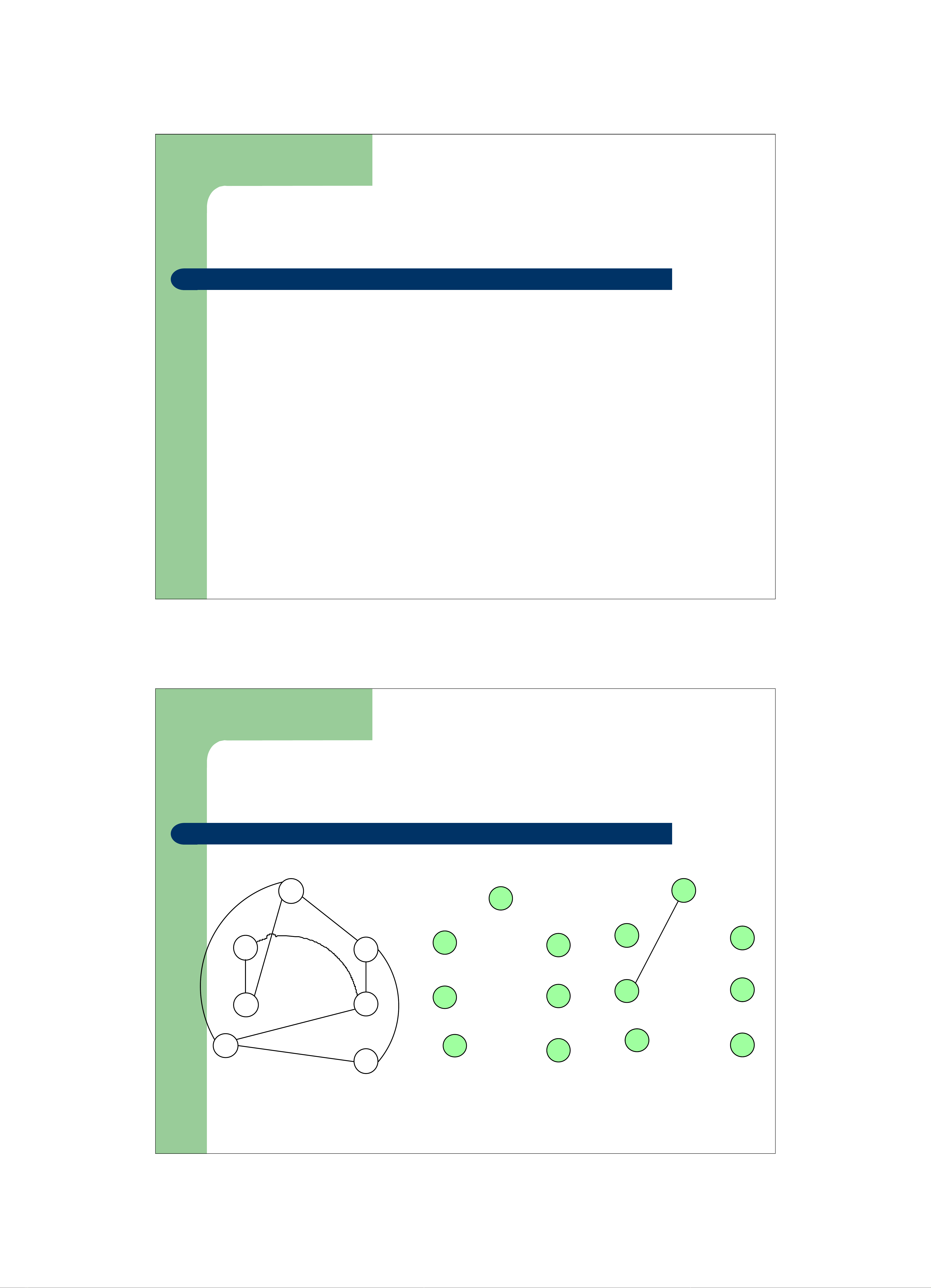
–Cho mộtđồ thịvô hướng, liên thông G
zCây khung trên G là cây có chứatấtcảcác đỉnh trong G
1
23
6
5
4
1
23
6
5
4
1
23
6
5
4
Đồ thịCây khung Cây khung
Bài toán tìm cây khung cựctiểu
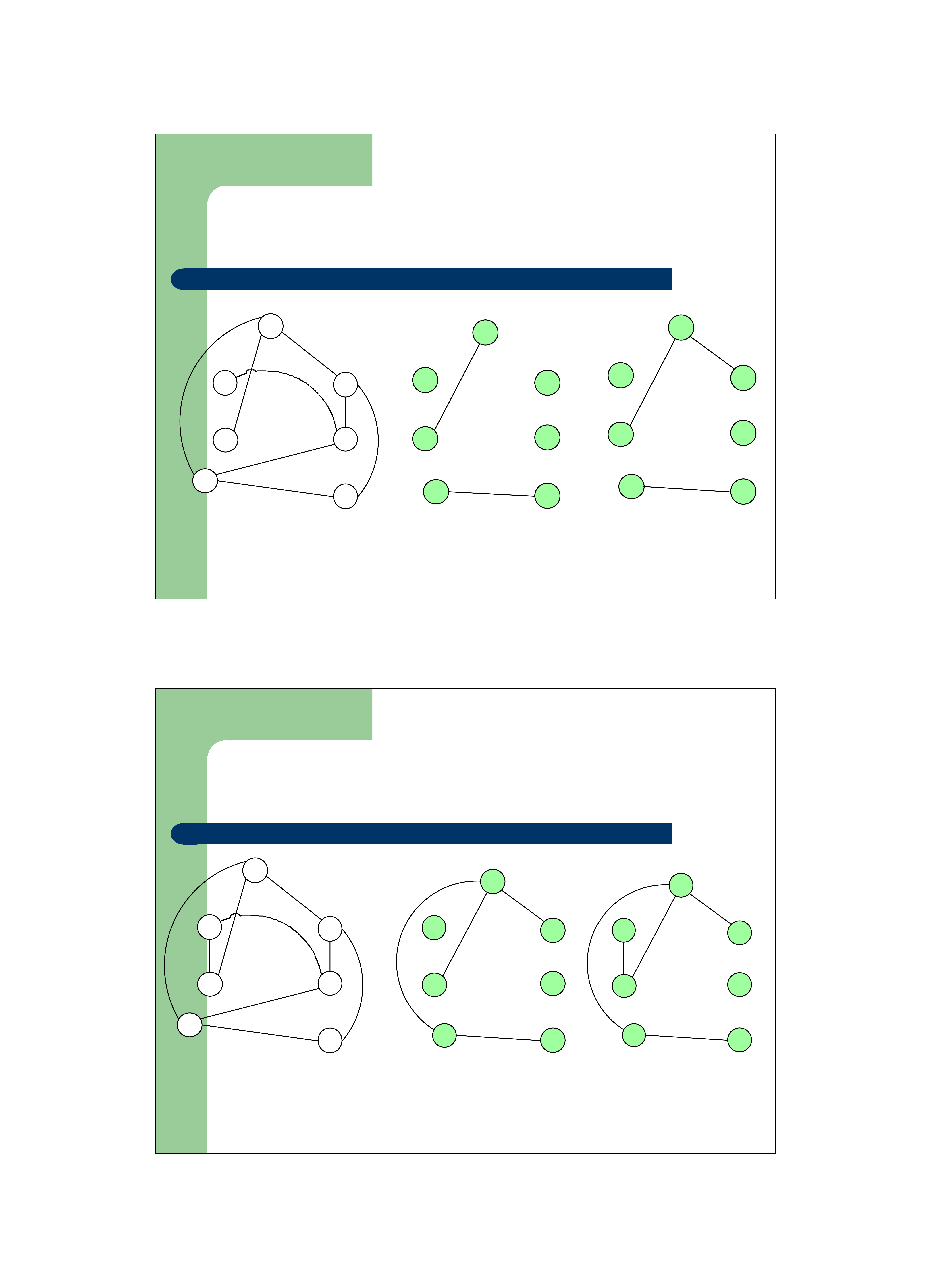
zCho mộtđồ thịvô hướng, liên thông có trọng số
zGiá trịcủamột cây khung là tổng trọng sốcủacáccung
trong cây
zTìm một cây khung vớigiátrịnhỏnhấttrênđồ thị
5
10
6
2
4
8
9
5
6
2
4
Đồ thịđầuvào Cây khung cựctiểu
Cấu trúc dữliệu và Giải thuật
Đỗ Bích Diệp - Khoa CNTT - ĐHBKHN 3
Giảithuật Kruskal - MST
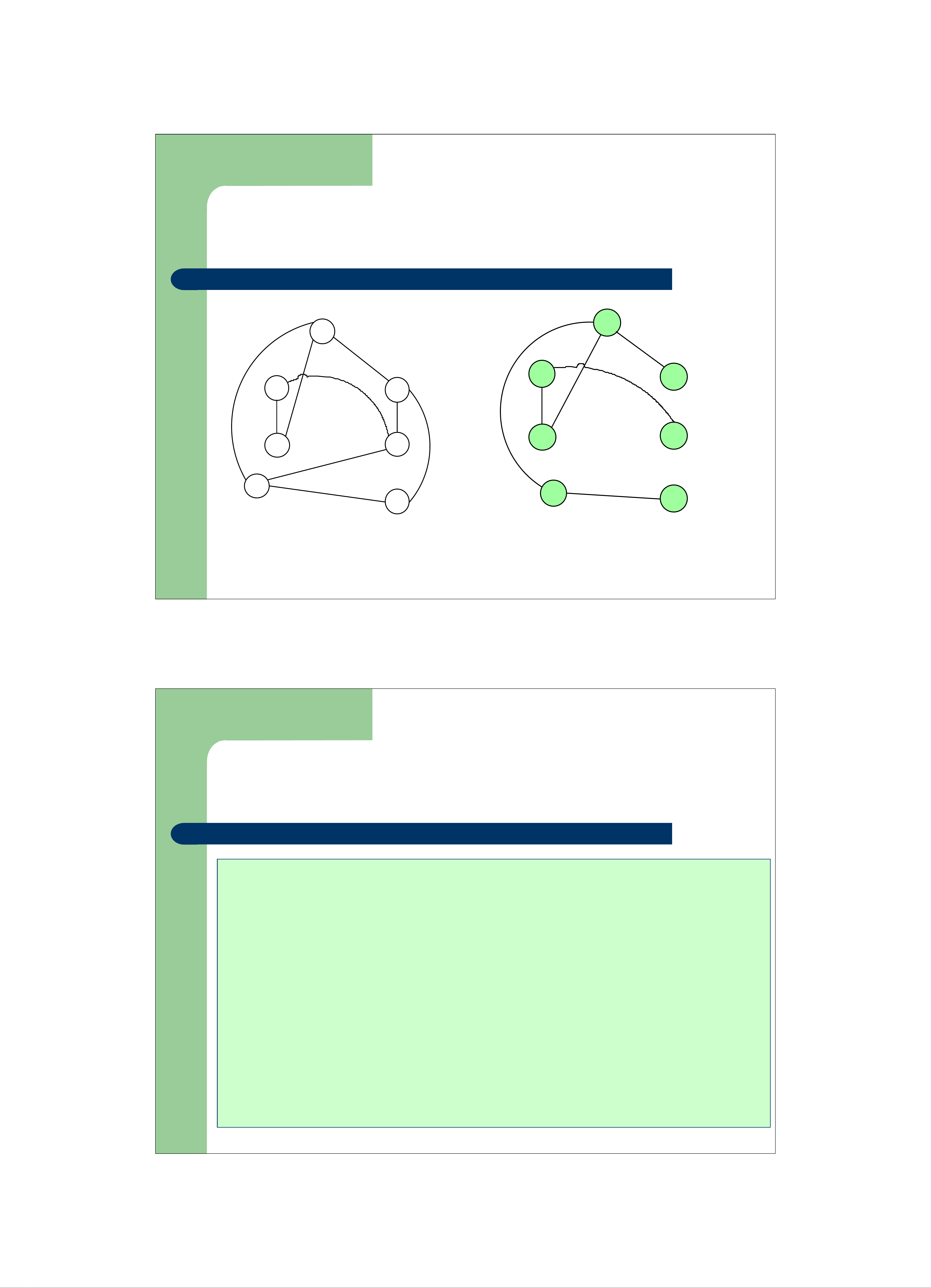
zÝ tưởng
–Lầnlượt thêm vào cây khung cần tìm các cung có
trọng sốnhỏnhấtcóđượctạimộtthờiđiểmnếu
cung đó không tạothànhchutrìnhtrênphầncây
khung đang tạmcó
Giảithuật Kruskal-MST
1
23
6
5
4
7
7
14
3
7
10
8
12
10
16
Đồ thịban đầu
1
23
6
5
4
7
Bước1
1
23
6
5
4
7
3
Bước2
Cấu trúc dữliệu và Giải thuật
Đỗ Bích Diệp - Khoa CNTT - ĐHBKHN 4
Giảithuật Kruskal – MST
1
23
6
5
4
7
3
7
1
23
6
5
4
7
3
7
7
Bước4Bước3
1
23
6
5
4
7
7
14
3
7
10
8
12
10
16
Đồ thịban đầu
Giảithuật Kruskal - MST
1
23
6
5
4
7
3
7
7
810
Bước6
1
23
6
5
4
7
3
7
7
8
Bước5
1
23
6
5
4
7
7
14
3
7
10
8
12
10
16
Đồ thịban đầu
Cấu trúc dữliệu và Giải thuật
Đỗ Bích Diệp - Khoa CNTT - ĐHBKHN 5
Giảithuật Kruskal - MST
1
23
6
5
4
7
3
7
7
810
10
Bước7-
Cây khung cựctiểu
1
23
6
5
4
7
7
14
3
7
10
8
12
10
16
Đồ thịban đầu
Giảithuật Kruskal-MST
Algorithm KRUSKAL(G) {đồ thị G có n đỉnh}
1. {Khởi tạo các cụm ban đầu, mỗi cụm chứa 1 đỉnh của đồ thị }
for each vertex v in G do C(v) ←{v}.
2. Khởi tạo một Queue Q chứa các cung trong G, sắp xếp theo chiều tăng dần của trọng
số.
3. {Khởi tạo cây khung ban đầu rỗng} T ←∅
4. {Lần lượt xét các cung đưa vào trong cây khung cần tìm}
while T chứa ít hơn n-1 cung do begin
Lấy ra từ Q cung (u,v) có trọng số nhỏ nhất
C(v) là cụm chứa v, C(u) là cụm chứa u.
if C(v) ≠C(u) then begin
T = T U {(u,v)}
Nhập C(u) với C(v)
end
end
return T