intTypePromotion=1
zunia.vn Tuyển sinh 2024 dành cho Gen-Z zunia.vn zunia.vn
ADSENSE
 » 
 » 

Bài giảng Cơ học chất: Chương 8 - PGS.TS. Lê Song Giang

Chia sẻ: _ _ | Ngày: | Loại File: PDF | Số trang:19

Thêm vào BST
Báo xấu
7
lượt xem 2
download
 
  Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng Cơ học chất - Chương 8 Lớp biên-lực cản-lực nâng, cung cấp cho người học những kiến thức như: khái niệm lớp biên; Phương trình lớp biên; Hệ thức tích phân Karman; Tính toán lớp biên trên tấm phẳng với Hệ thức tích phân Karman; Lớp biên rối;... Mời các bạn cùng tham khảo!

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Cơ học chất: Chương 8 - PGS.TS. Lê Song Giang

  1. CHƯƠNG 8 LỚP BIÊN – LỰC CẢN – LỰC NÂNG 1. Lớp biên. 2. Lực cản & Lực nâng. 143
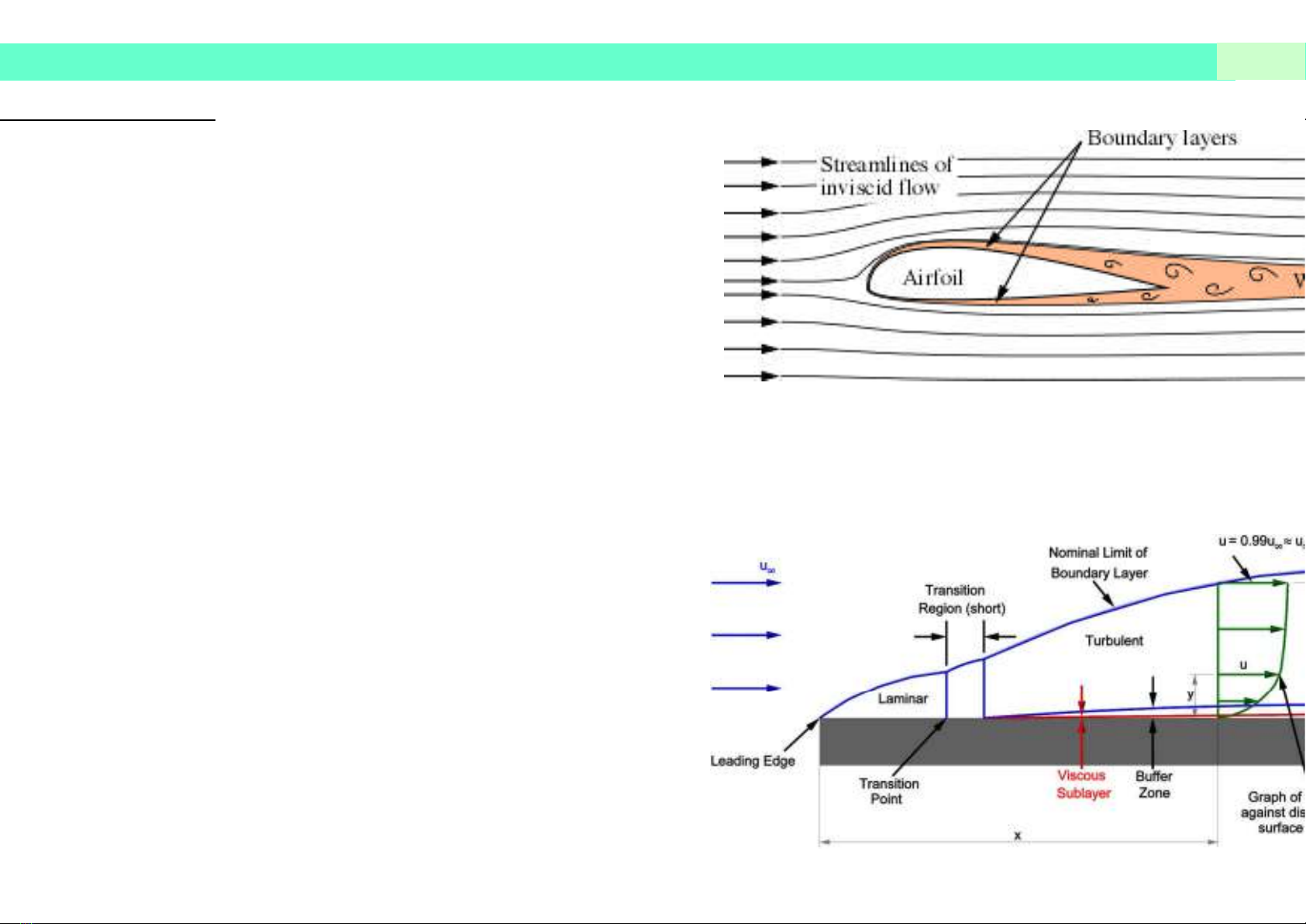
  2. . LỚP BIÊN (1/7) Pgs.Ts .1 Các khái niệm. Khi lưu chất chuyển động bao quanh một vật thể, hiệu ứng nhớt chỉ tồn tại trong một phạm vi hẹp gần sát bề mặt vật thể. Phần lớn môi trường còn lại ở cách xa vật có thể được coi là không nhớt. Lớp biên: lớp lưu chất chuyển động trong khoảng từ bề mặt vật thể tới vị trí có vận tốc bằng 99% vận tốc dòng tự do. Phân loại: • Lớp biên tầng: Rex ≤ 3.105 • Lớp biên chuyển tiếp • Lớp biên rối: Rex ≥ 3.105 - 5.105 • Lớp biên tầng ngầm 144
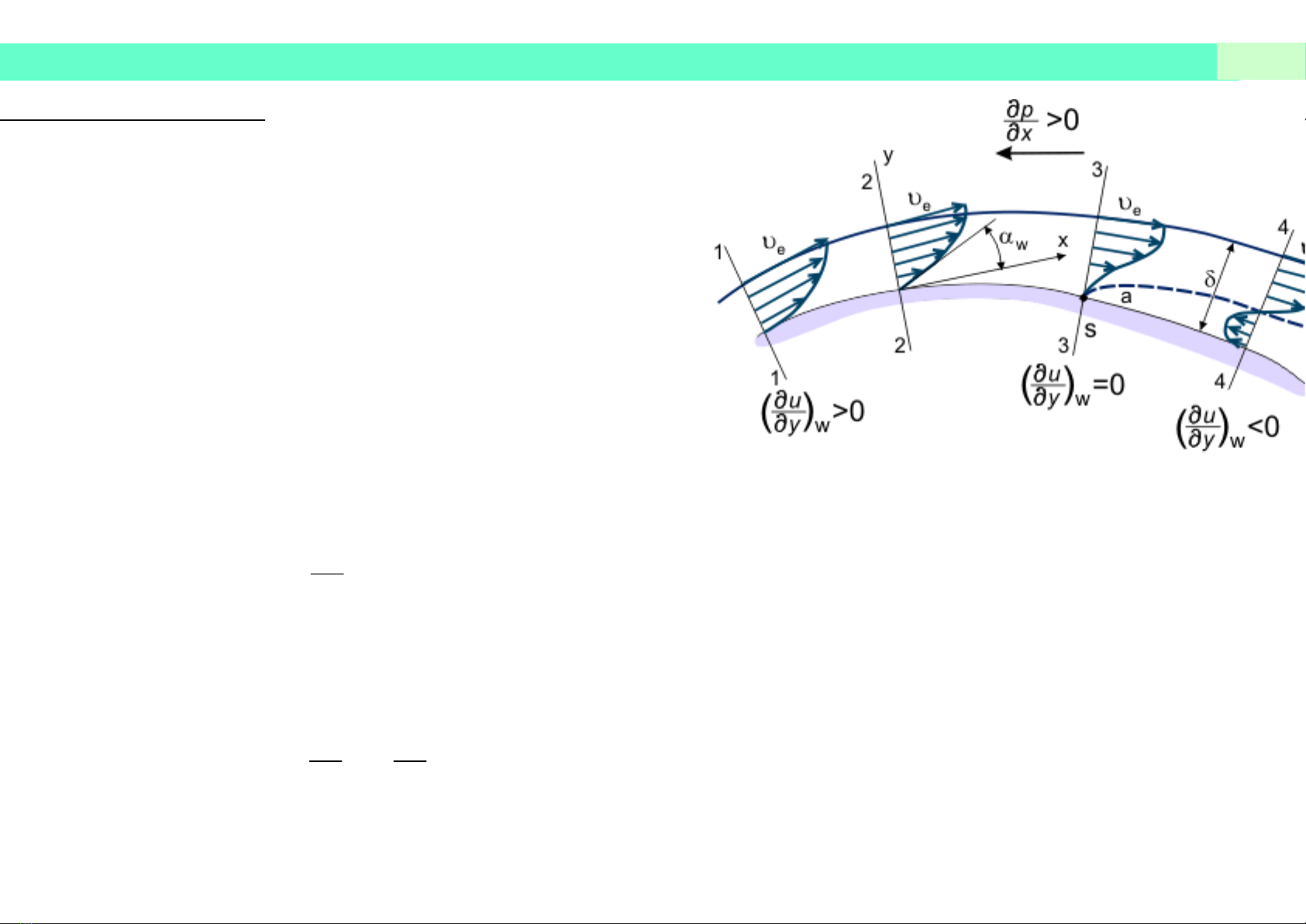
  3. 1. LỚP BIÊN (2/7) Pgs.Ts 1.1 Các khái niệm (tt). Hiện tượng tách rời lớp biên. Các bề dày: - Bề dày lớp biên: δ - Bề dày dịch chuyển: δ*  *  u     1  dy  u  0    - Bề dày động lượng: δi  u  u  i   1  dy  u  u 0     145
  4. . LỚP BIÊN (3/7) Pgs.Ts .2 Phương trình lớp biên (pt Prandtl). Chuyển động 2D, ổn định của lưu chất không nén được, bỏ qua lực khối Lớp biên:     L => v  u và  x y Phương trình Navier-Stokes => Phương trình lớp biên Prandtl  u v  u v   0  x  y  0  x y   u u 1 p   2u  2u   u u 1 p  2u  u v    2  2  => u v   2  x y  x  x y     x y  x y  v   2v  2v   p u  v v 1 p  0    2  2   x  y  y  x y     y Gradient áp suất =? Pt Bernoulli => 1 p u   u   x x Trường hợp lớp biên trên tấm phẳng: u u u  2u 0 => u v  2 x x y y 146
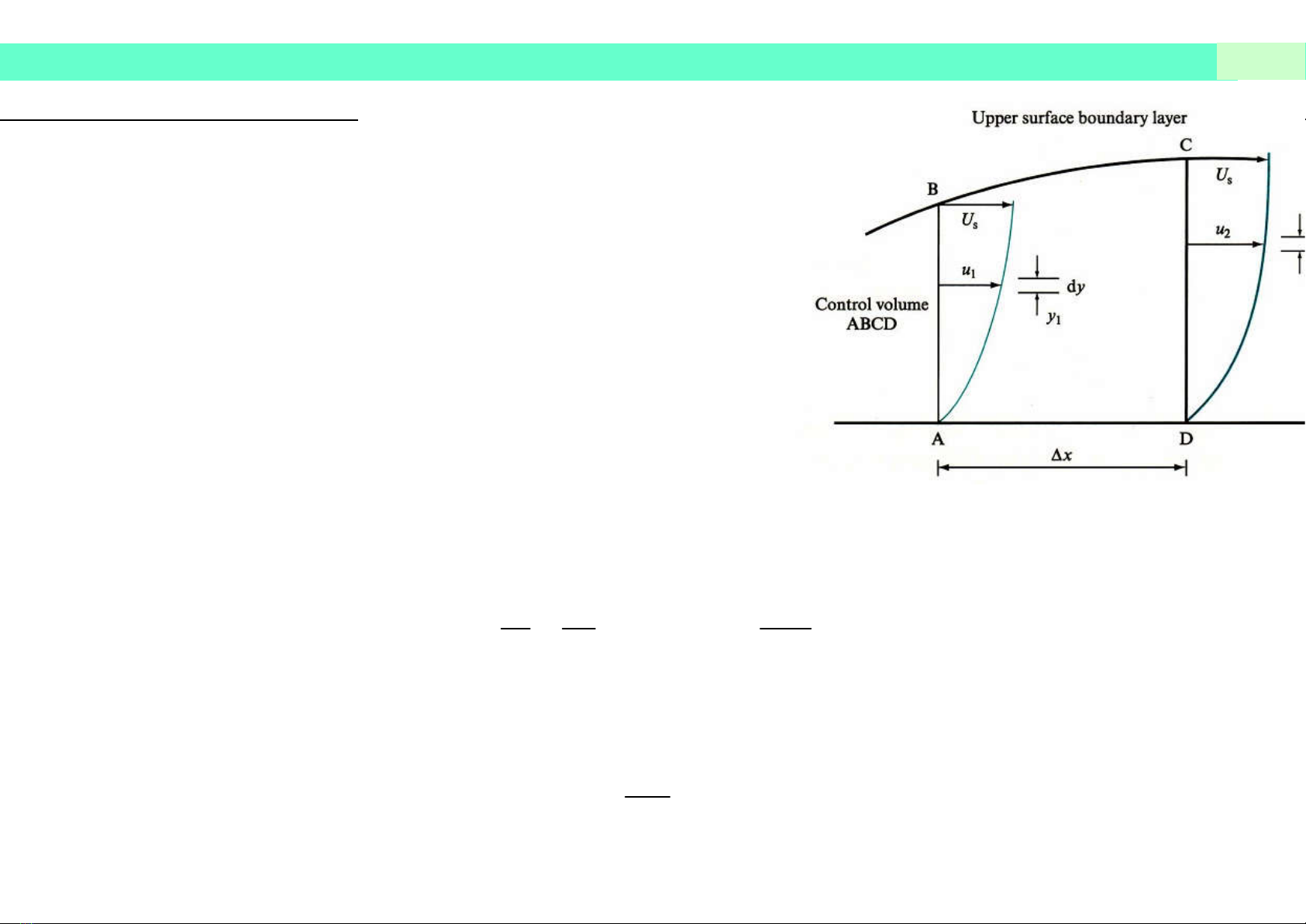
  5. 1. LỚP BIÊN (4/7) Pgs.Ts .3 Hệ thức tích phân Karman Thể tích kiểm soát ABCD Áp dụng phương trình biến thiên động lượng cho thể tích kiểm soát cho kết quả: 0 d du   i u    *u  2  dx dx Trường hợp lớp biên trên tấm phẳng 2 d i  0  u dx 147
  6. . LỚP BIÊN (5/7) Pgs.Ts .4 Tính toán lớp biên trên tấm phẳng với Hệ thức tích phân Karman Do trong pt có số hạng δi nên phép giải phải dựa trên giả thiết phân bố vận tốc 1.4.1 Lớp biên tầng Giả thiết profile vận tốc 3 u 3 y 1 y      => Bề dày động lượng:  i  0.1393 u 2    2    du u Ứng suất ma sát: 0    1 .5  dy y 0  Thay vào hệ thức tp Karman: 2 d i u 0.1393d   0  u  => 1 .5   u2  =>  4,64 Re 1/ 2 x dx  dx x Hệ số ma sát cục bộ: 0 cf   0.646 Re 1/ 2 x 1 2 u 2 Hệ số ma sát: L Cf    dx 0 0  1.292 Re 1/ 2 L 1 2 u L 148 2
  7. . LỚP BIÊN (6/7) Pgs.Ts .4.2 Lớp biên rối Giả thiết profile vận tốc 1/ 7 u  y  i  0.0972   => u    1/ 2 Ứng suất ma sát: Blasius 2    0  0.0225 u  u       Thay vào hệ thức tp Karman: 1/ 2 d i    0.0972 d   0  u 2 => 0.0225 u  2   u2 =>  0,371 Re 1/ 5 dx  u     dx x x    Hệ số ma sát cục bộ: 0 cf   0.0576 Re 1/ 5 x 1 2 u  2 Hệ số ma sát: L Cf   0 0 dx  0.074 Re 1/ 5 L 1 2 u  L 149 2
  8. . LỚP BIÊN (7/7) Pgs.Ts Ví dụ: Một tấm phẳng 0,8 x 1,2m rơi thẳng đứng trong không khí theo chiều dọc. Biết trọng lượng củ phẳng là G=60N. Bỏ qua bề dày của tấm phẳng, hỏi vận tốc rơi của nó. Giải Khi vận tốc rơi của tấm phẳng đạt tới giá trị ổn định, trọng lượng của tấm phẳng cân bằng với lực ma sát: 1 Fms  G  C f V 2 L.b.2  G 2 Giả thiết lớp biên trên tấm phẳng ở trạng thái chảy rối: 1 / 5 5/9  VL   G  C f  0,074 Re 1/ 5 L  0,074  V 2 L.b  G V    0,074  1/ 5 L4 / 5 .b       Thay số: 5/9  60 N  V    132,2 m s    0,074.1,228 kg m 3 0,15.10  4 m 2 s 1,2m  0,8m  1/ 5 4/5  Kiểm tra giả thiết: V .L 132,2 m s .1,2m Re L   4 2  1,06.107 => Giả thiết đúng 150  0,15.10 m s
  9. . LỰC NÂNG, LỰC CẢN (1/7) Pgs.Ts .1 Khái niệm Lực tác dụng lên vật thể chuyển động trong Lưu chất : – Áp lực – Lực ma sát Phân tích theo hiệu quả tác động: • Lực cản: cùng phương với c.động 1 2 FD  u C D A 2 • Lực nâng: vuông góc với phương c.động 1 2 FL  u  C L A 2 151
  10. . LỰC NÂNG, LỰC CẢN (2/7) Pgs.Ts .2 Lực cản: Lực cản ma sát: lực tác dụng lên tấm phẳng hoặc vật có dạng lưu tuyến đặt song song với vector vận tốc Lực cản áp suất: lực tác dụng lên tấm phẳng đặt vuông góc với vận tốc Lực cản hình dạng = Lực cản ma sát + Lực cản áp suất Lực cản sóng 152
  11. . LỰC NÂNG, LỰC CẢN (3/7) Pgs.Ts 153
  12. . LỰC NÂNG, LỰC CẢN (4/7) Pgs.Ts 154
  13. . LỰC NÂNG, LỰC CẢN (5/7) Pgs.Ts .3 Lực nâng: Chênh lệch áp suất trên 2 mặt Cấu trúc dòng chảy 155
  14. 2. LỰC NÂNG, LỰC CẢN (6/7) Pgs.Ts • Các hệ số lực được xác định bằng thực nghiệm 156
  15. 2. LỰC NÂNG, LỰC CẢN (7/7) Pgs.Ts y Ví dụ: Có một trụ điện hình nón cụt cao H=16m, đường kính dưới chân d là D=1,2m và đường kính trên đỉnh là 0,8m. Gió thổi ngang qua trụ u điện với vận tốc biến thiên theo chiều cao: 1/ 7 Di  y u  u0   H  dy y Với u0=12m/s. Hỏi lực của gió tác động lên trụ điện Giải D Xét một đoạn trụ điện có chiều cao dy vô cùng nhỏ ở độ cao y. Xem đoạn trụ điện dy là hình trụ trò đường kính bằng đường kính trung bình: y 1 1 Di  D  D  d   dFD  u 2C D A  u 2C D Di dy H 2 2 2 1   y 1/ 7   y  dFD   u0    C D  D  D  2  H     H Lực cản của trụ điện: 1 2  7 7  d  FD   dFD  u0 C D D.H   1     1255,1N H 2  9 16  D   157
  16. CÁC TOÁN TỬ Pgs.Ts Toán tử Napla:        i  j k x y z Các toán tử: p  p  p  . p  grad  p   i j k x y z   u x u y u z .u  divu     x y z    i j k        u  rot u   x y z ux uy uz 2 2 2 2 .      2  2  2 x y z 158
  17. ĐẶC TRƯNG HÌNH HỌC CỦA MỘT SỐ HÌNH PHẲNG Pgs.Ts 159
  18. CÁC CÔNG THỨC TOÁN Pgs.Ts Chuỗi Taylor: df  x  d 2 f  x  x 2 f  x  x   f  x   x  2  ... dx dx 2! Công thức Gauss:   . AdV   A.ndS (A là hàm vô hướng hoặc có hướng) V S 160
  19. CÁC CÔNG THỨC TOÁN Pgs.Ts Kích thước hình học của một số mặt cắt 161
ADSENSE

CÓ THỂ BẠN MUỐN DOWNLOAD

THÔNG TIN
TRỢ GIÚP
HỖ TRỢ KHÁCH HÀNG
Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.

 

Đồng bộ tài khoản
9=>0