CƠ HC MÔI TRNG LIÊN TC
TS. PH
M V
N
T
76
Chng 3: TRNG THÁI BIN DNG
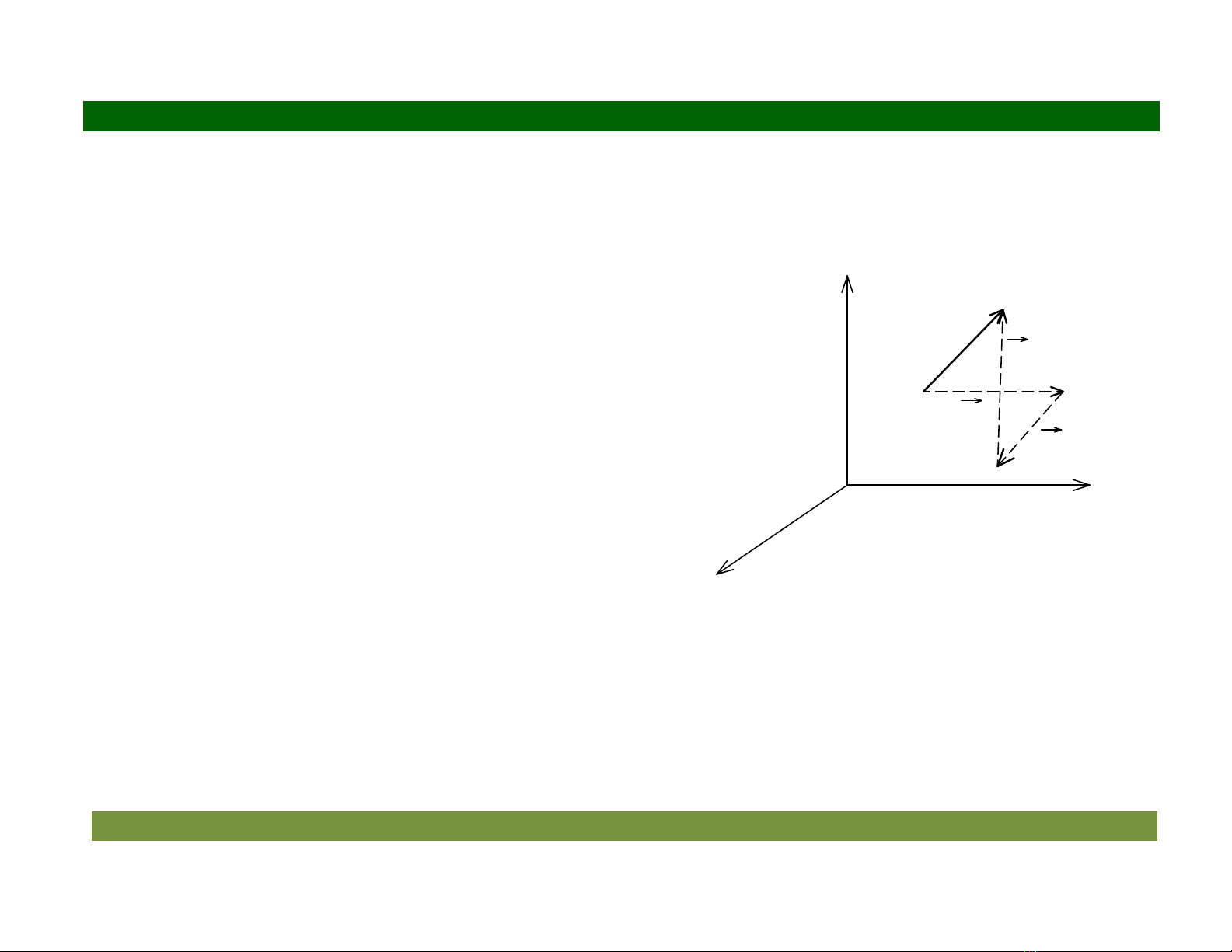
3.1 Khái nim chuyn v$
Xét m"t vt th àn hi, ti thi im ban %u
0
t t
=
, vt th cha bin dng. Gi s& ti m"t
im bt k# M trong vt th, trong h ta "
1 2 3
ox x x
là:
(
)
1 2 3
M x , x , x
. D i tác dng ca
ngoi lc làm vt th b bin dng và im M
dch chuyn sang v trí m i là M’ có ta "
(
)
1 2 3
M ' x ' , x ' , x '
.
MM'
$c gi là chuyn v ca
im M.
Ta có:
1 2 3
MM' u u u
= + +
Hình 3.1

CƠ HC MÔI TRNG LIÊN TC
TS. PH
M V
N
T
77
trong ó:
'
1 1 1
'
2 2 2
'
3 3 3
u x x
u x x
u x x
= −
= −
= −
(3.1)
Các thành ph%n chuyn v u, v, w là các hàm ta " ca im:
1 1 1 2 3
2 2 1 2 3
3 3 1 2 3
u f (x , x , x )
u f (x , x , x )
u f (x , x , x )
=
=
=
(3.2)
Chuyn v toàn ph%n ca im M:
2 2 2
1 2 3 1 2 3
u u u F(x ,x ,x )
δ = + + =
(3.3)
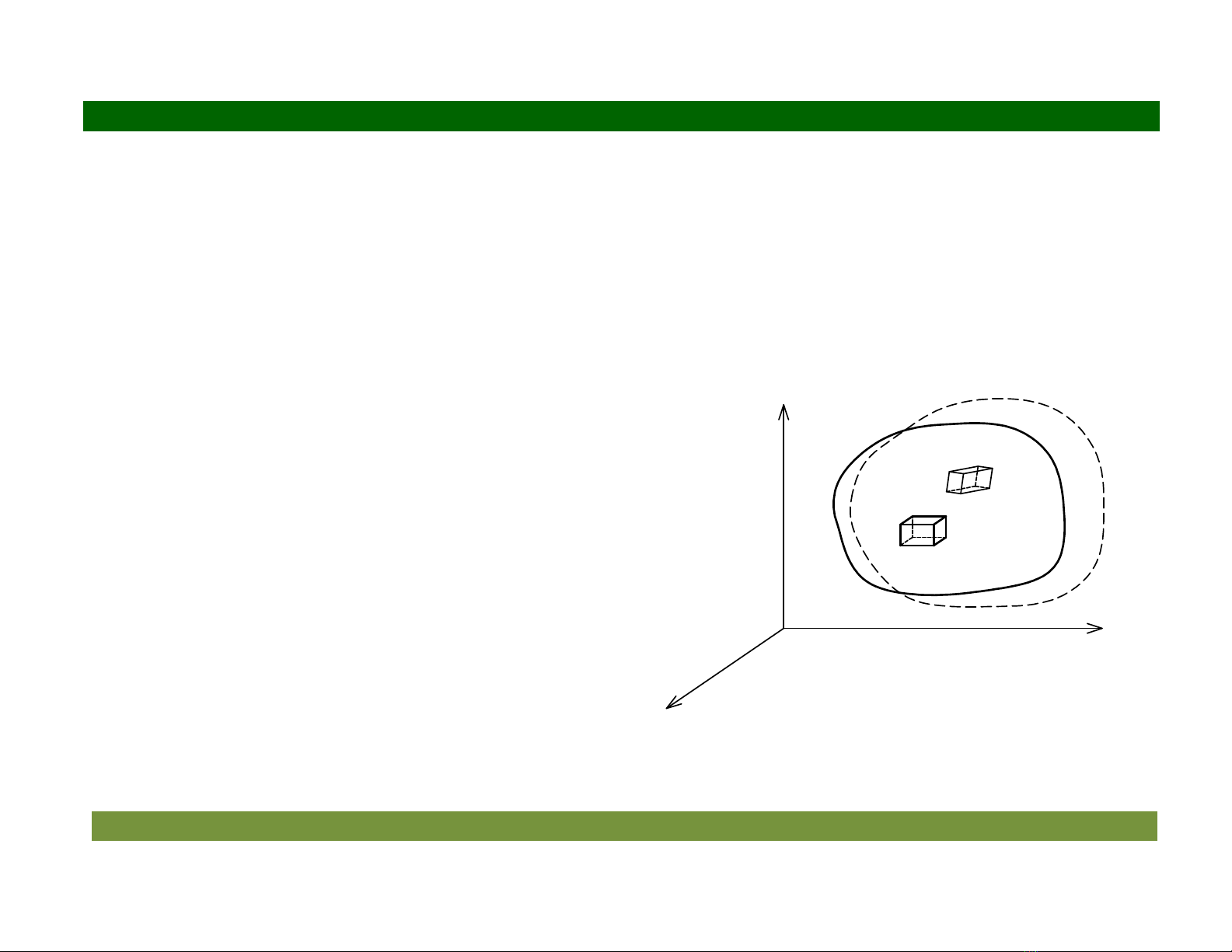
3.2 Khái nim bin dng
Ti im M trong vt th, tách m"t phân t hình h"p có các mt song song v i các mt
ta " (hình 3.2). Khi vt th bin dng thì phân t s chuyn sang v trí m i, nu gi
CƠ HC MÔI TRNG LIÊN TC
TS. PH
M V
N
T
78
thuyt phân t không bin dng, xác nh v trí m i ca phân t thì ch3 v i 3 thành ph%n
chuyn v ti im M cha vì hình h"p ch nht có th quay quanh cnh MN ( song
song v i trc
1
x
) hoc cnh MP ( song song v i trc
2
x
) hoc cnh MR ( song song v i
trc
3
x
) hoc trc bt k# không song song v i các trc ta ", lúc ó c%n phi k n 3
thành ph%n góc xoay. Nhng thành ph%n này
$c gi là các thành ph%n xoay cng, ký
hiu
23
ω
( quay quanh trc
1
x
);
31
ω
( quay
quanh trc
2
x
);
12
ω
( quay quanh trc
3
x
).
Trng h$p c bit nu
12 23 31
0
ω = ω = ω =
ngh!a là không có s quay ti im kho sát,
thng $c gi là bin dng thu%n túy.
Hình 3.2
!
!
CƠ HC MÔI TRNG LIÊN TC
TS. PH
M V
N
T
79
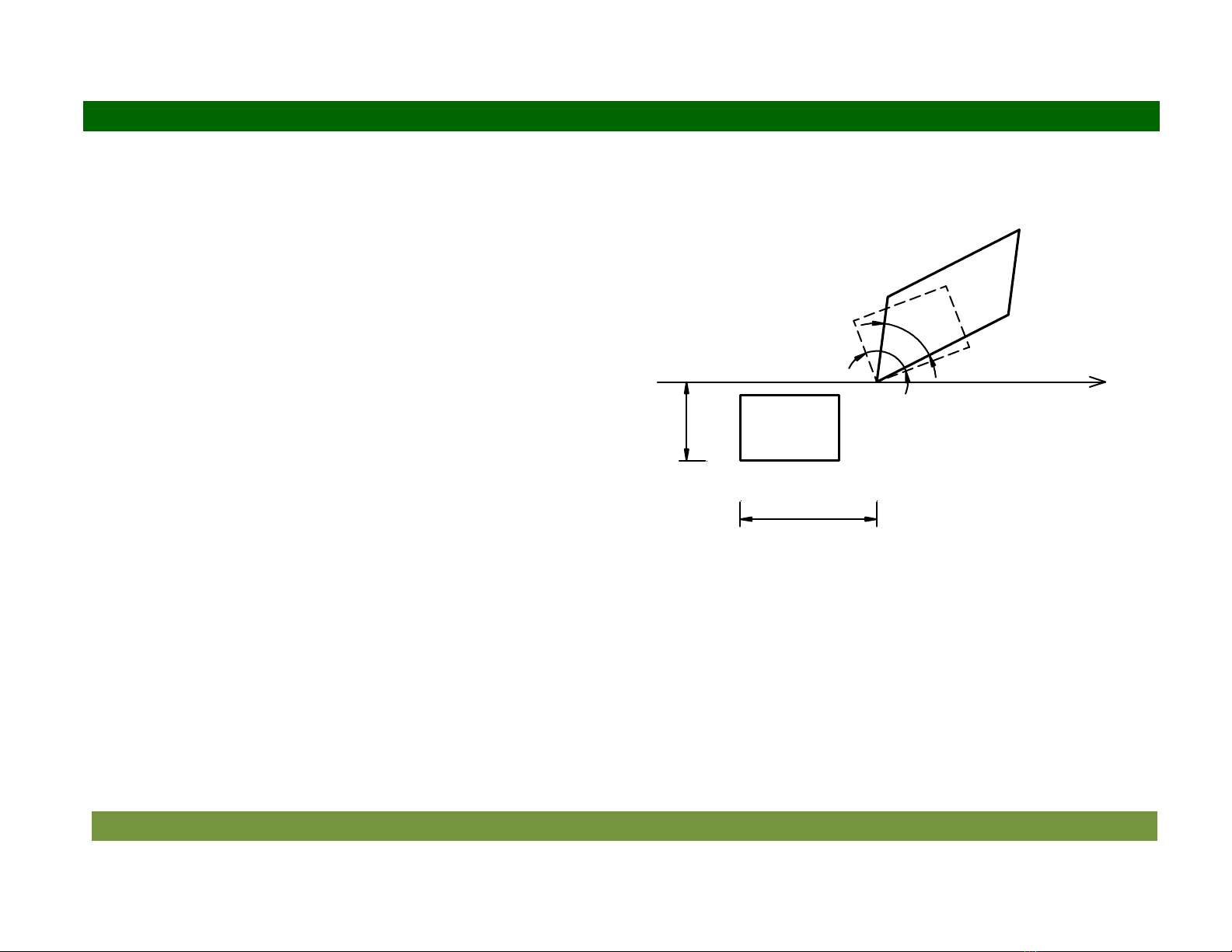
Khi phân t b bin dng thu%n túy thì
các cnh b bin dng dài, góc vuông b thay
i gi là bin dng góc. Trên hình v 3.3
biu di-n hình chiu ca phân t trên mt
1 2
Ox x
. V trí ban %u là (MNP), sau khi
bin dng thì v trí là
1 1 1
(M N P )
.
Hình 3.3
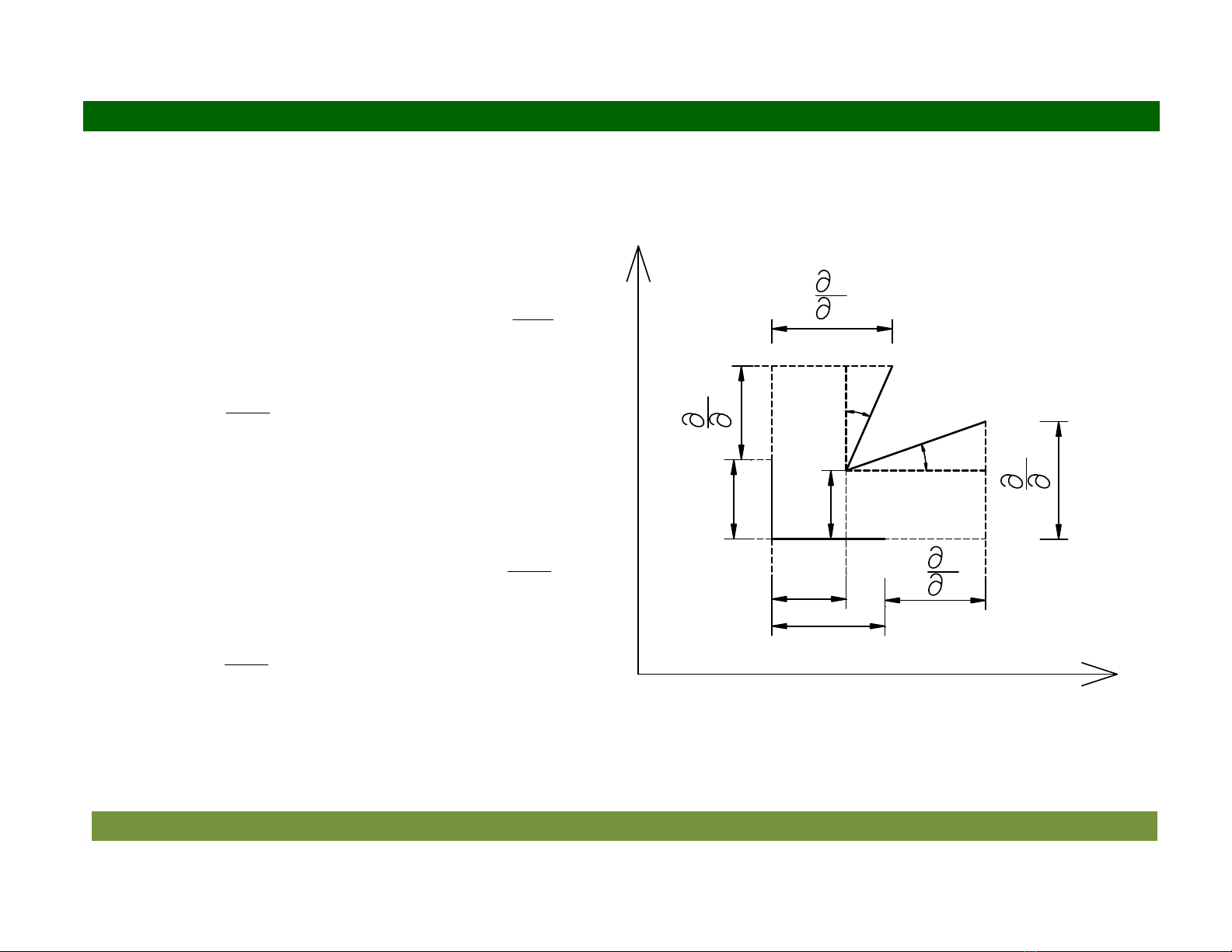
3.3 Quan h vi phân gi1a chuyn v$ và bin dng bé
Xét phân t MNP sau khi bin dng tr thành phân t
1 1 1
M N P
, ti im
1 2
M (x , x )
chuyn v tng ng là:
1 1 2
u (x ,x );
2 1 2
u (x ,x )
.
u
90°
90 - γ
!
!
!
v
CƠ HC MÔI TRNG LIÊN TC
TS. PH
M V
N
T
80
im
1 1 2
N(x dx ,x )
+
có chuyn v tng
ng là:
1
1 1 2 1
1
u
u (x , x ) dx ;
x
∂
+∂
2
2 1 2 1
1
u
u (x , x ) dx
x
∂
+∂
.
im
1 2 2
P (x ,x dx )
+
có chuyn v
tng ng là:
1
1 1 2 2
2
u
u (x , x ) dx ;
x
∂
+∂
2
2 1 2 2
2
u
u (x , x ) dx
x
∂
+∂
.
Hình 3.4
v
dx
dx
uu+ u
x
dx
v + v
x
dx
v+ v
x
dx
u+ u
x
dx
β
α
M
P
N
PP
N
N
M


























