CƠ HC MÔI TRNG LIÊN TC TS. PHM VN T
230
Chng 6: BÀI TOÁN PH6NG TRONG H TRC TA C8C
Khi nghiên c
u tính toán cho các bài toán vành tròn,
!
a v.v… n
u dùng h
tr
c t
a
"
Descartes mô t
các

i l
$
ng (
ng su
t, bi
n d
ng) thì không thu
n ti
n b
.
ng mô t
trong
h
tr
c t
a
"
c
c. Ví d
khi nghiên c
u tr
ng thái
ng su
t, bi
n d
ng trong các
ng dày,
các
!
a quay, thanh cong, t
i nh
ng mi
n c
nh l
)
tròn c
a t
m…
Trong t
a
"
c
c, v
trí m
"
t
i
m
$
c xác

nh góc c
c θ và vect
bán kính r.
6.1 Các phng trình c bn
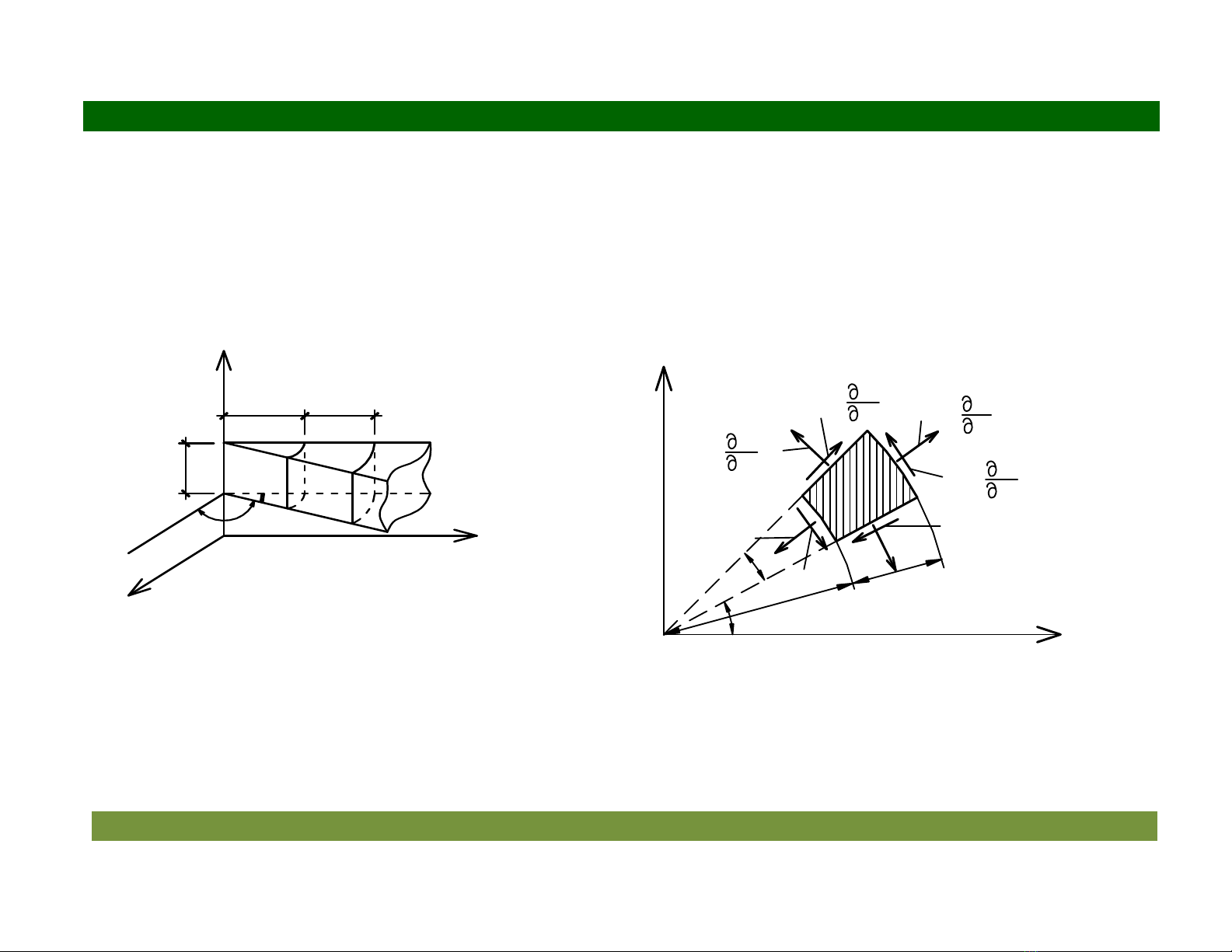
6.1.1. Các phng trình vi phân cân b-ng :
Gi
s
&
có v
t th
ch
u l
c song song v
i m
t ph
+
ng. T
i
i
m A(r,θ,z), ta c
'
t ra 1
phân t
gi
i h
n b
.
ng 6 m
t.
CƠ HC MÔI TRNG LIÊN TC TS. PHM VN T
231
$
'
"("
θ
θ
d
- 2 mt tr ng trc cách nhau m"t khong dr.
- 2 mt ph+ng cha trc z và to v i nhau m"t góc dθ.
- 2 mt ph+ng song song mt ph+ng oxy cách nhau 1 n v
Hình 6.1
y
x
o
θ
dθ
r
dr
σ
"
+ σ
"
"
d
"
τ
θ
"
+ τ
θ
"
"
d
"
σ
"
τ
θ
"
σθ
τrθ
τrθ
+
τ
"
θ
θ
dθ
σθ
+
σθ
θ
dθ
d
a
b
c
CƠ HC MÔI TRNG LIÊN TC TS. PHM VN T
232
Ký hiu:
r là trc theo hng bán kính, θ là trc i qua im ang xét A(r,θ,z) và
vuông góc v i r, ng sut trên các mt s $c ký hiu nh sau:
- Các mt nhn r làm pháp tuyn:
+ Trên mt i qua im A(r,θ,z) có các thành ph%n ng sut: σ
r
,
r
θ
τ
.
+ Trên mt i qua im A(r,θ + dθ,z), khai trin theo Taylor có các thành ph%n ng
su: r
r
d
θ
∂σ
σ + θ
,
r
r
d
θ
θ
∂τ
τ + θ
∂θ
- f
r
, f
θ
: Lc th tích hng tâm và tip tuyn tác dng lên m"t n v tip tuyn.
Xét cân b.ng ca phân t chu lc nh hình 6.1 :
r
r r
r
r r r
d d
r 0 .r.d .1 ( dr)(r dr).d .dr.1.sin ( d ).dr.1.sin
r 2 2
d d
.dr.1.cos ( d )dr.1.cos f .r.d .dr 0
2 2
θ
θ θ
θ
θ θ
∂σ
∂σ
θ θ
Σ = ⇔ − σ θ + σ + + θ− σ − σ + θ −
∂ ∂θ
∂τ
θ θ
τ + τ + θ + θ =
∂θ
CƠ HC MÔI TRNG LIÊN TC TS. PHM VN T
233
Vì bin dng bé nên
d d
sin ;
2 2
θ θ
≈
d
cos 1
2
θ
≈
Sau khi b( qua các nguyên l$ng vô cùng bé và chia cho r.dr.dθ ta $c:
r
r
r
r
1
f 0
r r r
θ
θ
σ σ
−
∂σ
∂τ
+ + + =
∂ ∂θ
(6.1)
Tng t chiu các lc lên phng θ ta $c
r r
1
2 f 0
r r r
θ θ θ
θ
∂τ ∂σ τ
+ + + =
∂ ∂θ
(6.2)
+ nh lut i ng ca ng sut tip :
r r
=
θ θ
τ τ
(6.3)
CƠ HC MÔI TRNG LIÊN TC TS. PHM VN T
234
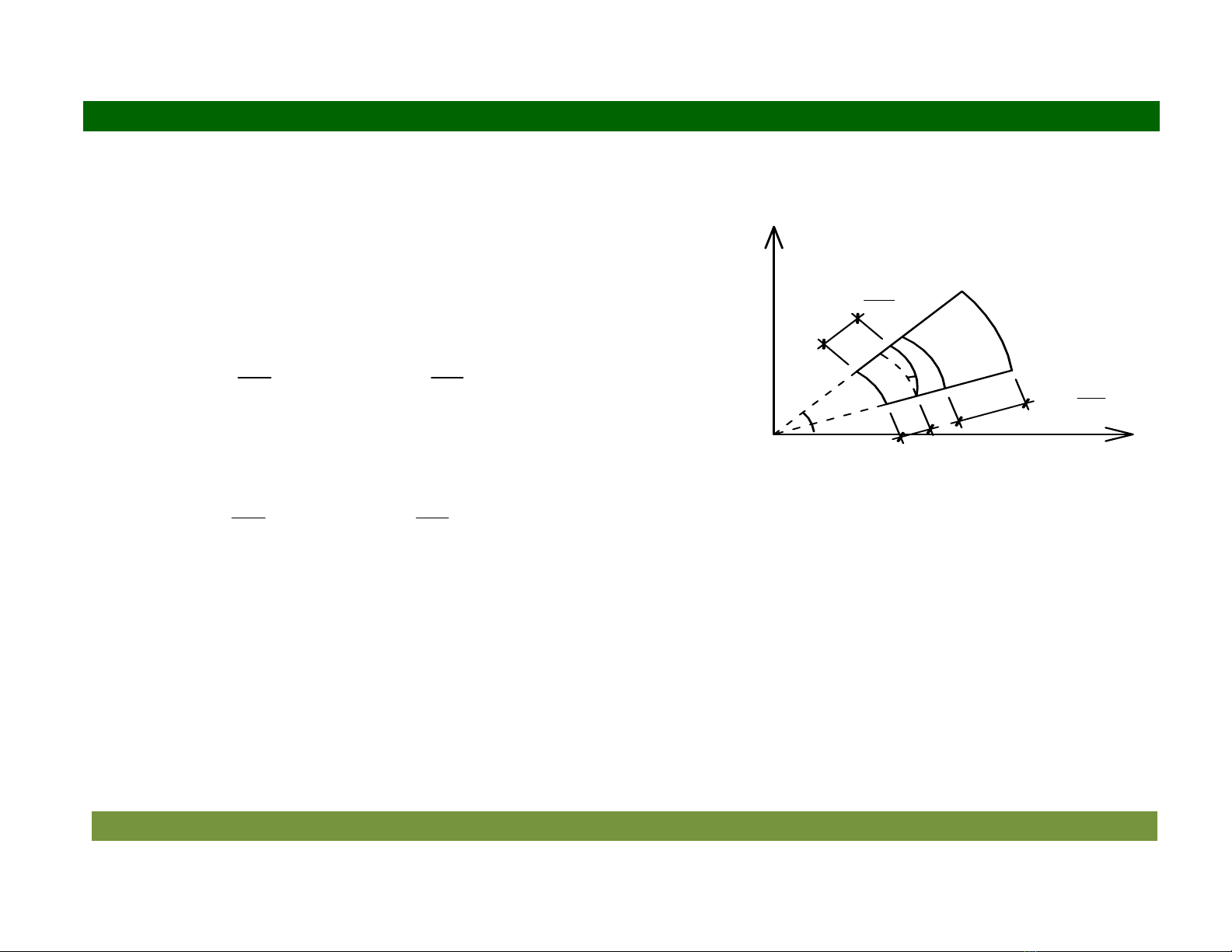
6.1.2. Các phng trình hình hc:
Chuyn v ca im A(r, 8) theo phng r, 8 là: u, v.
Chuyn v ca im B(r+dr, 8) theo 2 phng là:
u
u dr
r
∂
+∂
và
v
u dr
r
∂
+∂
Chuyn v ca im C(r, 8+d8) theo 2 phng là:
u
u d
∂
+ θ
∂θ
và
v
v dv
∂
+∂θ
Bin dng dài tng i theo phng r, 8 là: 9
r
, 9
8
Hình 6.2
* Trc tiên ch3 xét bin dng do u gây ra khi gi nguyên góc 8. Sau bin dng ABCD tr
thành A’B’C’D’ (hình 6.2):
+ Các bin dng dài tng i:
)
$
)
*
+
dr
r
u
u
∂
∂
+
θ
θ
d
u
u∂
∂
+
1
γ