CƠ HC MÔI TRNG LIÊN TC TS. PHM VN T
186
Chng 5: BÀI TOÁN PH6NG TRONG H TRC TA DESCARTES
5.1 Bài toán ph"ng
Trong ch

ng tr
c ta
ã

a ra các ph

ng trình c
b
n c
a lý thuy
t
àn h
i và các
ph

ng pháp gi
i trong tr

ng h
$
p t
ng quát. Ngh
!
a là các
6
n s
c
a bài toán ph
thu
"
c
vào 3 bi
n x, y, z (
1 2 3
x , x , x
)
ây là nh
ng bài toán không gian. Tuy nhiên trong nhi
u
tr

ng h
$
p

c bi
t bài toán d
/
n t
i các
6
n s
(bi
n d
ng ho
c
ng su
t) ch
3
ph
thu
"
c vào
2 bi
n s
(ch
+
ng h
n: x, y) nh
ng bài toán này
$
c g
i là bài toán ph
+
ng. Bài toán ph
+
ng
$
c chia thành 2 lo
i: Bài toán bi
n d
ng ph
+
ng và bài toán
ng su
t ph
+
ng. Sau
ây ta s
i nghiên c
u chi ti
t t
*
ng bài toán:
CƠ HC MÔI TRNG LIÊN TC TS. PHM VN T
187
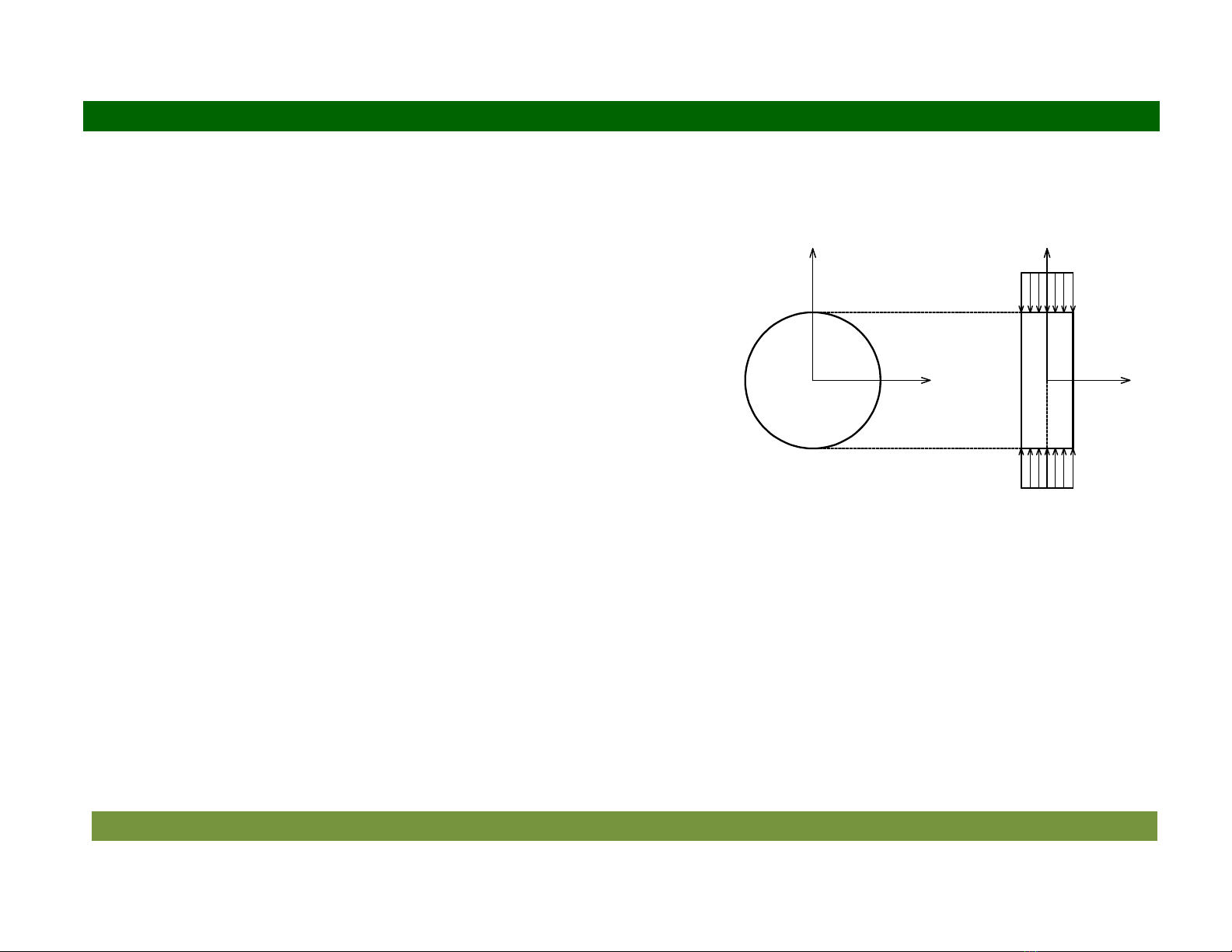
5.1 Bài toán ng sut ph"ng
Xét m
"
t t
m m
(
ng hay t
m t

ng (chi
u dày h) có
áy song song v
i m
t ph
+
ng (xoy) và ch
u t
i tr
ng
m
t s

n song song v
i
áy và phân b

u theo chi
u
dày b
n (hình 5.1).
Vì theo tr
c z không có t
i tr
ng tác d
ng t
i hai
áy nên m
i
i
m thu
"
c 2
áy b
n có:
z yz zx
0; 0; 0
σ = τ = τ =
(5.1)
Hình 5.1
Vì chi
u dày b
n khá bé nên ta có th
coi r
.
ng
ng su
t này b
.
ng không t
i m
i
i
m.
Các
ng su
t còn l
i không thay

i theo chi
u dày b
n t
c là không ph
thu
"
c vào t
a
"
z. Chúng là hàm c
a t
a
"
x, y và
$
c bi
u di
-
n nh
sau:
y
xz
q
q
y
CƠ HC MÔI TRNG LIÊN TC TS. PHM VN T
188
x 1
y 2
xy 3
F (x, y);
F (x, y);
σ =
σ =
τ =
(5.2)
Nh
v
y, trong bài toán này các nghi
m
ng su
t c
a bài toán n
.
m trong m
"
t m
t
ph
+
ng và bài toán này
$
c g
i là bài toán
ng su
t ph
+
ng.

nh lu
t Hooke bi
u di
-
n bi
n d
ng qua
ng su
t:
( )
( )
( )
x y
x x y z
y x
y y z x
x y
z z x y
xy
xy
( )
1( )
E E
( )
1( )
E E
( )
1( )
E E
2(1 )
E
σ − υσ
ε = σ − υ σ + σ =
σ − υσ
ε = σ − υ σ + σ =
−υ σ + σ
ε = σ − υ σ + σ =
+ υ τ
γ =
(5.3)
CƠ HC MÔI TRNG LIÊN TC TS. PHM VN T
189

nh lu
t Hooke bi
u di
-
n
ng su
t qua bi
n d
ng:
x x
y y
x xy
2
2
σ = λθ + µε
σ = λθ + µε
τ = µγ
(5.4)
trong
ó:
x y z
θ = ε + ε + ε
5.3 Bài toán bin dng ph"ng
Gi
s
&
m
i
i
m trong v
t th
àn h
i ta có chuy
n v
ch
3
ph
thu
"
c vào 2 trong 3 bi
n
x, y, z (ch
+
ng h
n x, y) ngh
!
a là:
1
2
u f (x, y)
v f (x, y)
w 0
=
=
=
(5.5)
CƠ HC MÔI TRNG LIÊN TC TS. PHM VN T
190
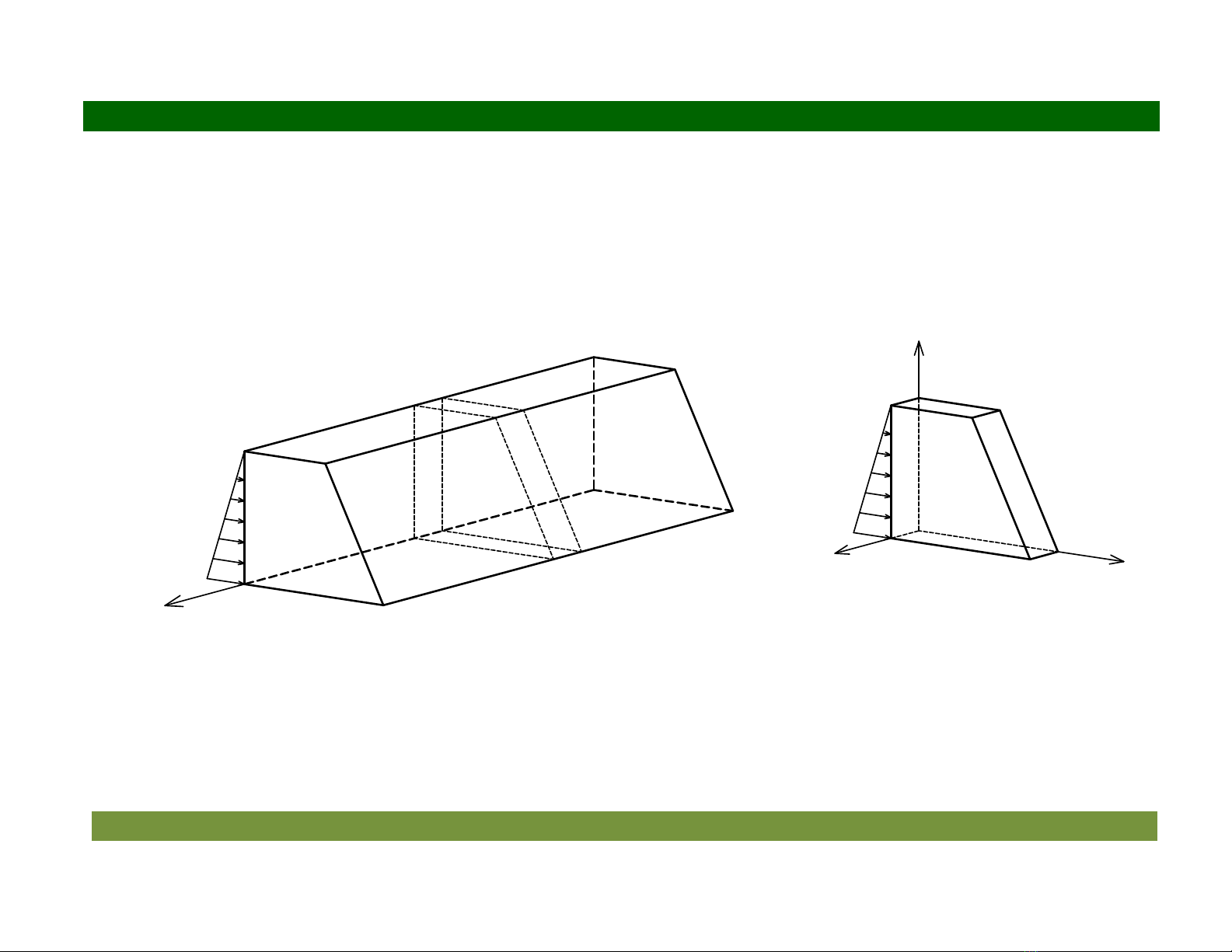
Ví d
: Xét t

ng ch
'
n dài ch
u áp l
c c
a n
c nh
hình 5.2a. Ta xét trong m
"
t

n v
dài t

ng ch
'
n thì coi nh
t
m b
k
7
p gi
a chi
u dài v
t nên không có bi
n d
ng dài theo
ph

ng theo ph

ng b
dài (ph

ng z) (hình 5.2b)
Hình 5.2
Khi
ó các thành ph
%
n bi
n d
ng t
i m
"
t
i
m b
t k
#
trong t
m:
zzx
y
a) b)