Chương 5: Các quy luật điều chỉnh tuyến tính cơ bản
Tỷ lệ: P (Propotional)
Tích phân: I (Integral)
Tỷ lệ - Tích phân: PI
Tỷ lệ - Vi phân: PD
Tỷ lệ - Tích phân - Vi phân: PID
100
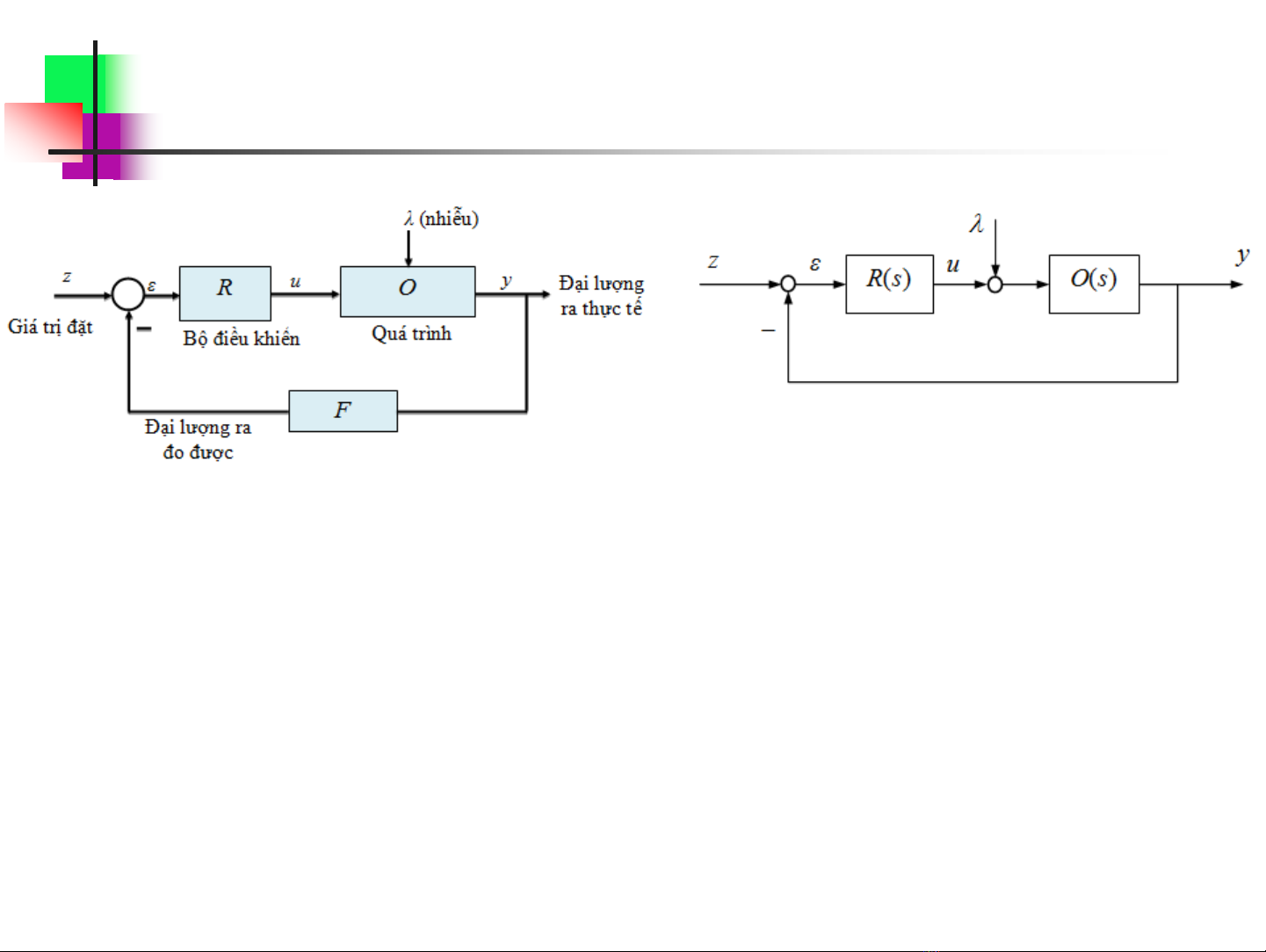
Hệ thống điều chỉnh điển hình
Quan hệ vào ra:
Kp – hệ số truyền, u(t) – tác động điều chỉnh; ε(t) – sai lệch điều
chỉnh
Hàm truyền:
Đáp ứng quá độ:
→ bộ điều chỉnh P (bộ điều chỉnh tĩnh), bộ điều chỉnh
tác động nhanh
101
Chương 5: Các quy luật điều chỉnh tuyến tính cơ bản
Quy luật tỷ lệ
p
K
s
su
sR )(
)(
)(
( ) ( ) p
u t K t
0
() p
u t K
Quan hệ vào ra:
Kp - hệ số truyền; Ti - hằng số tích phân; c0 = KP/Ti
Hàm truyền:
Đáp ứng quá độ:
→ bộ điều chỉnh I (bộ điều chỉnh phi tĩnh), bộ điều
chỉnh chậm
Chương 5: Các quy luật điều chỉnh tuyến tính cơ bản
Quy luật tích phân
102
dcd
T
K
tu
tt
i
p
0
0
0
)()()(
s
c
sT
K
sR
i
p0
)(
00
, 0()u t c t t

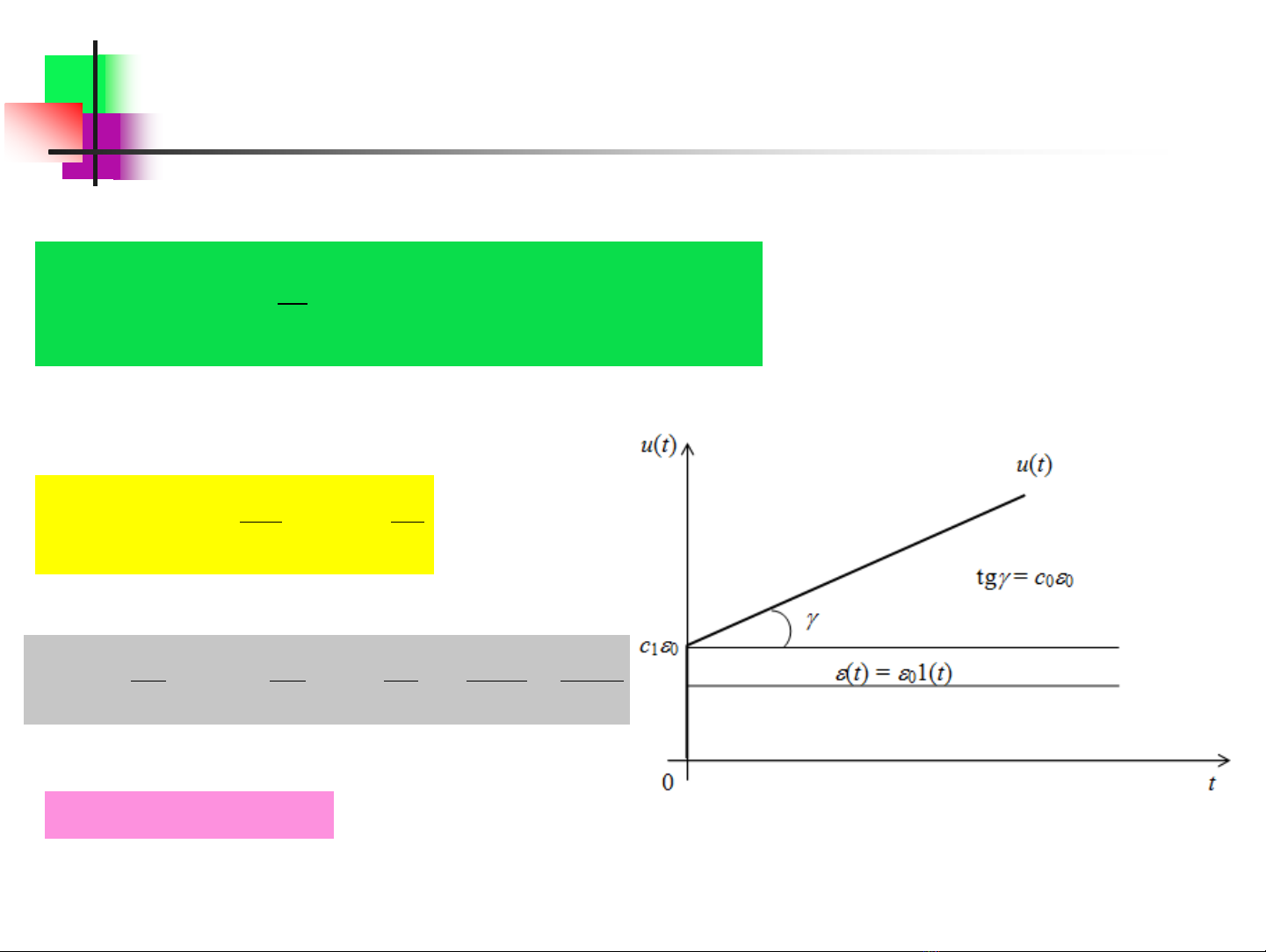
Quan hệ vào ra:
Kp – hệ số truyền; Ti - hằng số tích phân; c0=Kp/Ti, c1=Kp
Hàm truyền:
Ảnh đáp ứng ra:
Đáp ứng ra:
Chương 5: Các quy luật điều chỉnh tuyến tính cơ bản
Quy luật tỷ lệ - tích phân
103
dctcd
T
tKtu
tt
i
p
0
01
0
)()()(
1
)()(
s
c
c
sT
KsR
i
p0
1
)
1
1()(
Đặc tính quá độ của bộ điều chỉnh PI
→ Bộ điều chỉnh PI có tính chất tác động nhanh nhờ thành phần tỷ lệ (P) và có tính chất phi tĩnh
nhờ thành phần tích phân (I)
1 0 0 0
()u t c c t


104
Chương 5: Các quy luật điều chỉnh tuyến tính cơ bản
Quy luật tỷ lệ - vi phân
Quan hệ vào ra:
Hàm truyền:
Ảnh đáp ứng ra:
Đáp ứng ra:
u(t) = c10 + c20(t)
dt
td
ctc
dt
td
TtKtu dp
)(
)(
)(
)()( 21
sccsTKsR dp .)1( 21
02
01
21
0)()(
c
s
c
scc
s
sU
10
, khi 0,
() , khi 0.
t
ut ct


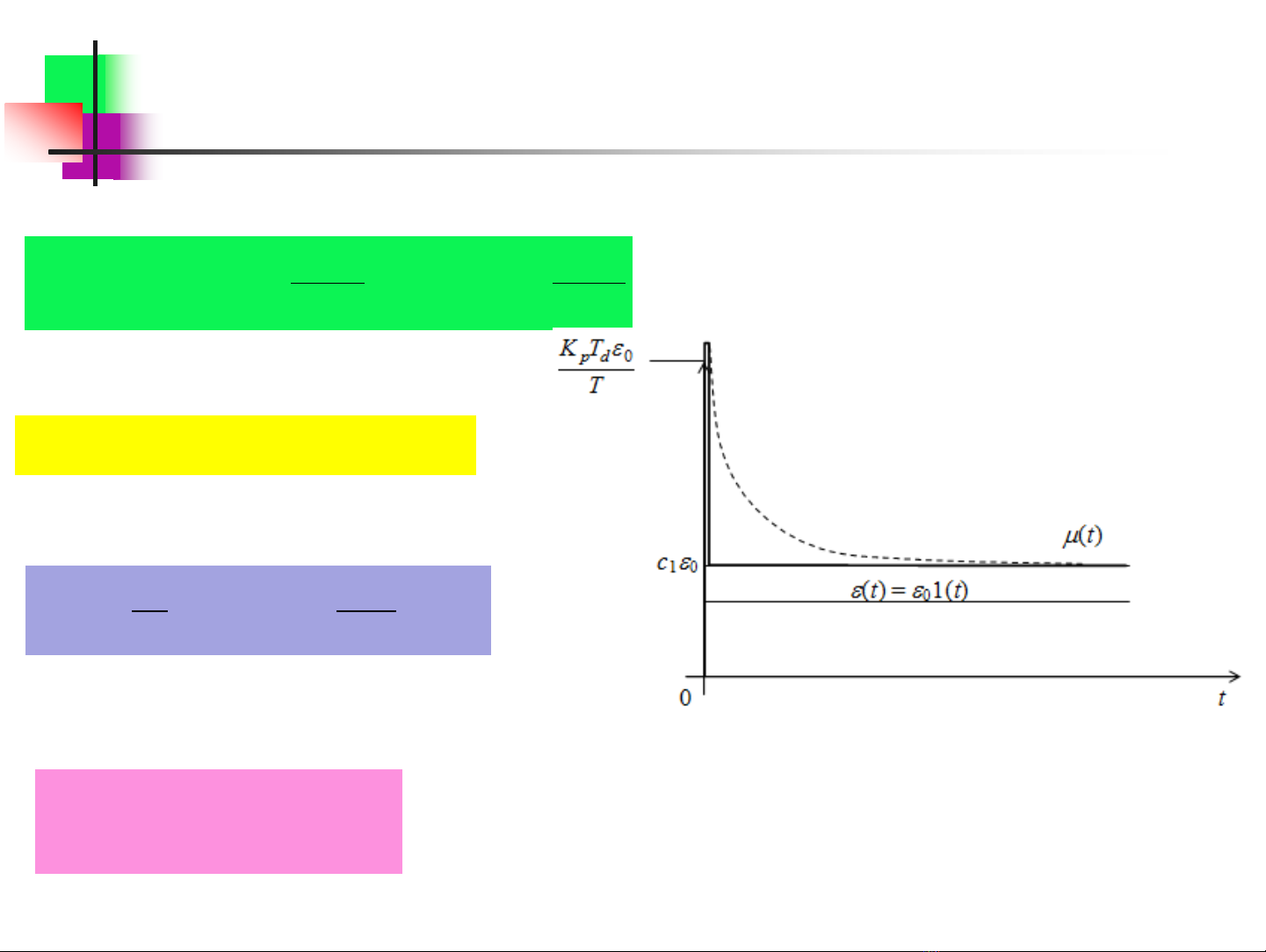
Đặc tính quá độ của bộ điều chỉnh PD
→ với bộ đc PD, thành phần P quy định tính chất tác động nhanh,
thành phần D dự báo xu thế thay đổi của đại lượng điều chỉnh và
nhờ đó tạo khả năng ngăn chặn sai số điều chỉnh đồng thời tăng độ
ổn định của hệ thống, là bộ điều chỉnh tĩnh học
c1=Kp – hệ số truyền; Td – hằng số vi phân;
c2=KpTd – hệ số vi phân