Chế độ xác lập là trạng thái của hệ thống xảy ra theo
một quy luật cố định phụ thuộc vào tín hiệu đầu vào
Quá trình quá độ xảy ra khi hệ thống chuyển từ chế
độ xác lập này sang chế độ xác lập khác
128
Chương 6: Tính chất ổn định của hệ thống điều khiển
Khái niệm về sự ổn định của hệ thống
Ổn định là khả năng của một hệ động học chuyển từ trạng
thái chuyển động có kích động trở về trạng thái cân bằng ban
đầu sau khi triệt tiêu các tín hiệu kích động
129
Chương 6: Tính chất ổn định của hệ thống điều khiển
Khái niệm về sự ổn định của hệ thống
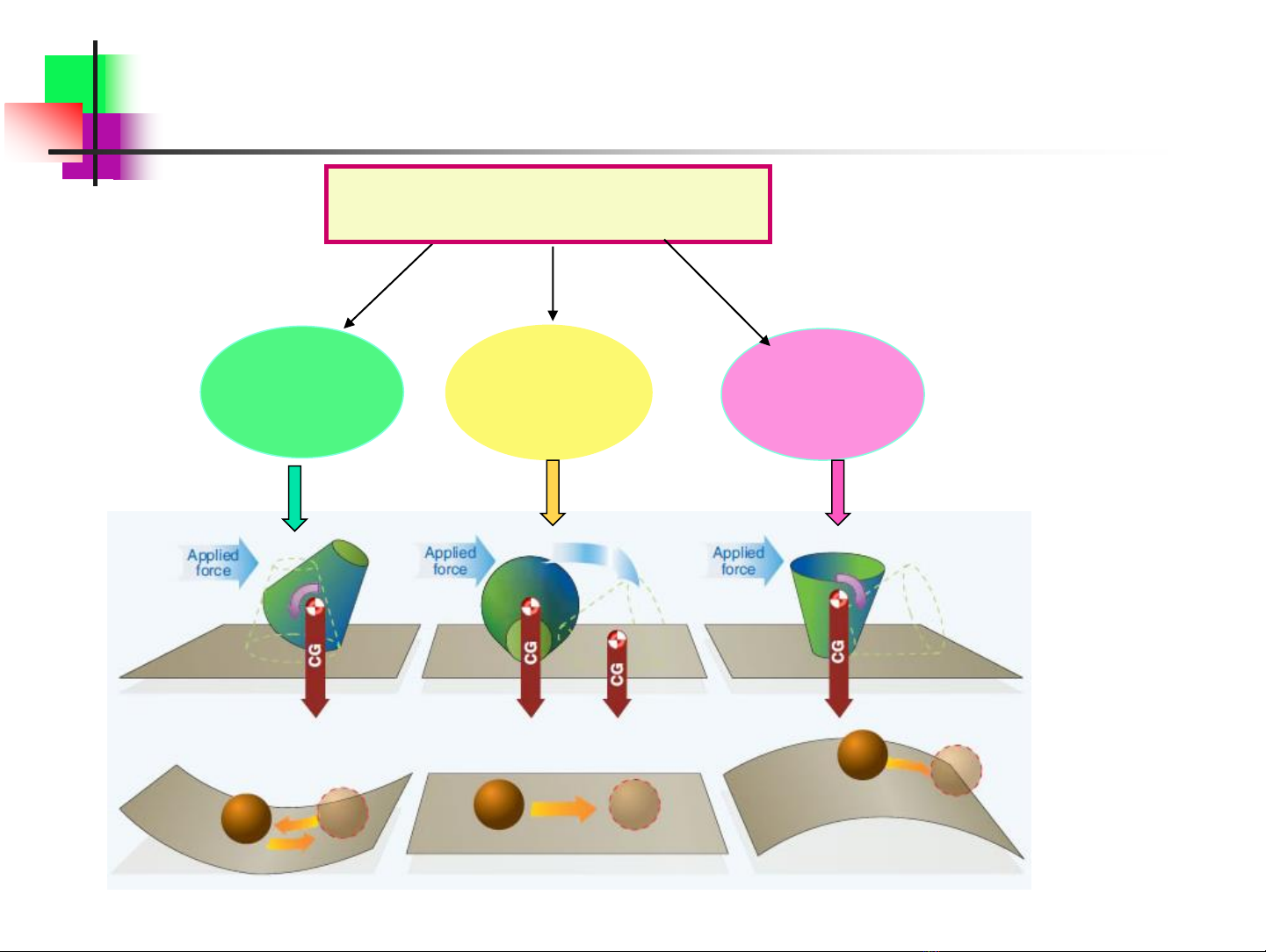
Hình ảnh tương tự về sự ổn định của một hệ động học
Hệ ổn định
Hệ trung
tính
Hệ động học
Hệ không
ổn định
130
Chương 6: Tính chất ổn định của hệ thống điều khiển
Điều kiện ổn định của hệ tuyến tính
gbgbgbyayaya m
mm
n
nn ...... )1(
1
)(
0
)1(
1
)(
0
Phương trình vi phân mô tả một hệ điều khiển tuyến tính có dạng chung
Nghiệm tổng quát của phương trình:
Triệt bỏ tín hiệu kích thích: g(t)=0, thì thành phần chuyển động cưỡng bức
cũng triệt tiêu: yr(t)=0. Hệ ổn định khi:
0
r
y t y t y t
0)(lim 0
ty
t
y0(t) – nghiệm TQ của phương trình vi phân thuần nhất, đặc trưng cho thành phần
chuyển động tự do của đáp ứng ra thể hiện ở quá trình quá độ, do bản chất động học
của hệ thống quyết định
yr(t) – nghiệm riêng, đặc trưng cho thành phần chuyển động xác lập của đáp ứng ra,
xảy ra và phụ thuộc vào tác động kích thích g(t)
131
Chương 6: Tính chất ổn định của hệ thống điều khiển
Điều kiện ổn định của hệ tuyến tính (tiếp)
Định nghĩa về sự ổn định tiệm cận của Liapunov (phương trình đặc tính):
Trên miền ảnh Laplace:
Nghiệm của phương trình:
0)(...
)()(
0
1
0
1
1
0
0
tya
dt
tyd
a
dt
tyd
an
n
n
n
n
1
01 ... 0
nn n
a s a s a
n
i
ts
ii
ecty
1
0)(
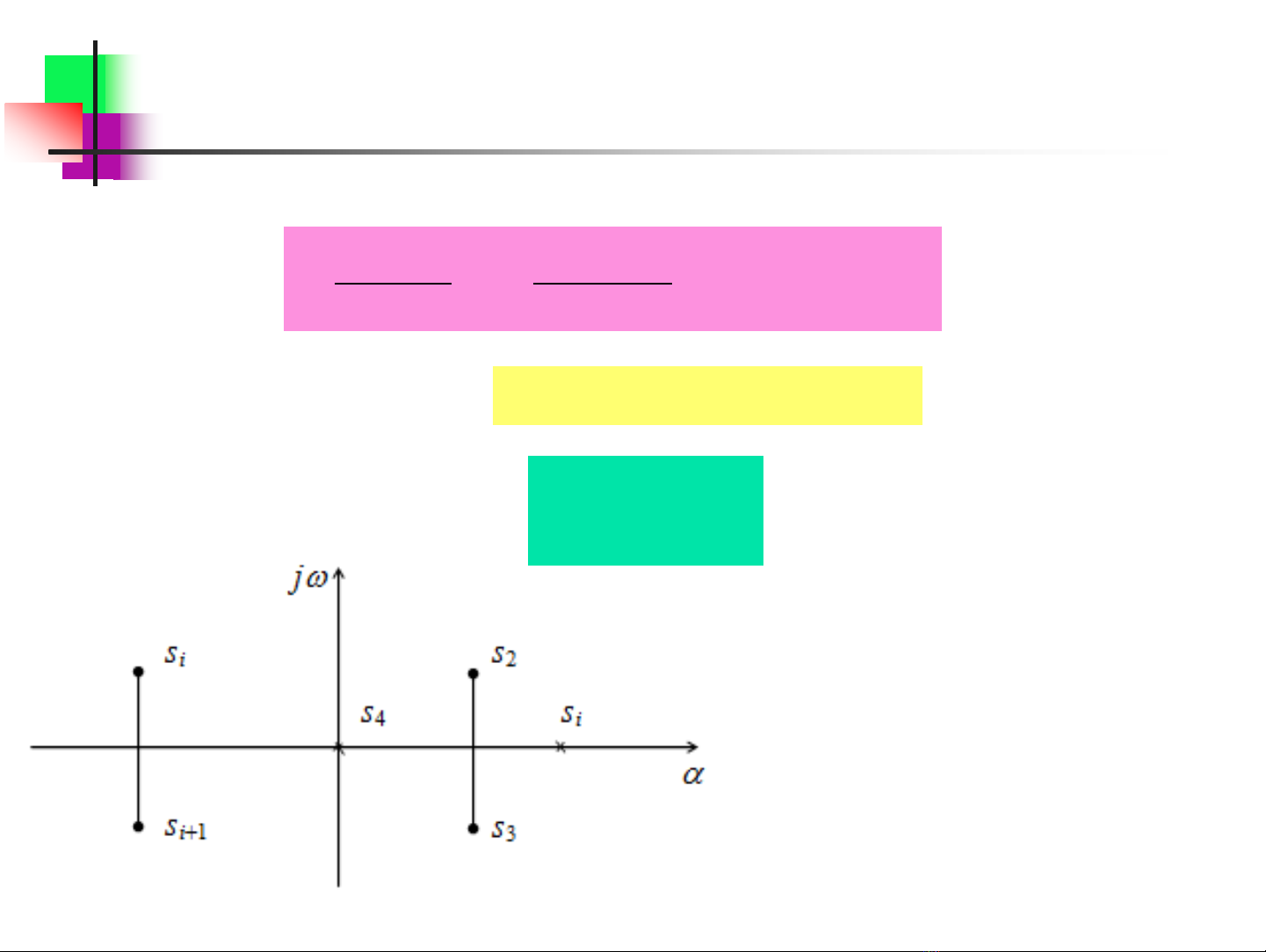
ci là số thực nếu si là nghiệm
thực, và ci là hằng số phức nếu
si là nghiệm phức
Sự phân bố các nghiệm phương trình đặc tính trên mặt phẳng phức
Chương 6: Tính chất ổn định của hệ thống điều khiển
Điều kiện ổn định của hệ tuyến tính (tiếp)
Xét riêng thành phần chuyển động tương ứng với nghiệm thực
I
ci là số thực.
Xét cáctrường hợp đối với
i:
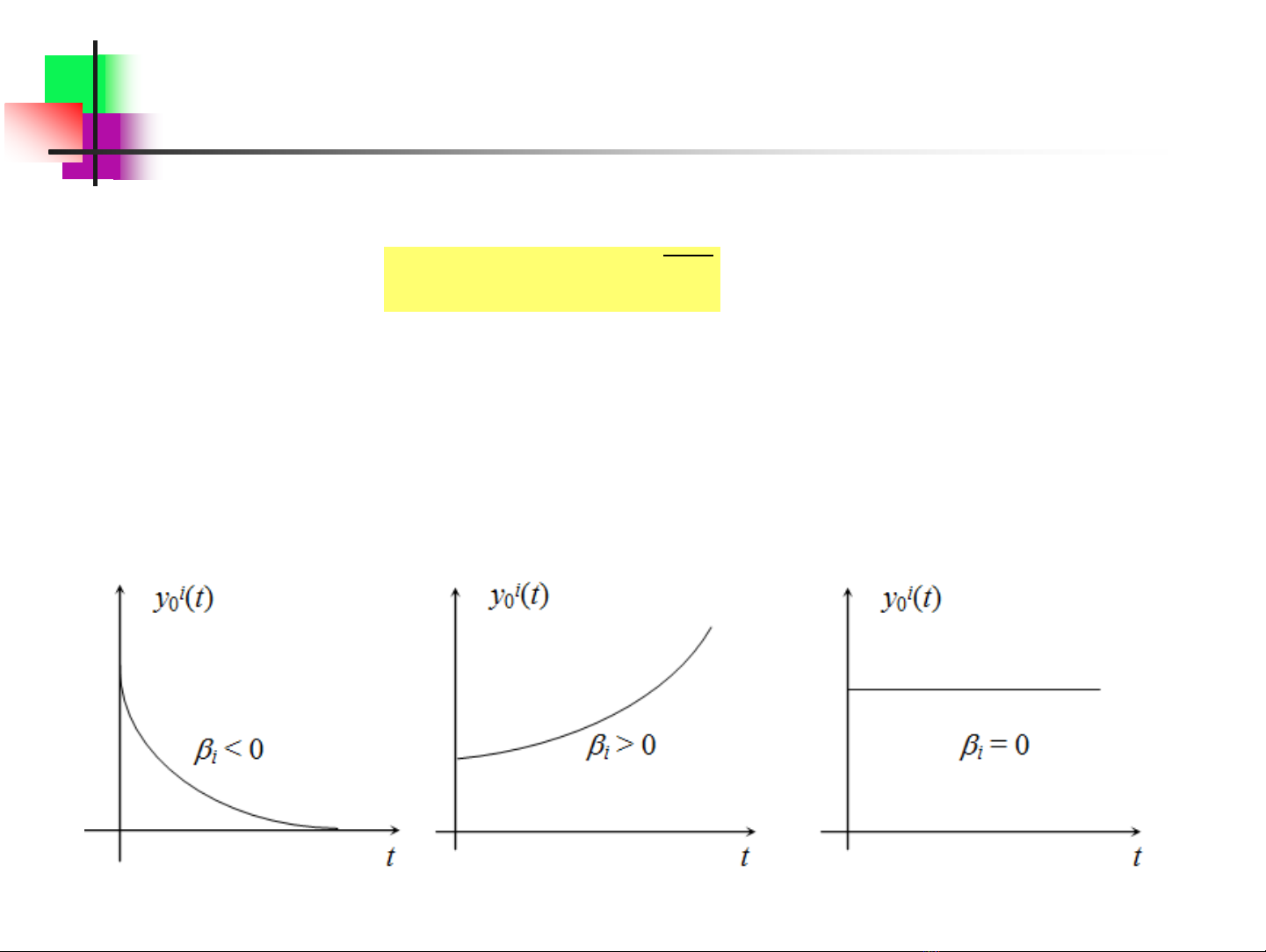
nếu
i < 0 thì y0i(t) là hàm đơn điệu giảm đến 0
nếu
i > 0 thì y0i(t) là hàm đơn điệu tăng đến
nếu
i =0 thì y0i(t) = ci là hằng số cố định
132
piecty t
i
ii,1,)(
0
Các thành phần chuyển động tự do của hệ thống, ứng với các nghiệm thực khác nhau