Phụtrách: TS. Đinh Bá Hùng Anh
Tel: 01647.077.055/090.9192.766
Mail: anhdbh_ise7@yahoo.com
Phân tích Định lượng
Lý thuyết ra quyết định
Có sáu bước cơ bản trong quá trình ra quyết định
Bước 1: Xác định vấn đề.
Bước 2: Tìm các phương án có thể để đưa ra các quyết định tương ứng.
Bước 3: Xác định các kết quả có thể xảy ra theo các tình huống khác nhau.
Bước 4: Xác định chi phí hay lợi ích thu được ứng với tổ hợp từng tình huống
kết quả và từng phương án.
Bước 5: Xác định môi trường và lựa chọn một mô hình ra quyết định phù hợp.
Bước 6: Sử dụng mô hình và ra quyết định.
Chương 1: Lý thuyết ra quyết định
Nhà đầu tư xem xét đầu tư 10 tỷ đồng
(a) Thị trường chứng khoán
(b) Gửi ngân hàng với lãi suất cố định 9%/năm.
Kết quả đầu tư chứng khoán:
(1) Thị trường chứng khoán lạc quan (optimistic): lợi tức 14%/năm
(2) Bình thường (moderate) lợi tức 9% (= gửi ngân hàng)
(3) Bi quan (Pessimistic) lợi tức = 0 (bảo toàn vốn)
Cho xác suất để thị trường có viễn cảnh lạc quan (0,3), bình thường (0,5)
và bi quan (0,2).
Hãy ra quyết định đầu tư?
Bài toán 1:
Lý thuyết ra quyết định
Bước 1. Vấn đề: quyết định đầu tư hay không. Nếu có thì đầu tư vào chứng
khoán hay ngân hàng?
Bước 2. Các phương án có thể chọn lựa là:
•Phương án 1: Gửi toàn bộ số tiền vào ngân hàng
•Phương án 2: Đầu tư chứng khoán
•Phương án 3. Không đầu tư.
Bước 3. Các tình huống kết quả có thể xảy ra:
-Thị trường lạc quan
-Thị trường bình thường
-Thị trường bi quan
Bước 4. Xác định lợi ích - chi phí của từng phương án
Lợi tức theo phương án được biểu diễn qua bảng ra quyết định (Decision Table)
Lý thuyết ra quyết định
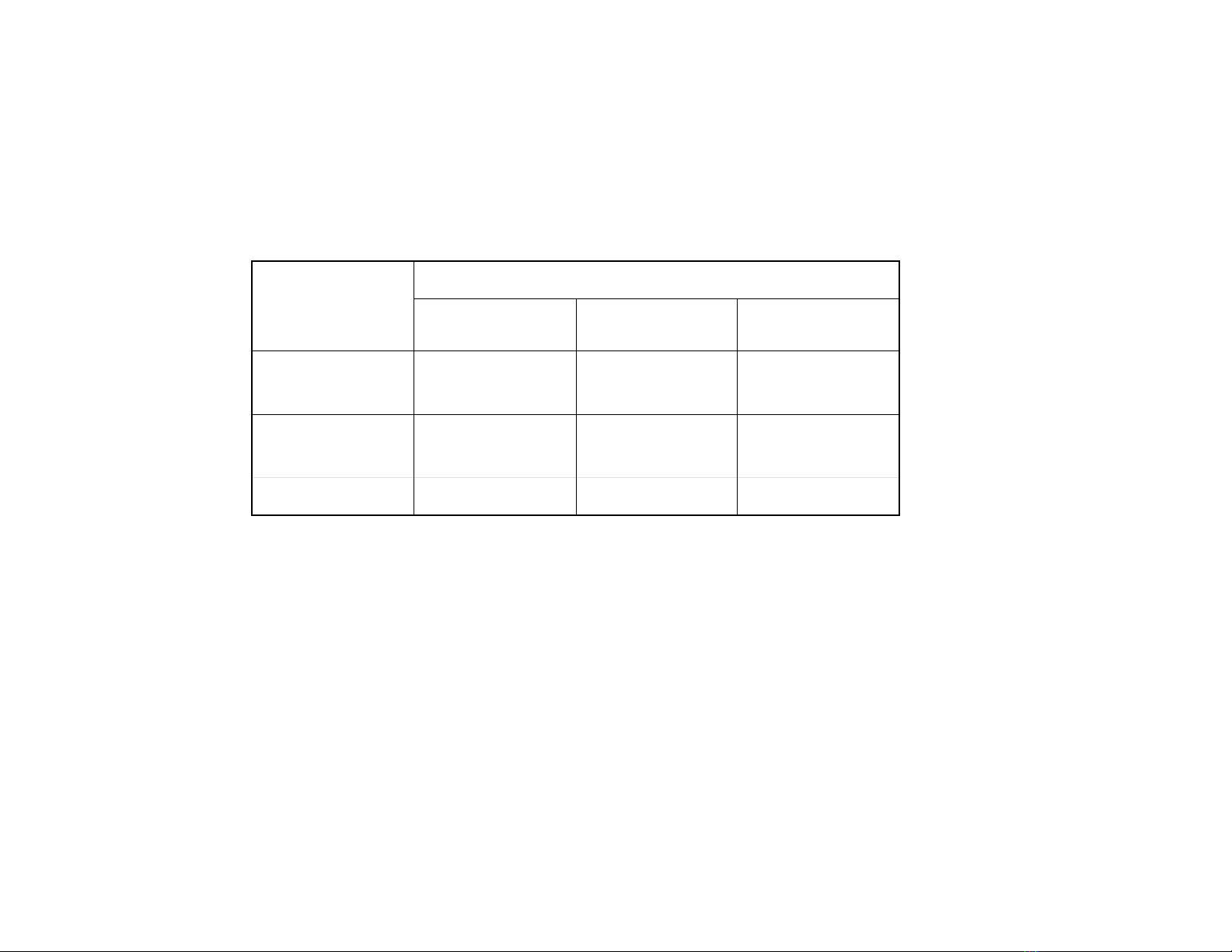
Bảng 1. Bảng ra quyết định
Đvt: tỷ VND
Các phương
án
Các trạng thái tự nhiên (state of nation)
Lạc quan Bình thường Bi quan
Gửi ngân
hàng
0,9 0,9 0,9
Mua chứng
khoán
1,4 0,9 0
Không đầutư000
Bước 5. Xác định môi trường ra quyết định: Xác định, rủi ro, không xác định
Bước 6. Lựa chọn mô hình và ra quyết định.
Lý thuyết ra quyết định