TRƯỜNG ĐẠI HỌC TÀI CHÍNH – MARKETING
BỘ MÔN TOÁN – THỐNG KÊ
Slide bài giảng
KINH TẾ LƯỢNG
THÀNH PHỐ HỒ CHÍ MINH - 2022
9/7/2022
1
Chương 0
Ôn Tập
2
1. Đạo hàm (tỷ lệ sự thay đổi)
2) Đạo hàm tại điểm
3) Đạo hàm riêng
4) Điều kiện cần của cực trị
5) Điều kiện đủ của cực trị
6) Phân phối xác suất
Nội dung
9/7/2022
2
1. Đạo hàm (tỷ lệ sự thay đổi)
Xét hàm số Y=f(X). Trong đó
Y : Biến phụ thuộc, biến được giải
thích, biến nội sinh, biến hồi quy.
X : Biến độc lập, biến giải thích,
biến ngoại sinh.
Ví dụ 1: Thu nhập (X) – Chi tiêu (Y).
Lạm phát (X) – Lãi suất (Y).
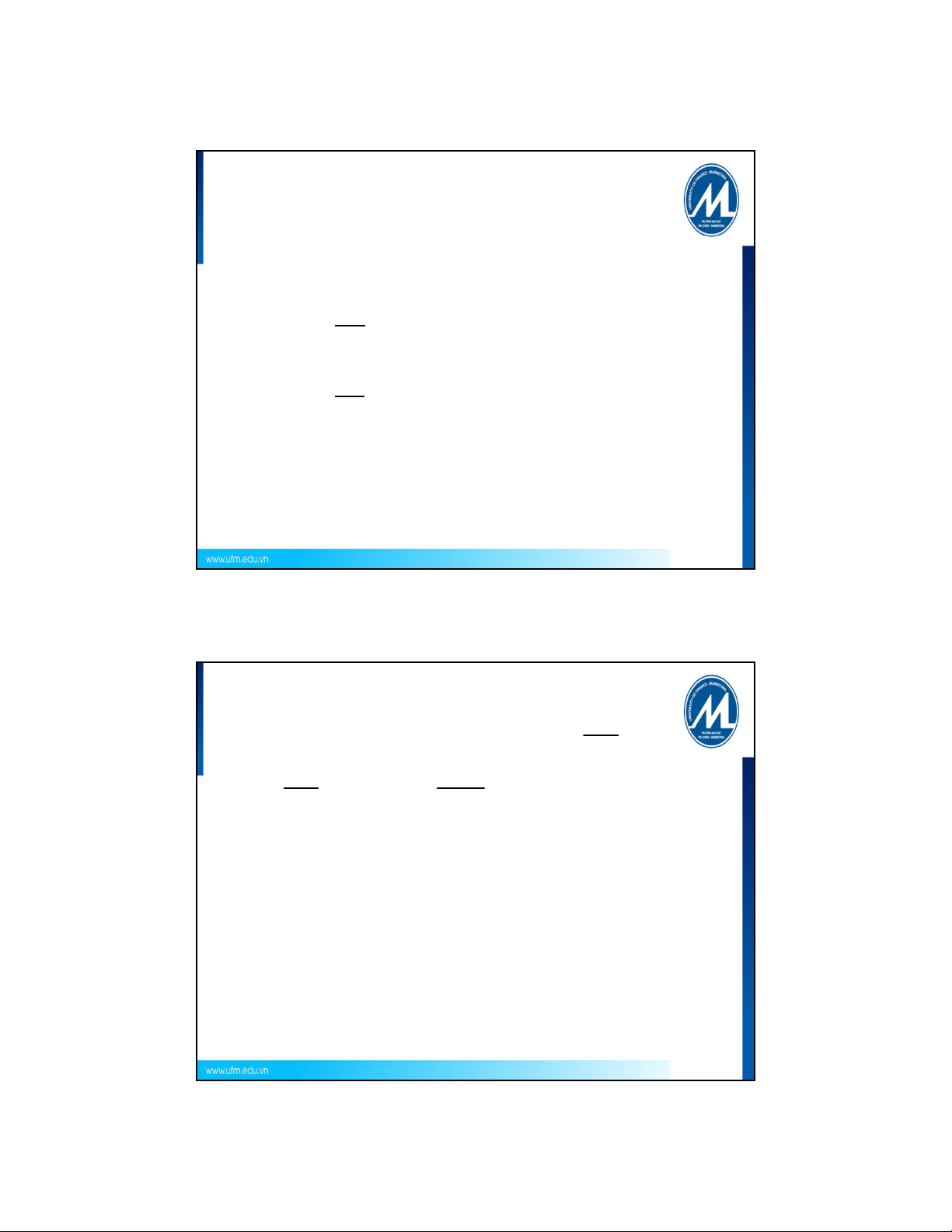
2. Đạo hàm tại điểm. Xét hàm số:
Sự thay đổi của y theo x:
Tỷ lệ sự thay đổi của y theo x xung quanh
điểm a.
Ví dụ 2: Xét mối quan hệ:
Giả sử: x: lạm phát, y: lãi suất và
Ý nghĩa: Nếu LP tăng 1% thì LS tăng 1.25%.
f (x) f (a) y
x a x
y f (x)
/ /
y f (a) y / x
x
y f (x)
/
f (5) 1.25
: sự thay đổi của y
y
: sự thay đổi của x
9/7/2022
3
3. Đạo hàm riêng. Xét hàm số:
z : là biến phụ thuộc (biến được giải thích)
x,y : là biến độc lập (biến giải thích)
3.1. Đạo hàm riêng của z theo x
3.2. Đạo hàm riêng của z theo y
z z
(3,2) 0.4; (3,2) 0.1
x y
x 0
z f (x x,y) f (x, y)
lim ; ( x, y 0)
x x
y 0
z f (x, y y) f (x,y)
lim ; ( x 0, y)
y y
Ví dụ 3:
6
Ví dụ 4: Tính đạo hàm riêng của hàm số:
3 3
2 2
1. f (x,y) x y 6xy 2x 3y 1
2. f (x,y) ln(x y )
2 2
2 2 2 2
f f
1. (x,y) 3x 6y 2; (x,y) 3y 6x 3
x y
f 2x f 2y
2. (x,y) ; (x,y)
x x y y x y
Giải
9/7/2022
4
4. Điều kiện cần của cực trị.
Xét hàm số:
Hàm số đạt cực trị tại
0 0
(x ,y )
0 0
0 0
f(x ,y ) 0
x
(*)
f(x ,y ) 0
y
Nếu thỏa (*) thì được gọi
là điểm dừng.
0 0
(x ,y )
0 0
(x ,y )
Th1: Nếu và thì là cực tiểu.
5. Điều kiện đủ của cực trị.
Xét điểm dừng: . Đặt
2
0 0
2
f
A (x , y ),
x
0 0
(x ,y )
0
A 0
2 2
2
0 0 0 0
2
f f
C (x ,y ), B (x ,y ), AC B
y x y
0 0
(x , y )
Th2: Nếu và thì là cực đại.
Th3: Nếu thì không là cực trị.
Th4: Nếu chưa đủ cơ sở kết luận.
0
0
0
A 0
0 0
(x ,y )
0 0
(x , y )