

(Ordinary Least Square)
Gi s có m t m u g m n ả ử ộ ẫ ồ
Gi s có m t m u g m n ả ử ộ ẫ ồ
quan sát (Y
quan sát (Yi
i, X
, Xi
i), (i = 1, 2, . . . ,
), (i = 1, 2, . . . ,
n)
n)
Theo pp OLS, ta ph i tìm ả
Theo pp OLS, ta ph i tìm ả
sao cho nó càng g n v i giá tr ầ ớ ị
sao cho nó càng g n v i giá tr ầ ớ ị
th c (Yự
th c (Yựi
i) càng t t, t c ph n ố ứ ầ
) càng t t, t c ph n ố ứ ầ
d
dư
ư:
:
i
Y
ˆ

e
ei
i = Y
= Yi
i
=
= Y
Yi
i
X
Xi
i
i
Y
ˆ
càng nh càng t tỏ ố
càng nh càng t tỏ ố
1
ˆ
2
ˆ
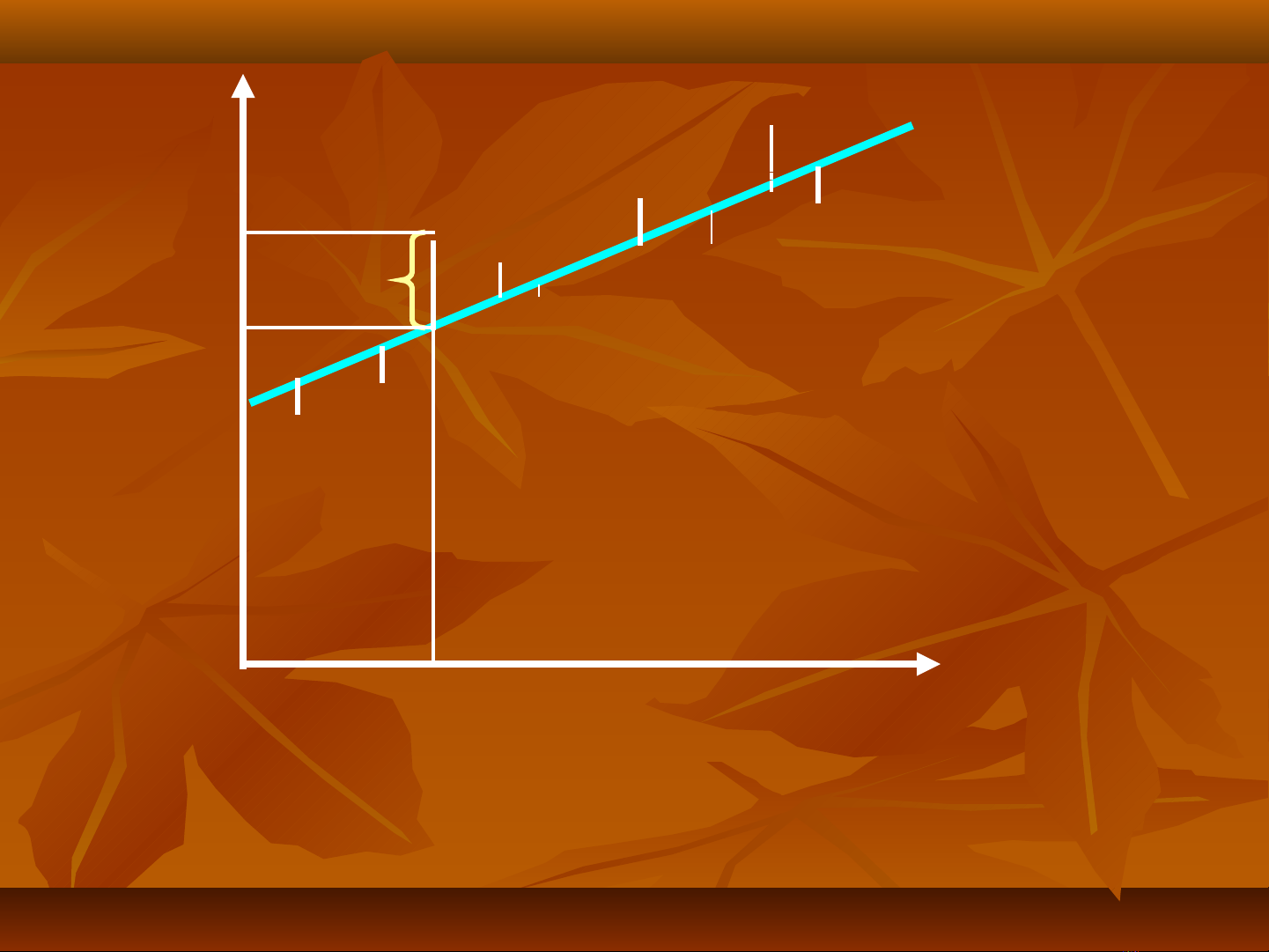
Y
Y
.
.
..
.
.
..
.
.
.
e
ei
i
X
X
X
Xi
i
Y
Yi
i
Y
Y^
^
i
i
.
..
.
.
0
0
SRF
SRF

Do e
Do ei
i có th dể
có th dểươ
ương, có
ng, có
th âm, nên ta c n tìm ể ầ
th âm, nên ta c n tìm ể ầ
SRF sao cho t ng bình ổ
SRF sao cho t ng bình ổ
ph
phươ
ương c a các ph n dủ ầ
ng c a các ph n dủ ầ ư
ư
đ
đt c c ti u.ạ ự ể
t c c ti u.ạ ự ể
T c , ph i tho ứ ả ả
T c , ph i tho ứ ả ả
mãn
mãn đ
đi u ki n: ề ệ
i u ki n: ề ệ
1
ˆ
2
ˆ











![240 câu hỏi trắc nghiệm Kinh tế vĩ mô [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2026/20260126/hoaphuong0906/135x160/51471769415801.jpg)

![Câu hỏi ôn tập Kinh tế môi trường: Tổng hợp [mới nhất/chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251223/hoaphuong0906/135x160/56451769158974.jpg)




![Giáo trình Kinh tế quản lý [Chuẩn Nhất/Tốt Nhất/Chi Tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2026/20260122/lionelmessi01/135x160/91721769078167.jpg)







