Lý thuyếtĐiềukhiểntựđộng 1
Ziegler-Nichols
Tốiưuđộ lớn
Tốiưuđốixứng
ThS. Đỗ Tú Anh
Bộmôn Điềukhiểntựđộng
Khoa Điện, Trường ĐHBK HN
cuu duong than cong . com
12-1
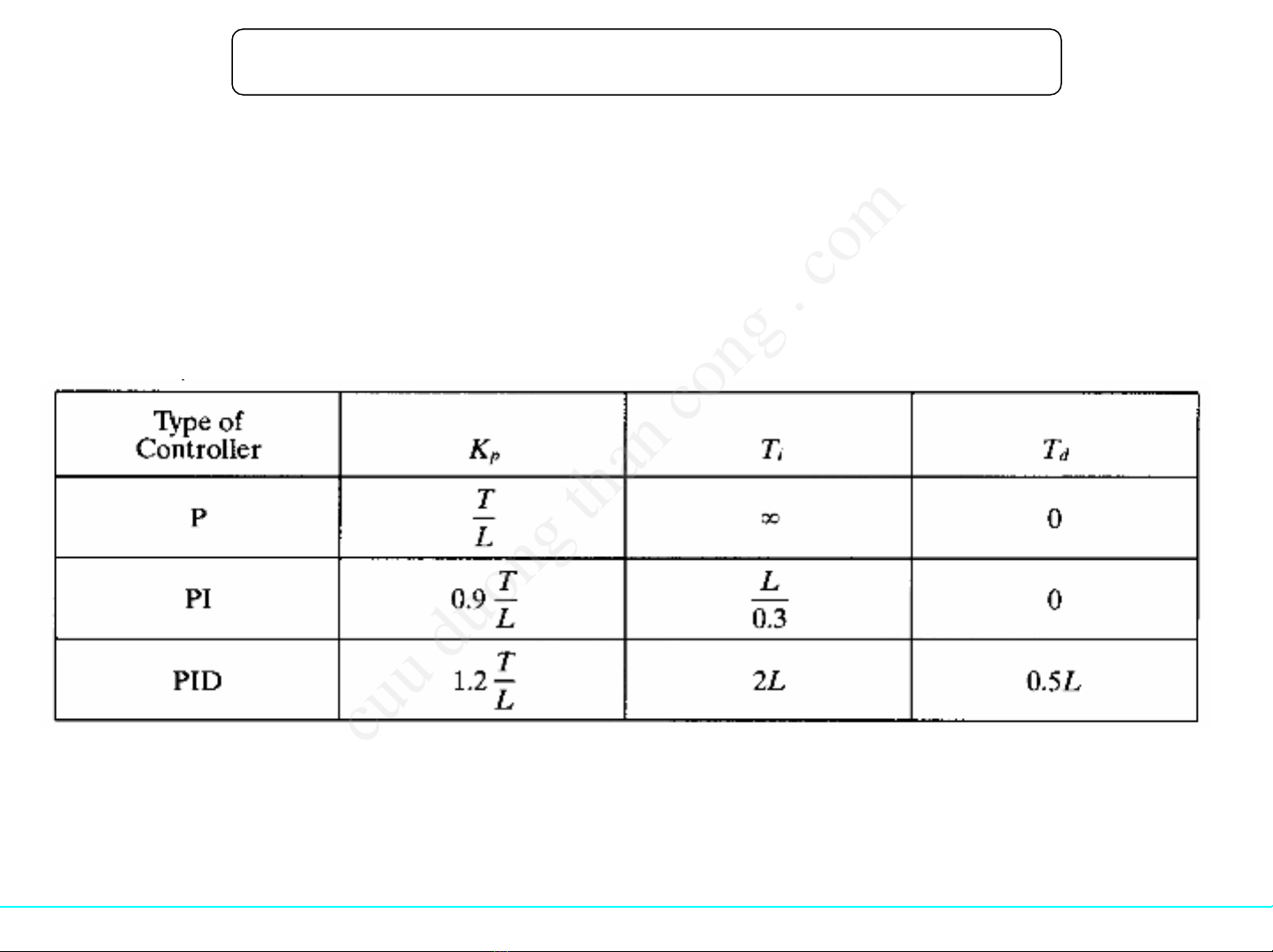
Phương pháp Ziegler-Nichols
Đặcđiểmcủaphương pháp
•Làphương pháp thựcnghiệmđể xác định các tham sốcủabộđkPID
•Rấtthuậntiện khi mô hình toán họccủađốitượng chưabiếttrước
•Đáp ứng nhậnđượccóđộ quá điềuchỉnh khoảng 25%
Phương pháp Ziegler-Nichols 1
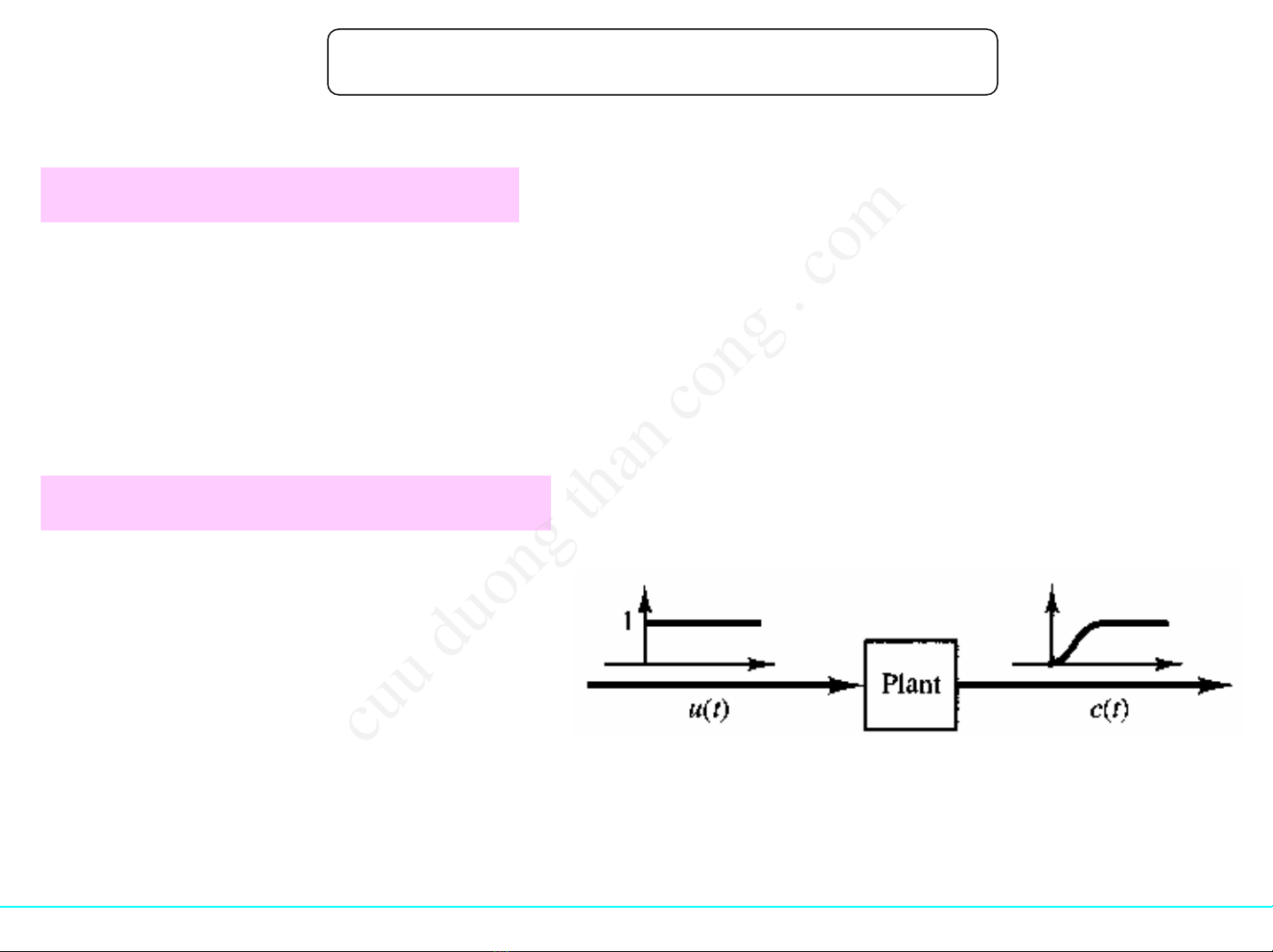
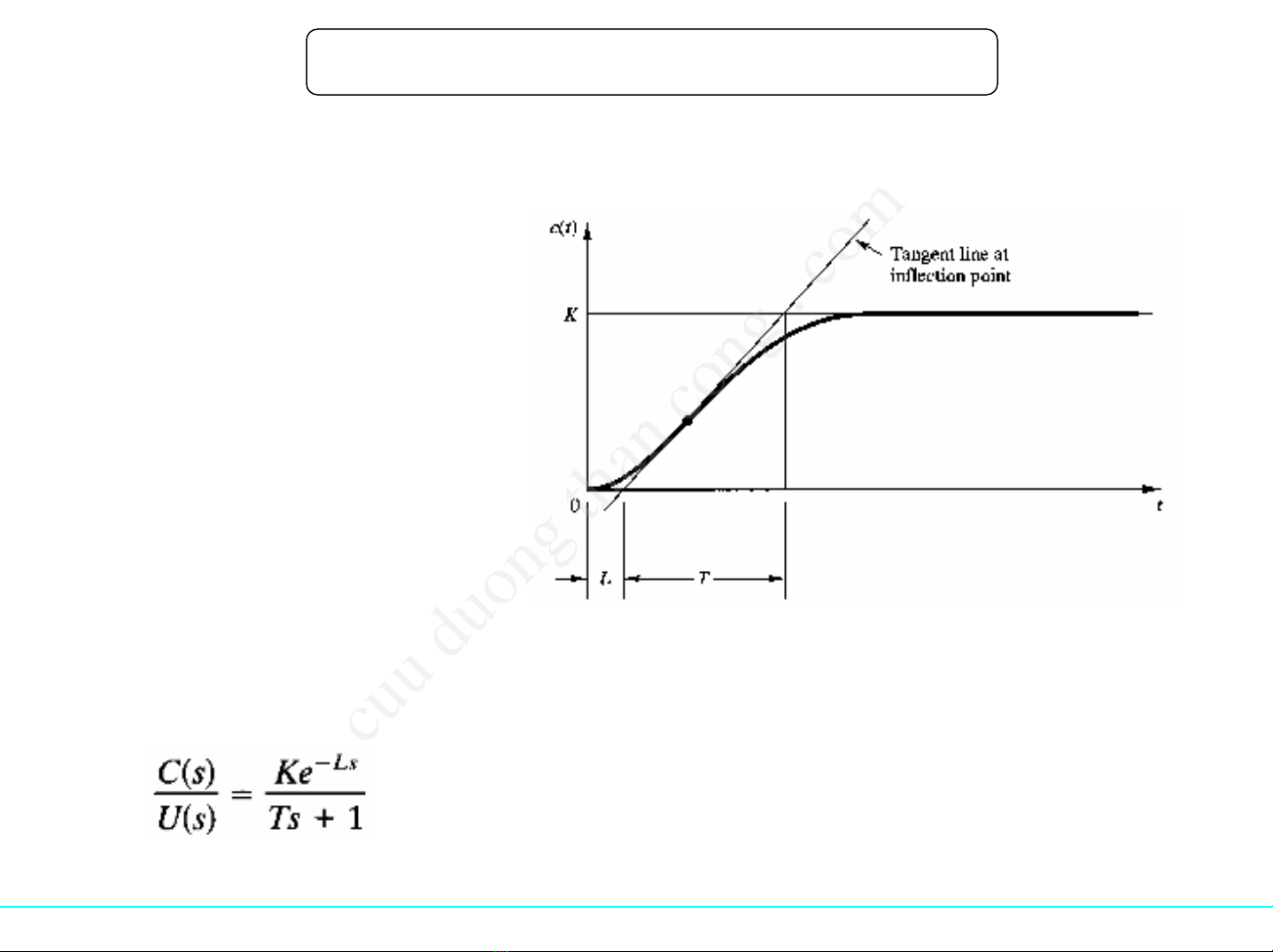
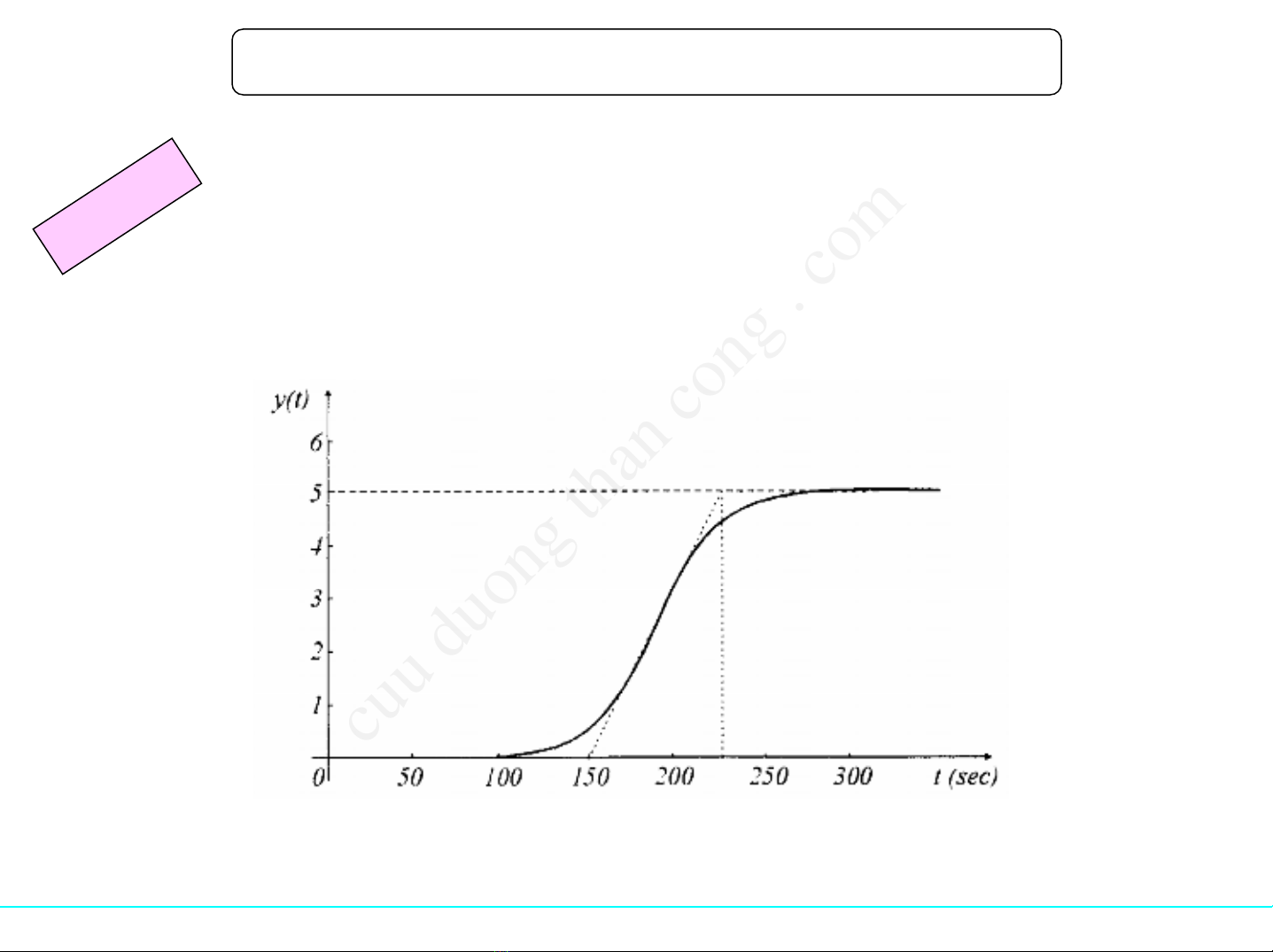
•Xác định bằng thựcnghiệm
đáp ứng bướcnhảycủađối
tượng
•Nếuđáp ứng có dạng hình chữ
S thì áp dụng đượcphương
pháp này
Lý thuyết ĐKTĐ 1 Bộmôn ĐKTĐ-Khoa Điện
cuu duong than cong . com
12-2
Phương pháp Ziegler-Nichols 1
•Từđộthịđó, xác định
các giá trịthờigiantrễL
và hằng sốthờigian T
(xem hình vẽ)
•Khi đóhàm truyềnđạtcủađốitượng có thểxấpxỉvềdạng
Lý thuyết ĐKTĐ 1 Bộmôn ĐKTĐ-Khoa Điện
cuu duong than cong . com
12-3
Phương pháp Ziegler-Nichols 1 (tiếp)
Ziegler và Nichols đãđề xuậtviệcxác định các tham sốcủabộđkPID như
bảng sau:
Lý thuyết ĐKTĐ 1 Bộmôn ĐKTĐ-Khoa Điện
cuu duong than cong . com
12-4
Phương pháp Ziegler-Nichols 1 (tiếp)
Cho đốitượng có đáp ứng bướcnhảyđơnvịnhưhình vẽ. Hãy
xác định Kp, Ti, Td.
Vídụ
Lý thuyết ĐKTĐ 1 Bộmôn ĐKTĐ-Khoa Điện
cuu duong than cong . com