33
CHÖÔNG II : PHAÂN TÍCH MAÏCH TRONG MIEÀN TAÀN SOÁ
Haøm truyeàn ñaït
Trong muïc 1.3 ta ñaõ noùi ñeán vieäc aùp duïng phöông phaùp toaùn töû ñeå phaân tích quaù
trình quaù ñoä trong maïch TTD. Nhö vaäy vôùi taát caû caùc phöông phaùp ñaõ hoïc, ta coù theå xaùc
ñònh ñöôïc taát caû caùc doøng ñieän vaø ñieän aùp treân caùc phaàn töû maïch, ôû moïi traïng thaùi cuûa
maïch. Trong thöïc teá ñoâi khi ngöôøi ta khoâng quan taâm ñeán toaøn boä maïch, maø chæ chuù yù ñeán
1 boä phaän naøo ñoù. Trong tröôøng hôïp nhö vaäy ngöôøi ta tìm ra moät caùch khaùc ñeå moâ taû
maïch, trong ñoù chæ chuù yù ñeán caùc ñaïi löôïng maø ta caàn tìm vaø quan heä cuûa noù vôùi nguoàn
taùc ñoäng. Maïch trong tröôøng hôïp naøy ñöôïc xeùt vôùi khaùi nieäm “ taùc ñoäng – ñaùp öùng” (hay
laø nhaân quaû), cuõng ñoàng nghóa vôùi khaùi nieäm truyeàn ñaït “ Vaøo – Ra”.
II.1. Ñònh nghóa haøm truyeàn ñaït
Giaû thieát raèng , taïi t = 0 maïch ñöôïc taùc ñoäng bôûi nguoàn aùp hay nguoàn doøng (kyù hieäu
laø haøm x(t), vaø ñaïi löôïng caàn xeùt laø doøng hoaëc aùp ôû ñaàu ra kyù hieäu laø y(t)). Vôùi x(t) vaø
y(t) xuaát hieän treân caùc cöïc cuûa maïch ( Hình veõ 1.4.a, b, c).
Khi ñiều kiện đñầu bằng 0, haøm truyền đñạt đñược đñịnh nghĩa nhö sau :
W(P) =
)P(X
)P(Y
Trong ñoù : Y(P) = L [y(t)]
X(P) = L [x(t)].
Haøm truyeàn ñaït laø moät haøm ñaëc tröng cho caùc tính chaát cuûa maïch, moät khi ñaõ bieát
W(P) ta coù theå tìm ñöôïc ñaùp öùng cuûa maïch ñoái vôùi moät taùc ñoäng baát kyø theo bieåu thöùc sau
Y(P) = W(P).X(P)
y(t) = L-1[Y(P)]
Ñeå quan heä giöõa x(t) vaø y(t) laø ñôn trò, thì ñieàu kieän quan troïng laø ñieàu kieän ñaàu
phaûi baèng 0.
Haøm truyeàn cuûa 2 cöïc laø trôû khaùng hay daãn naïp tuøy theo caùc ñaïi löôïng vaøo ra ñöôïc
choïn laø doøng hay aùp. Khi x(t) = u(t) vaø y(t) = i(t), thì haøm truyeàn cuûa 2 cöïc seõ laø daãn naïp.
W(P) =
)P(U
)P(I = Y(P)
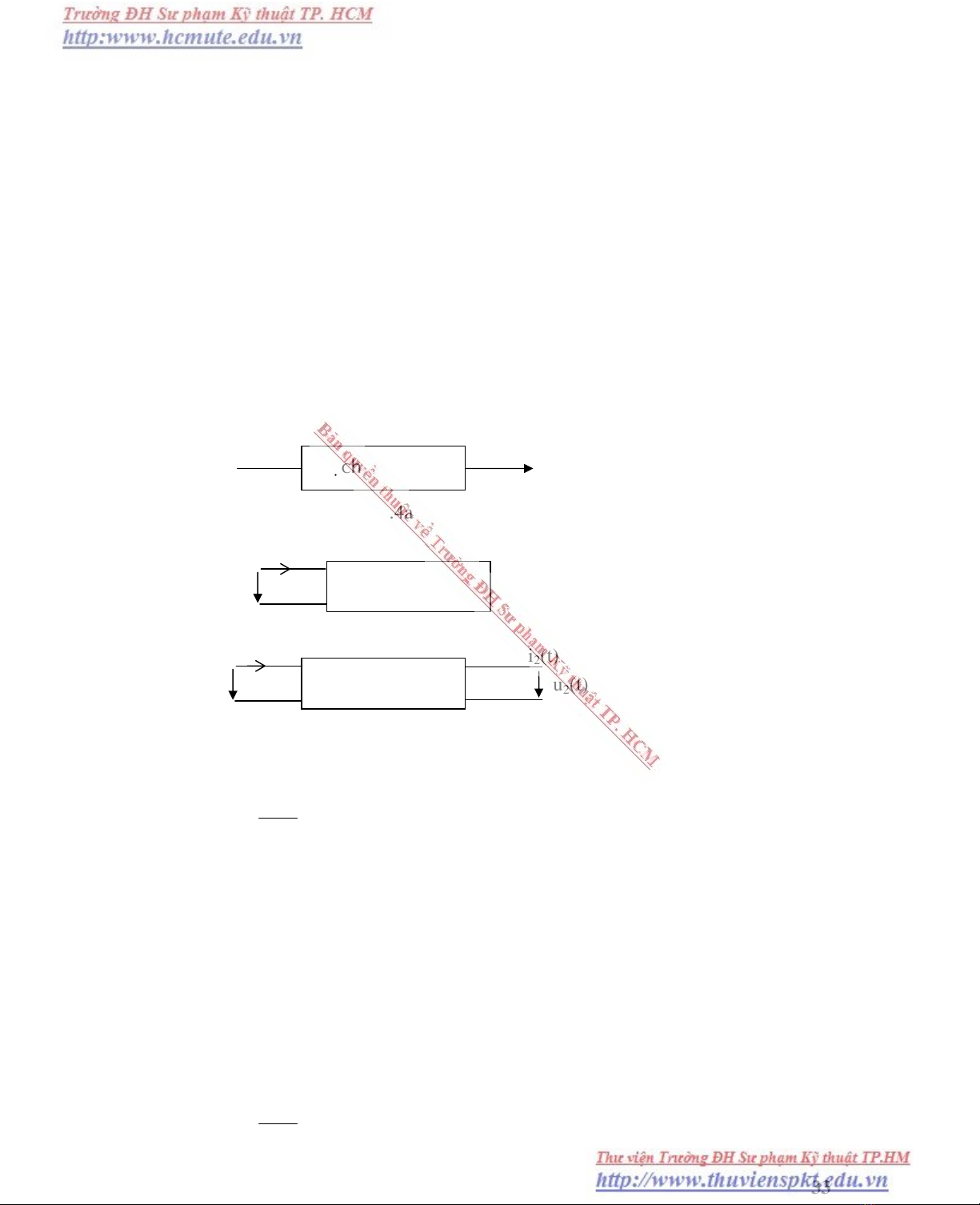
Maïch TTD
x(t) y(t)
H.1.4a
Hai cöïc
i(t)
u1(t)
H.1.4b
Boán cöïc
i1(t)
u1(t)
H.1.4c
i2(t)
u2(t)
34
Khi x(t) = i(t) vaø y(t) = u(t), thì haøm truyeàn cuûa 2 cöïc seõ laø trôû khaùng :
W(P) =
)P(I
)P(U = Z(P)
Chuù thích : ( Töø “haøm truyeàn ñaït” hay “truyeàn ñaït” thöôøng ñöôïc duøng cho maïng hai cöûa
(4 cöïc)vì noù mang yù nghóa truyeàn ñaït tín hieäu. Khi duøng cho 2 cöïc, noù chæ coù yù nghóa laø trôû
khaùng hay daãn naïp cuûa 2 cöïc ñoù.)
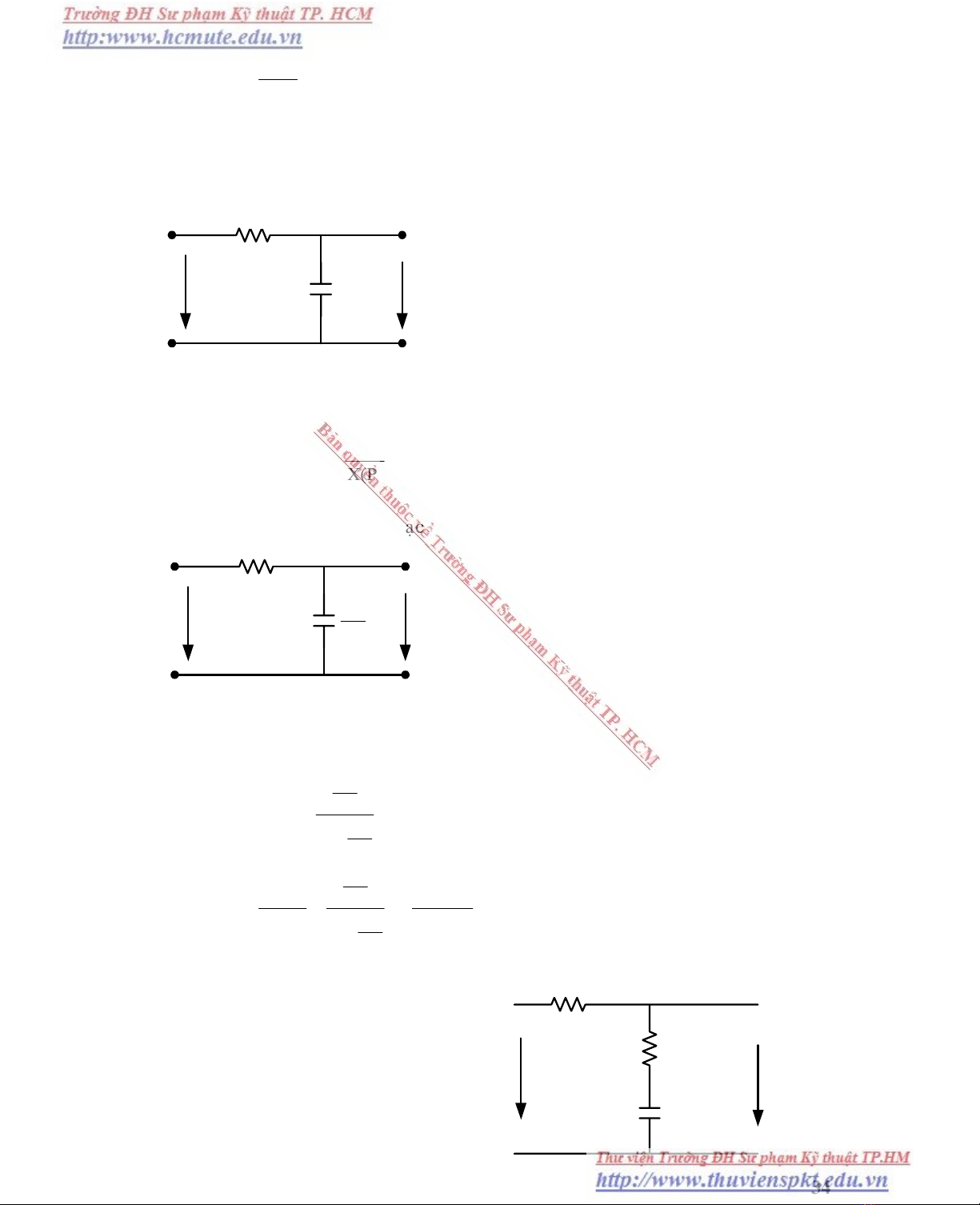
Ví duï : Cho maïch ñieän nhö hình veõ :
u1(t) : tín hieäu vaøo cuûa maïch (x(t))
u2(t) : tín hieäu ra cuûa maïch (y(t))
Tính haøm truyeàn W(P) = )P(X
)P(Y
Giaûi
Böôùc 1: Ñaïi soá hoùa maïch (ñöa maïch veà sô ñoà töông ñöông Laplace)
Ta coù : X(P) = U1(P)
Y(P) = U2(P)
Böôùc 2: Xaùc ñònh haøm truyeàn ñaït aùp :
U
2(P) = U1(P).
CP
R
CP
1
1
+
W(P) =
CP
1
R
CP
1
)P(U
)P(U
1
2
+
= = RCP1
1
+
Ví duï 2 : Cho maïch ñieän nhö hình veõ :
R
)(u
1
t)(u
2
t
C
R
CP
1
)P(U1)P(U2
Ωk9R
1
=
Ω
k
1R
2
=
F0,1µC
1
=
)t(u
1
)t(u
2
35
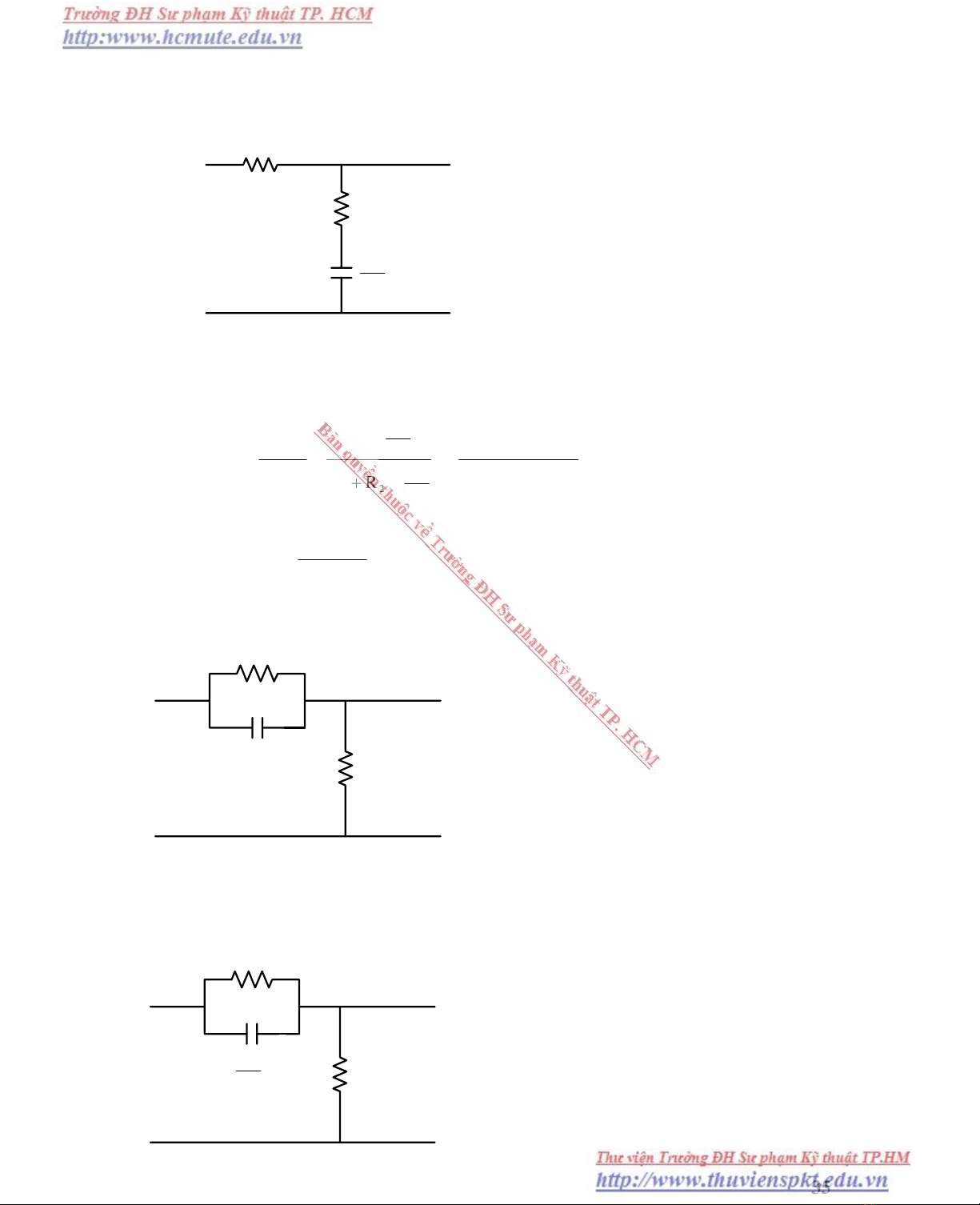
Tính haøm truyeàn ñaït aùp W(P).
Giaûi
Böôùc 1 : Ñaïi soá hoùa maïch (ñöa maïch veà sô ñoà töông ñöông Laplace)
Ta coù : X(P) = U1(P)
Y(P) = U2(P)
Böôùc 2: Xaùc ñònh haøm truyeàn ñaït aùp :
W(P) =
CP
1
RR
CP
1
R
)P(U
)P(U
21
2
1
2
++
+
= = CP)RR(1
CPR1
21
2
++
+
Vaäy W(P) = P101
P101
3
4
−
−
+
+
Ví duï 3 : Cho maïch ñieän nhö hình veõ :
Tính haøm truyeàn W(P)
Giaûi
Böôùc 1 : Ñaïi soá hoùa maïch (ñöa maïch veà sô ñoà töông ñöông Laplace)
Ω
k
9R
1
=
Ω
k
1R
2
=
CP
1
)P(U
1
)P(U
2
1
R
2
R
)P(U
1
)P(U
2
CP
1
1
R
2
R
)t(u1)t(u2
C
36
Böôùc 2: Xaùc ñònh haøm truyeàn ñaït aùp :
)P(U.
CP
1
R
CP
1
R
R
R
)P(U 1
1
1
2
2
2
+
+
=
W(P) =
1221
12
1
2RRCPRR
)1CPR(R
)P(U
)P(U
++
+
=
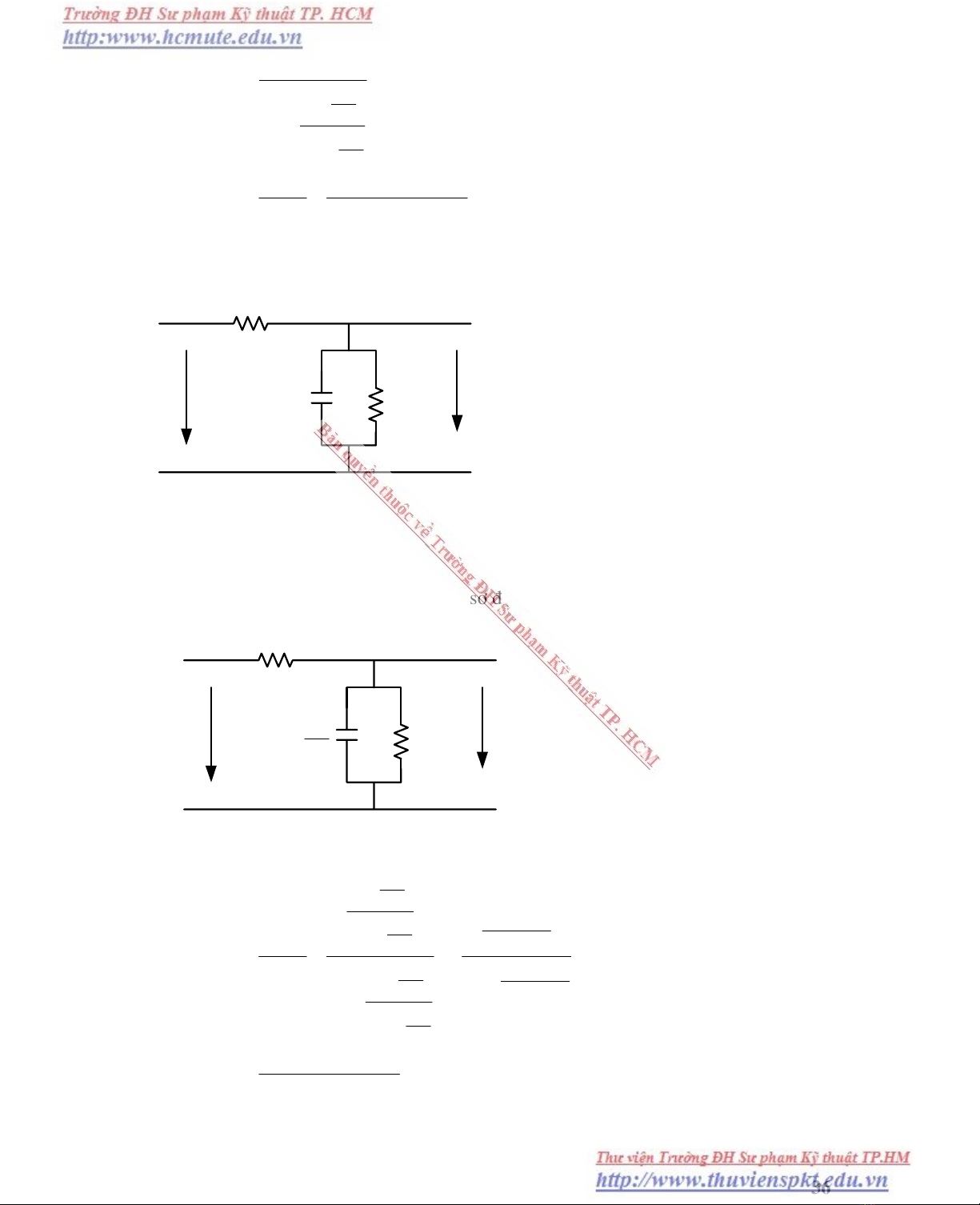
Ví Duï 4 : Cho maïch ñieän nhö hình veõ sau :
Tính haøm truyeàn W(P)
Giaûi
Böôùc 1 : Ñaïi soá hoùa maïch (ñöa maïch veà sô ñoà töông ñöông Laplace)
Böôùc 2: Xaùc ñònh haøm truyeàn ñaït aùp
W(P) =
CP
1
R
CP
1
R
R
CP
1
R
CP
1
R
)P(U
)P(U
2
2
1
2
2
1
2
+
+
+
= =
1CPR
R
R
1CPR
R
2
2
1
2
2
+
+
+
W(P) =
1221
2RRCPRR
R
++
1
R
2
R
)P(U
1
)P(U
2
CP
1
1
R
2
R
)t(u1
)t(u
2
C
37
II.2.Bieåu dieãn ñoà thò cuûa haøm truyeàn
II.2.1. Ñaëc tuyeán logarit – taàn soá logarit
Trong thöïc teá ngöôøi ta thöôøng quan taâm ñeán ñaëc tuyeán bieân ñoä W(jω); bôûi vì noù deã
ño löôøng vaø noù cho ta bieát nhieàu tính chaát cuûa maïch ñoái vôùi taàn soá.
Khaùi nieäm veà Bel vaø decibel
bel → B
decibel → dB
1b = 10db
Laø ñôn vò ñeå ño möùc taêng giaûm cuûa tín hieäu
vaøo
ra
P
P
lg → [b]
1b → {Pr = 10 PV}
10
vaøo
ra
P
P
lg → [db]
+ 10db → Pr = 10 PV
+ 20db → Pr = 100 PV
0db → Pr = PV
- 10db → Pr = 10
PV
- 20db → Pr = 100
PV
2
V
r
V
rU
U
P
P
= ⇒ 10lg
V
r
P
P = 10lg
2
V
r
U
U
db = 20lg
V
r
U
U (db)
Thoâng thöôøng ñaëc tuyeán taàn soá ñöôïc vieát döôùi daïng :
W(P) = PT+1
1
hay W(jω) = ωTj1
1
+
Trong ñoù P = jω
Tjω : soá phöùc
Modun W(jω)
Argumen ϕ(ω)
II.2.2. Giaûn ñoà Bode
Ví duï ta khaûo saùt söï bieán thieân cuûa haøm truyeàn :
W(jω) = ωTj1
1
+
Pvaøo Pra








![Mạch Điện Điện Trở: [Thêm Mô Tả Chi Tiết Hấp Dẫn Tại Đây]](https://cdn.tailieu.vn/images/document/thumbnail/2013/20130917/butmaulam/135x160/1561226_146.jpg)




![Ngân hàng câu hỏi ôn tập Anten và truyền sóng [Năm]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250115/sanhobien01/135x160/18471768473368.jpg)




![Đề cương ôn tập Kỹ thuật điện [năm học] chuẩn nhất](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250613/laphong0906/135x160/48561768293690.jpg)



![Bài tập lớn Truyền động điện [chuẩn SEO]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250612/minhquan0690/135x160/70681768205796.jpg)
![Mạch khuếch đại ghép tầng điện tử cơ bản: Bài tập lớn [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250612/minhquan0690/135x160/49651768206643.jpg)


