Tuan V. Nguyen
Senior Principal Research Fellow, Garvan Institute of Medical Research
Professor, UNSW School of Public Health and Community Medicine
Professor of Predictive Medicine, University of Technology Sydney
Adj. Professor of Epidemiology and Biostatistics,
School of Medicine Sydney, University of Notre Dame Australia
Phân tích dữ liệu và ứng dụng | Đại học Dược Hà Nội | 12/6 to 17/6/2019 © Tuan V. Nguyen
Mô hình hồi qui logistic (logistic regression)
• Ví dụ dẫn nhập
• Khái niệm odds, logit, và mô hình hồi qui logistic
• Ước tính và R
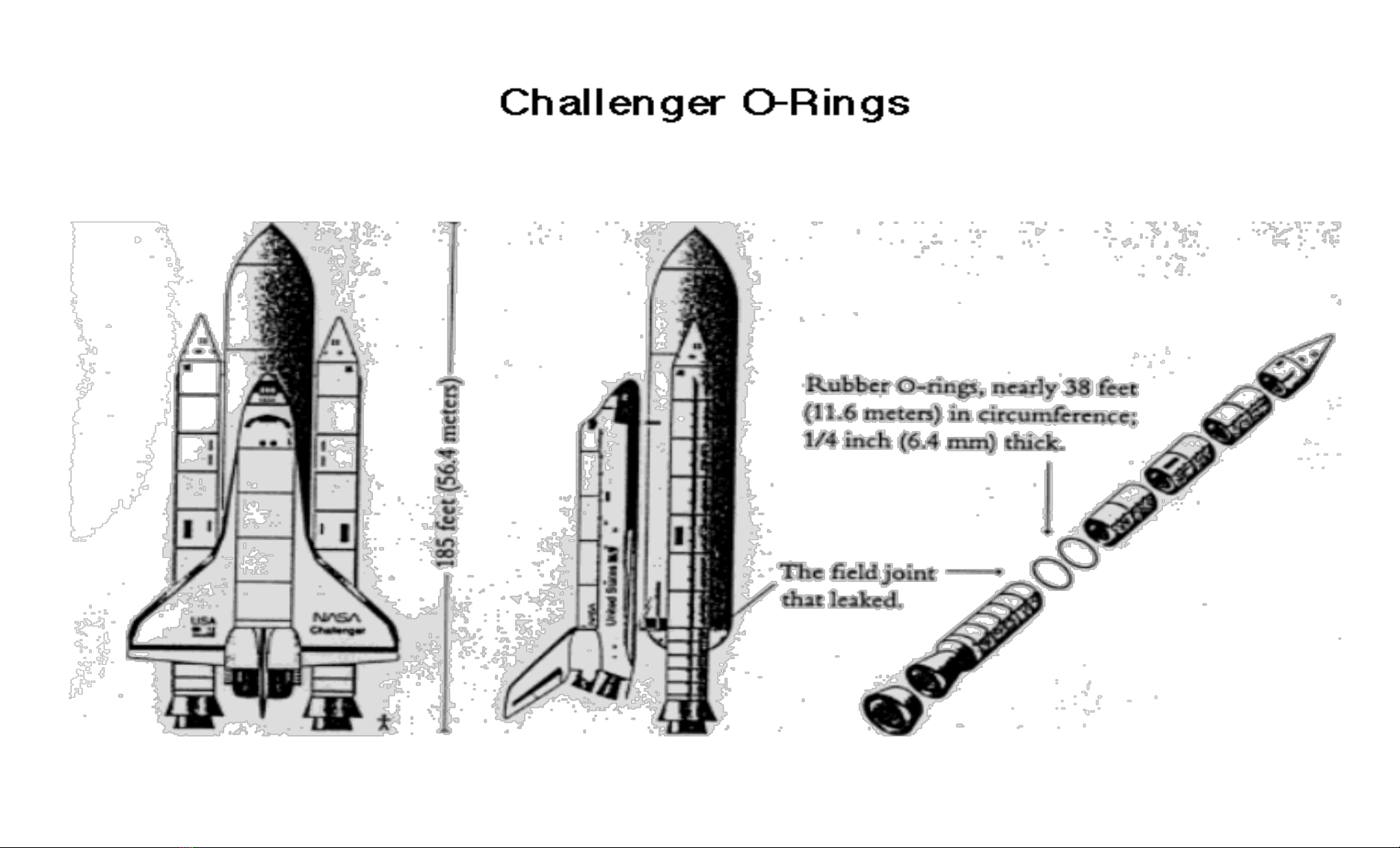
The Challenger shuttle disaster
Flight
Temp
Damage
STS
-1
66
0
STS
-2
70
1
STS
-3
69
0
STS
-4
80
STS
-5
68
0
STS
-6
67
0
STS
-7
72
0
STS
-8
73
0
STS
-9
70
0
STS 41B
57
1
STS 41C
63
1
STS 41D
70
1
STS 41G
78
0
STS 51A
67
0
STS 51C
53
1
STS 51D
67
0
Flight
Temp
Damage
STS 51B
75
0
STS 51G
70
0
STS 51F
81
0
STS 51I
76
0
STS 51J
79
0
STS 61A
75
1
STS 61B
76
0
STS 61C
58
1
Temp = c(66, 70, 69, 80, 68, 67, 72, 73, 70, 57, 63,
70, 78, 67, 53, 67, 75, 70, 81, 76, 79, 75, 76, 58)
Damage = c(0, 1, 0, ., 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0,
0, 0, 0, 0, 0, 1, 0, 1)
Nghiên cứu bệnh tiểu đường (type 2 diabetes)
•Nghiên cứu cắt ngang trên 3155 cá nhân
• Outcome: chẩn đoán tiểu đường
• Yếu tố nguy cơ: tuổi, giới tính, huyết áp, vòng eo, vòng mông, cân nặng,
tỉ trọng cơ thể (BMI)
• Câu hỏi 1: BMI có liên quan đến bệnh tiểu đường?
• Câu hỏi 2: Yếu tố nào có liên quan đến tiểu đường?
• Câu hỏi 2: Có thể xây dựng mô hình tiên lượng nguy cơ mắc bệnh?