3.1. Hệ toạ độ thuần nhất.
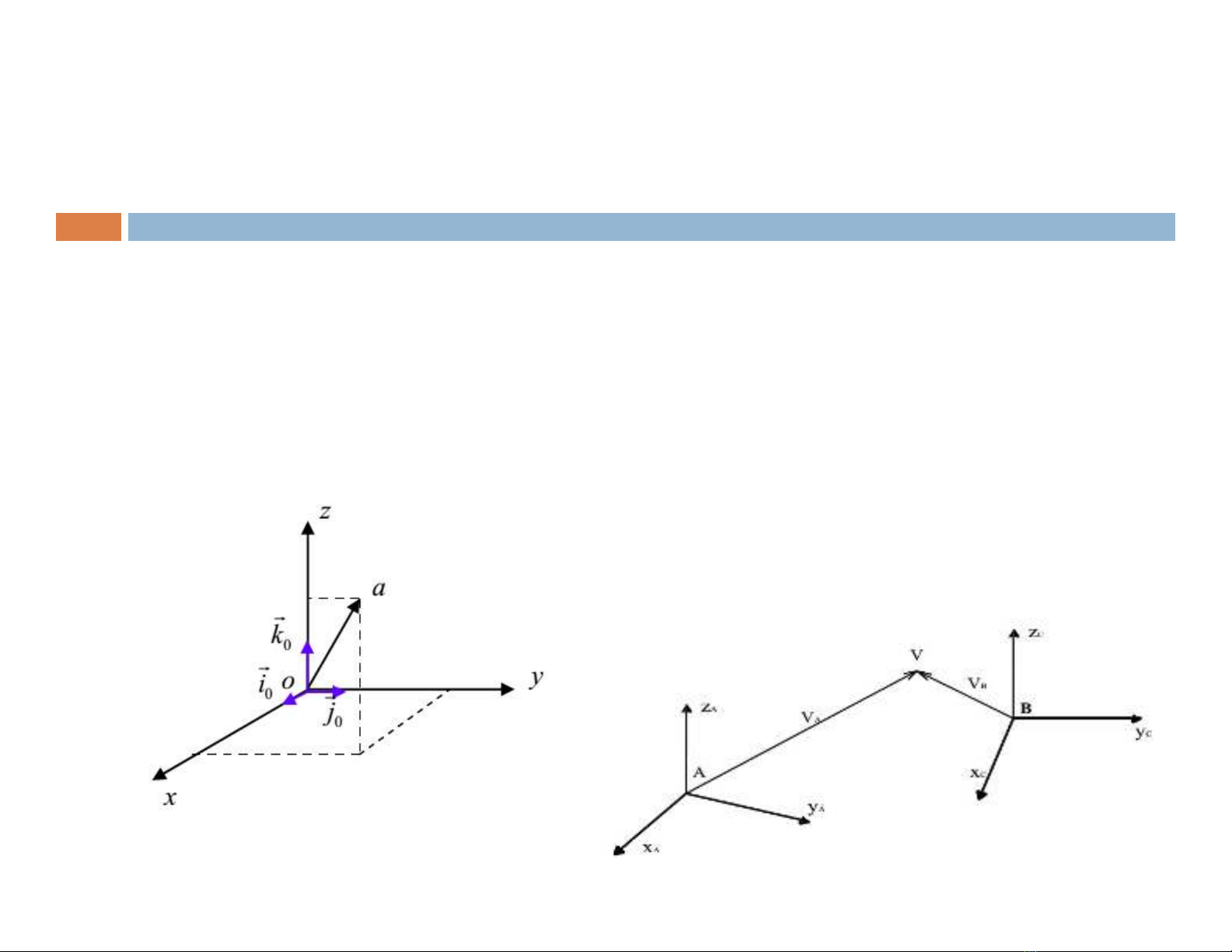
Để biểu diễn 1 điểm trong không gian 3 chiều, người ta
dùng vector điểm ( Point Vector)
Tuỳ thuộc hệ qui chiếu được chọn mà 1 điểm trong không
gian có thể được biểu diễn bằng các vector điểm khác nhau
CHƯƠNG III:
ĐỘNG HỌC ROBOT
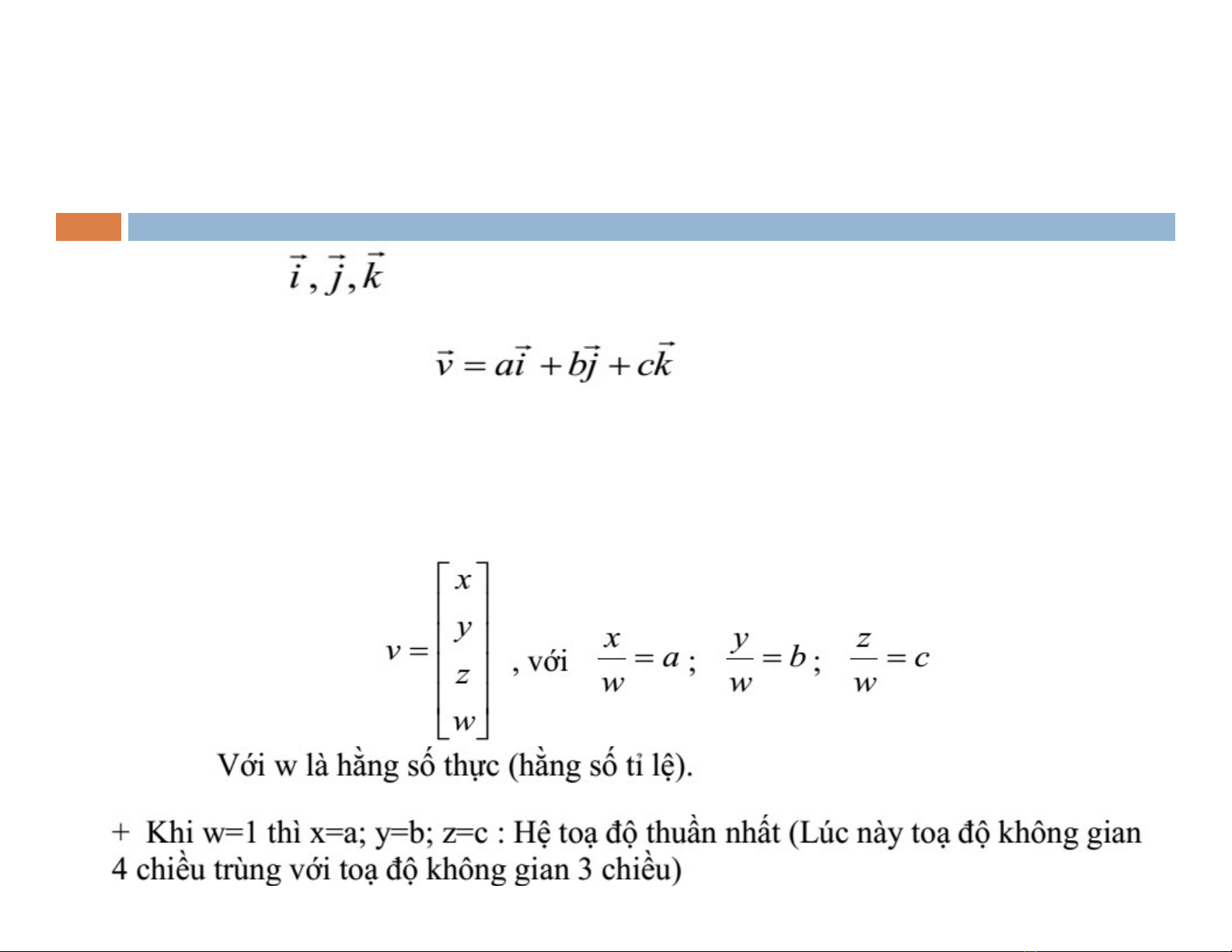
Nếu gọi các vector định vị của hệ toạ độ nào đó thì vector điểm
Với a,b,c là toạ độ vị trí của điểm v
Nếu đồng thời quan tâm đến vị trí và định hướng ta phải
biểu diễn trong không gian 4 chiều
CHƯƠNG III:
ĐỘNG HỌC ROBOT

CHƯƠNG III:
ĐỘNG HỌC ROBOT
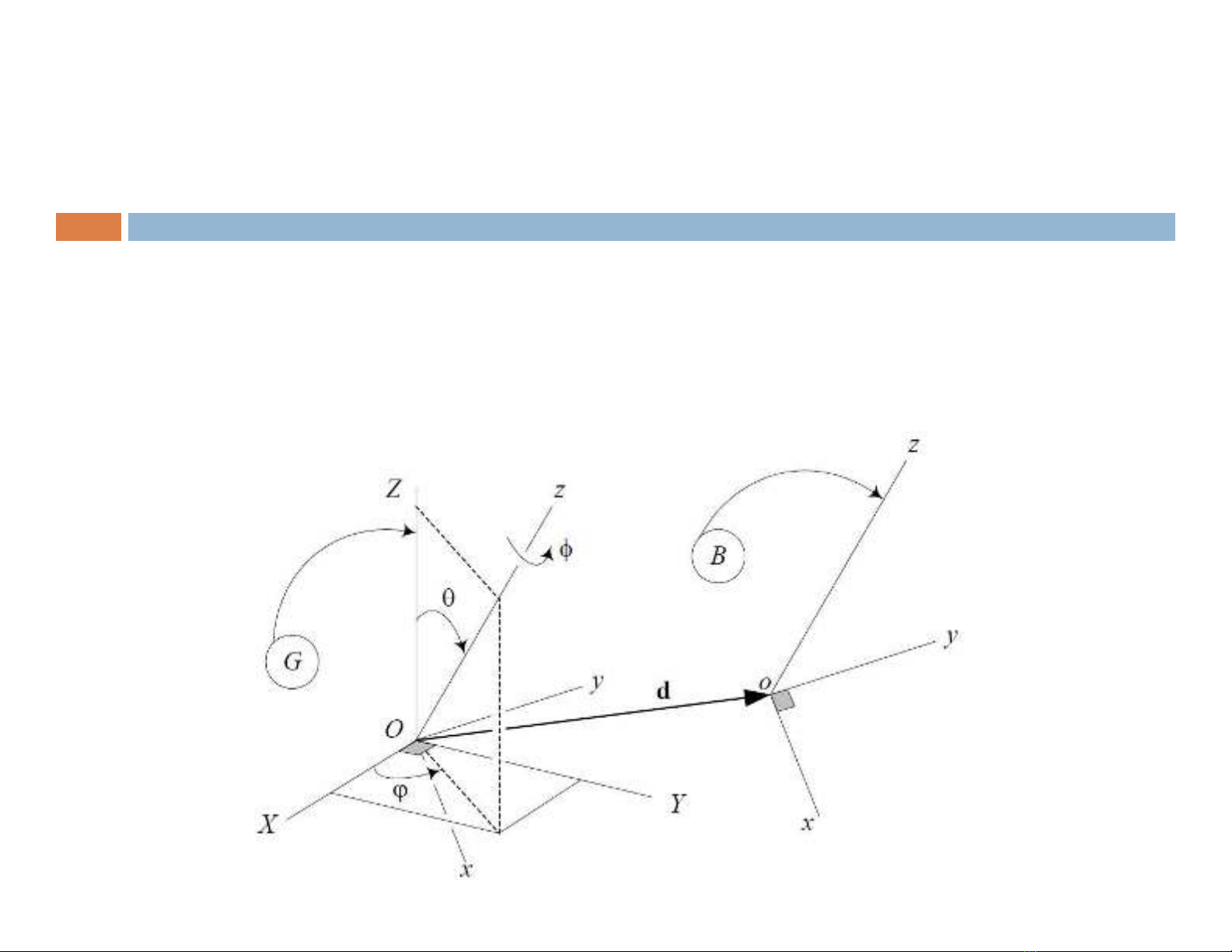
Chuyển động vật rắn
Xét một vật rắn với hệ tọa độ B(oxyz) đang di chuyển so với hệ tọa độ gốc G(OXYZ).
Vật rắn có thể quay trong hệ tọa độ gốc, trong khi điểm o của khung B có thể dịch
chuyển tương đối so với điểm gốc O của G như hình:
CHƯƠNG III:
ĐỘNG HỌC ROBOT

Gọi là tọa độ của P trên hệ tọa độ vật B
là vị trí tương đối của điểm gốc di động o so với điểm gốc cố định O
Tọa độ của P trong hệ tọa độ gốc được tính theo công thức sau:
Với:
CHƯƠNG III:
ĐỘNG HỌC ROBOT


























