Baì Giảng Sức Bền Vật Liệu
Chương 9:Xoắn thuần túy thanh thẳng GV :Lê đức Thanh
1
Chương 9
XOẮN THUẦN TÚY THANH THẲNG.
1-Định nghĩa:
Thanh chịu xoắn thuần túy khi trên các mặt cắt ngang chỉ
có một thành phần nội lực là mômen xoắn Mz (H.9.1).
Dấu của nội lực Mz: Mz 0 khi từ ngoài nhìn vào mặt cắt
thấy Mz quay cùng kim đồng hồ và ngược lại.
Ngoại lực: Gồm các ngẫu lực mômen xoắn tâp trung Mo
(Nm) hay phân bố m(Nm/m), nằm trong mặt phẳng vuông
góc trục thanh.
Thực tế thường gặp: các trục truyền động, thanh chịu lực không gian, dầm đỡ ô
văng...
2- Biểu đồ nội lực mômen xoắn Mz
Biểu đồ mômen xoắn được vẽ bằng phương pháp mặt cắt.
Từ điều kiện cân bằng tĩnh học: M/OZ = 0 suy ra nội lực Mz trên mặt cắt.
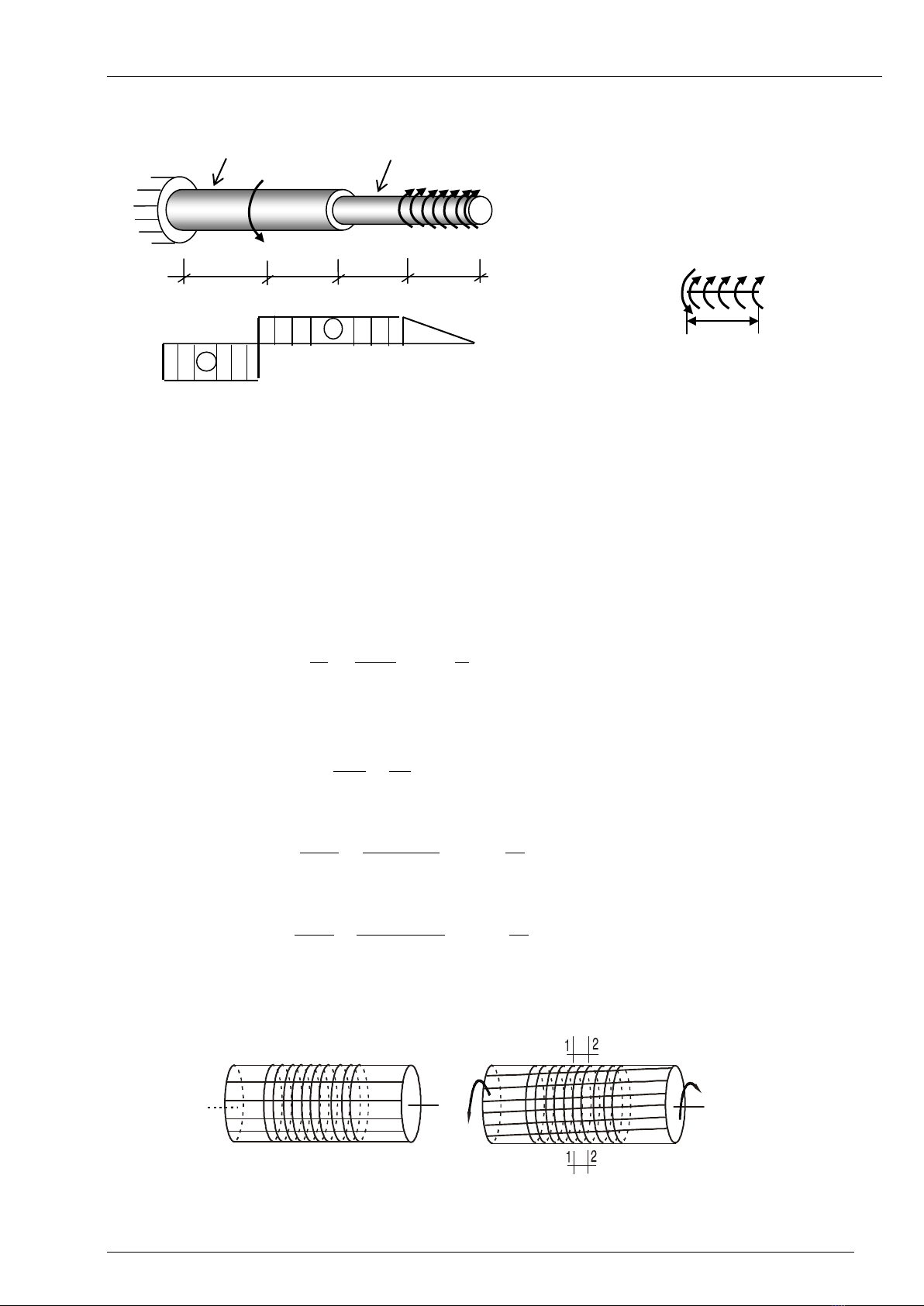
Thí dụ 1: Vẽ biểu đồ Mz
Thực hiện mặt cắt 1-1 trong đoạn AB, xét cân bằng phần bên trái của mặt cắt, ngoại lực
là ngẫu lực xoắn MA nội lực tại mặt cắt 1-1 là mômen xoắn Mz vẽ theo chiều dương.
Lập phương trình cân bằng tỉnh học:
M / z = 0 Mz = MA= 5Nm (Momen ngoại lực tập trung nội lực không phụ thuộc z)
Tương tự cho các mặt cắt trong đoạn BK và KC và biểu đồ được vẽ như hình trên
(Chú ý tại mặt cắt có Mo tập trung trên biểu đồ Mz sẽ có bước nhảy và giá trị bằng
momen tập trung đó, biểu đồ hằng số trong từng đoạn không phụ thuộc z)
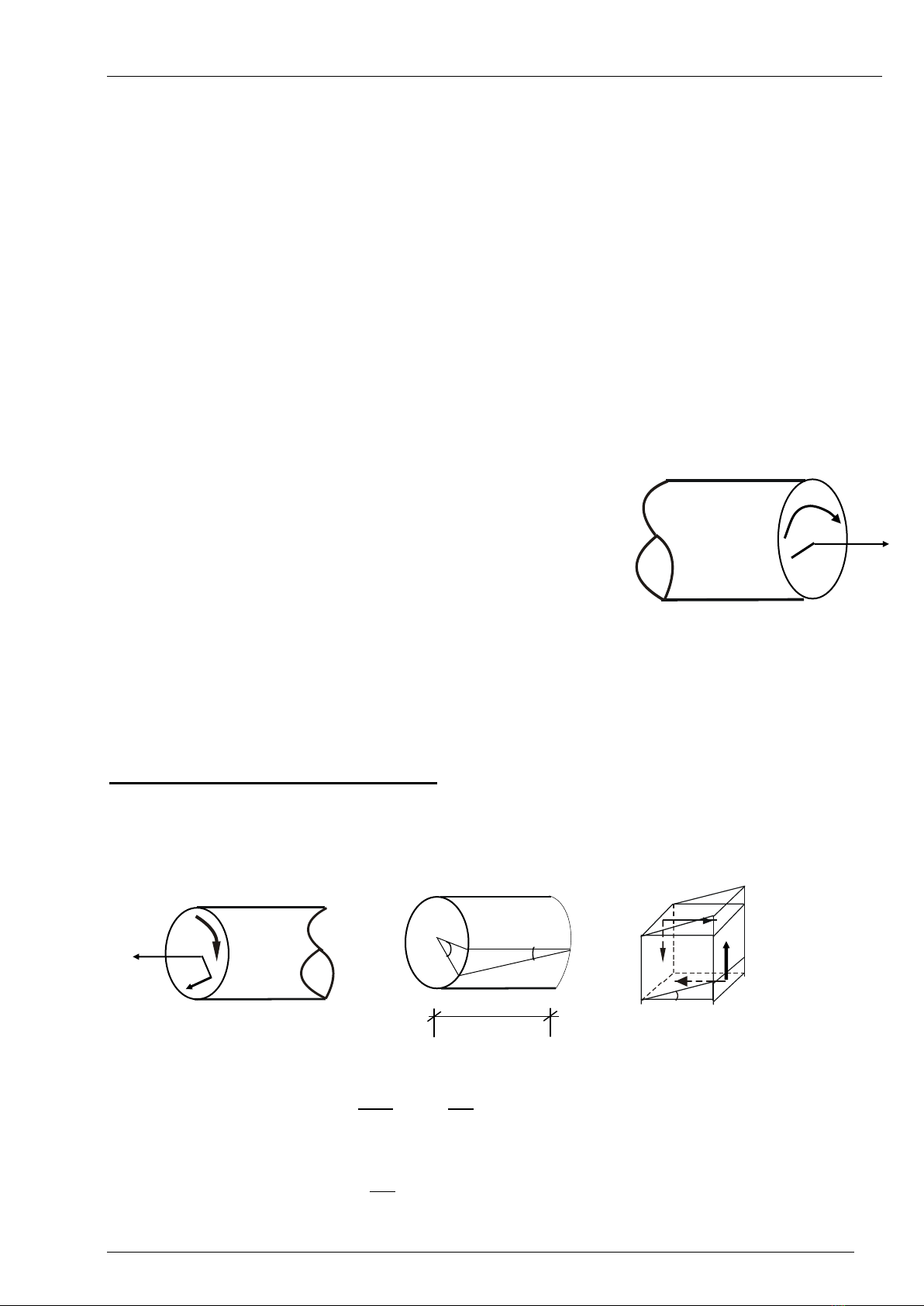
Thí dụ 2:
Cho trục có tiết diện thay đổi, đoạn AK có momen phân bố đều m hằng số và moment
tập trung như hình vẽ. Vẽ biểu đồ nội lực Mz
Thực hiện mặt cắt trong đoạn AK như hình dưới, ta thấy biểu đồ Mz bậc 1trong đoạn
AK và các đoạn khác giống như thí dụ đã vẽ trên
y
z
Mz
x
O
H. 9.1
_
+
5Nm
15N-m
A
K
C
L
M
A
=5N-m
L
M
B
=20N-m
M
C
=10N-m
B
MK=25N-m
L
L
01
B
M
A
=10Nm
Mz
z1
1
1
+
M
C
=10N-m
Baì Giảng Sức Bền Vật Liệu
Chương 9:Xoắn thuần túy thanh thẳng GV :Lê đức Thanh
2
Đoạn AK
3. Công thức chuyển đổi công suất động cơ W(N-m/s) ra ngẫu lực xoắn (mômen
xoắn ngoại lực M0 (N.m) trên trục.
Khi tính toán các trục truyền động, thường ta biết công suất truyền của môtơ tính
bằng mã lực (CV) hay kilôóat(kW) và tốc độ trục quay bằng n (vòng/phút), do đó cần
chuyển đổi công suất truyền ra ngẫu lực xoắn tác dụng lên trục.
Giả sử có một ngẫu lực xoắn Mo (N.m) tác dụng làm trục quay một góc
(radian)
trong thời gian t (giây), công sinh ra là:
A = Mo.
Công suất là:
oo
oM
t
M
t
M
t
A
W
trong đó: - là vận tốc góc (rad/s), đơn vị của công suất là N.m/s.
Gọi n là số vòng quay của trục trong một phút (vòng/phút), ta có:
3060
2nn
a) Nếu W tính bằng mã lực (CV, HP); 1mã lực = 750Nm/s = 0,736 kW:
)Nm(7162
.750.3030
n
W
n
W
n
W
Mo
b) Nếu W tính bằng kilôwat (KW), 1 KW 1020 N.m/s:
)Nm(9740
.1020.30
.
30
n
W
n
W
n
W
Mo
. XOẮN THUẦN TUÝ THANH THẲNG TIẾT DIỆN TRÒN
dz
a)
b)
Mz
H.9.2
Mz
K
a
a
a=50cm
40Nm
m=20Nm/m
C
D
B
d2=10cm
d1=6cm
a
10Nm
30Nm
+
-
z
m
Mz
0 < z < a
Mz-mz=0
Mz= mz
A
Baì Giảng Sức Bền Vật Liệu
Chương 9:Xoắn thuần túy thanh thẳng GV :Lê đức Thanh
3
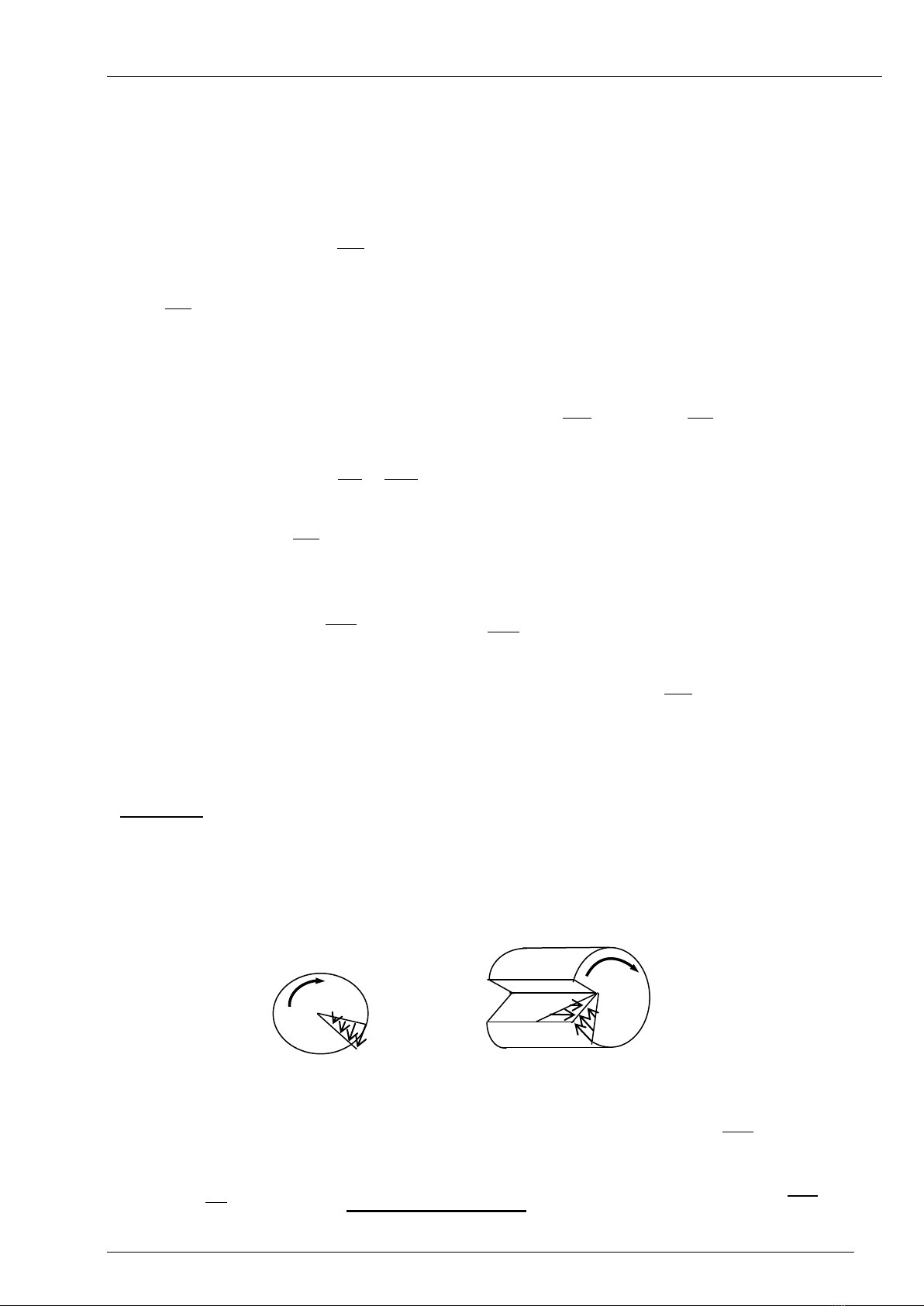
1- Thí nghiệm - Nhận xét
Xét một thanh thẳng tiết diện tròn, trên mặt ngoài vạch những đường song song và
những đường tròn thẳng góc với trục, tạo thành lưới ô vuông (H.9.2.a).
Tác dụng lên hai đầu thanh ngẫu lực xoắn Mz ngược chiều, ta thấy trục thanh vẫn
thẳng, chiều dài thanh không đổi, những đường tròn thẳng góc với trục vẫn tròn và
thẳng góc với trục, những đường song song với trục thành những đường xoắn ốc, lưới ô
vuông thành lưới bình hành (H.9.2.b).
2- Các giả thiết : Trong quá trình biến dạng :
a) Mặt cắt ngang vẫn phẳng, thẳng góc với trục thanh và khoảng cách không đổi
b) Các bán kính vẫn thẳng và chiều dài không đổi
c) Các thớ dọc không ép và đẩy lẩn nhau
3- Ưng suất trên mặt cắt ngang.
Tính ứng suất tại một điểm bất kỳ trên mặt cắt ngang có
bán kính đến tâm 0 (H.9.3).Theo thí nghiệm trên ta nhận
thấy, biến dạng của thanh chịu xoắn thuần túy chỉ là sự
xoay tương đối giữa các mặt cắt ngang quanh trục z.
Theo giả thiết a) không có biến dạng dài theo phương
dọc trục, theo giả thiết c) các thớ dọc không tác dụng với
nhau nên không có ứng suất pháp tác dụng lên các mặt của
phân tố.
Do giả thiết b), mọi bán kính vẫn thẳng nên không có ứng suất tiếp hướng tâm
Như vậy, trên mặt cắt ngang của thanh chịu xoắn thuần túy chỉ tồn tại ứng suất tiếp
theo phương vuông góc bán kính và cùng chiều với Mz gọi là
và phân tố đang xét ở
trạng thái ứng suất trượt thuần túy (H.9.4).
Để xét biến dạng xoắn ta tách phân tố hình trụ tròn có bán kính qua điểm muốn tính
và đoạn AB bằng dz. Giã sữ mặt cắt tại B đứng yên, mặt cắt tại A xoay một góc d từ A
đến A/ theo chiều Mz như sau : Gọi là góc trượt
Từ (H.9.3), ta có:
Tan
=
dz
d
AB
AA
(a)
Áp dụng định luật Hooke về trượt cho phân tố này, ta có:
dz
d
GG
p
(b)
Gọi dA là một diện tích vô cùng bé bao quanh điểm đang xét, thì
.dA là lực tiếp
H. 9.4
Phân tố trượt thuần túy
H. 9.3
z
Mz
O
z
z
0
A
d
dz
A/
B
H. 9.3
z
Mz
O
z
Baì Giảng Sức Bền Vật Liệu
Chương 9:Xoắn thuần túy thanh thẳng GV :Lê đức Thanh
4
tuyến tác dụng trên diện tích đó và
.dA.
là mômen của lực
dA đối với tâm O.
Tổng các mômen này phải bằng Mz, nên ta có thể viết:
A
pz dAM
(c)
(b) vào (c)
A
zdA
dz
d
GM
(d)
Vì :
dz
d
là hằng số đối với mọi điểm thuộc mặt cắt A, nên ta có thể đưa ra ngoài dấu
tích phân, khi đó tích phân
A
dA.
.2
chính là mômen quán tính cực (đối với một điểm) Ip
của mặt cắt ngang đối với tâm O, ta được:
p
A
zI
dz
d
GdA
dz
d
GM
2
(e)
từ (e) ta có :
GI
M
dz
dz
(f)
Có thể thấy rằng :
dz
d
chính là góc xoắn trên một đơn vị chiều dài (còn gọi là góc
xoắn tỉ đối) đơn vị (rad/m).
Đặt :
dz
d
, ta có:
GI
Mz
từ (b) và (f) ta suy được công thức tính ứng suất tiếp :
I
Mz
Trong đó Mz là nội lực trên mặt cắt, là khoảng cách từ điểm muốn tính ứng suất đến
tâm 0, và IP là momen quán tính đối với tâm 0 của mặt căt ngang.
Nhận xét :
-Ứng suất tiếp thay đổi theo quy luật bậc nhất, bằng không tại tâm 0 và cực đại tại
những điểm trên chu vi ( =R), và cùng chiều với Mz
- Biểu đồ phân bố ứng suất tiếp tại mọi điểm trên mặt cắt ngang
Trên H.9.7.b, thể hiện ứng suất tiếp đối ứng trên các mặt cắt chứa trục.
Ứng suất tiếp cực đại ở các điểm trên chu vi (
= bán kính R)
R
I
Mz
max
đặt:
R
I
W
; Wp : gọi là mômen chống xoắn của mặt cắt ngang
W
Mz
max
max
0
M
z
M
z
Hình 9.5a
Hình 9.5b
max
max
0

Baì Giảng Sức Bền Vật Liệu
Chương 9:Xoắn thuần túy thanh thẳng GV :Lê đức Thanh
5
* Với tiết diện tròn đặc và D là đường kính:
3
33
20
162D
DR
R
I
W,
* Với tiết diện tròn rỗng:
)(,)(
)( 434
344
1201
16
1
32
1
D
D
R
D
R
I
W
trong đó:
là tỷ số giữa đường kính trong và đường kính ngoài (
= d/D).
4- Công thức tính biến dạng khi xoắn
Góc xoắn tương đối giữa hai mặt cắt cách nhau dz là :
dz
GI
M
dz
Góc xoắn tương đối giữa hai mặt cắt cách nhau một đoạn dài L là:
L
o
L
o
zdz
GI
M
d
* Khi đoạn thanh có
p
z
GI
M
là hằng số
p
z
GI
LM
* Khi thanh gồm nhiều đoạn, mỗi đoạn có
p
z
GI
M
là hằng số:
i
i
z
GI
LM )(
Góc xoắn
được quy ước dương theo chiều dương của Mz và thứ nguyên Radian
5- Tính toán thanh tròn chịu xoắn thuần tuý:
Điều kiện bền:
nW
M
P
z0
max
với:
o - là ứng suất tiếp nguy hiểm của vật liệu, xác định từ thí nghiệm
n : là hệ số an toàn.
+ Nếu tính theo thuyết bền ứng suất tiếp (TB3):
2
][
max
+ Nếu tính theo thuyết bền thế năng biến đổi hình dạng(TB4):
3
][
max
Điều kiện cứng:
max [
]
[
]: Góc xoắn tỷ đối cho phép, được cho từ các sổ tay kỹ thuật,
đơn vị của [
] là (radian/ đơn vị chiều dài, hay độ/ đơn vị chiều dài).
Công thức qui đổi:
3602
/0/ mmrad
Từ điều kiện bền và cứng ta có ba bài toán cơ bản:
- Kiểm tra điều kiện bền, cứng.
- Xác định tải trọng cho phép.
- Xác định đường kính.
Thí du 3:
Cho thanh có tiết diện tròn đường kính thay đổi. Đoạn BC có d1=8cm, đoạn CD có d2 =
6 cm.
a) Vẽ biêu đồ momen xoắn Mz


























