
1
22 October 2012 1
Toán rời rạc (4):
ĐỒ THỊ EULER VÀ ĐỒ THỊ
HAMILTON
Ts. Hoàng ThịThanh Hà
Khoa Thống kê –Tin học
Trường Đại học Kinh tế
Đại họcĐà Nẵng
22 October 2012 2
Nội dung
1. ĐƯỜNG ĐI EULER VÀ ĐỒ THỊ EULER
2. ĐƯỜNG ĐI VÀ ĐỒ THỊHAMILTON
22 October 2012 3
ĐƯỜNG ĐI & ĐỒ THỊ EULER
Có thểcoi năm 1736 là năm khai sinh lý thuyếtđồ thị,
với việc công bốlời giải “bài toán vềcác cầuở
Konigsberg” của nhà toán học lỗi lạc Euler (1707-
1783)
Thành phốKonigsberg thuộc Phổ(nay gọi là
Kaliningrad thuộc Nga) được chia thành bốn vùng
bằng các nhánh sông Pregel, các vùng này gồm hai
vùng bên bờsông, đảo Kneiphof và một miền nằm
giữa hai nhánh của sông Pregel. Vào thếkỷ18, người
ta xây bảy chiếc cầu nối các vùng này với nhau.
22 October 2012 4
ĐƯỜNG ĐI & ĐỒ THỊ EULER
Sông Pregel và 7 chiếc cầu nối các vùng này với nhau.
2
22 October 2012 5
ĐƯỜNG ĐI & ĐỒ THỊ EULER
“Có thểnào đi dạo qua tất cảbảy cầu, mỗi cầu chỉmột
lần thôi không?”
Nếu ta coi mỗi khu vực A, B, C, D nhưmộtđỉnh và
mỗi cầu qua lại 2 khu vực là 1 cạnh nối hai đỉnh thì ta
có sơ đồ của Konigsberg là mộtđađồ thịG:
22 October 2012 6
ĐƯỜNG ĐI & ĐỒ THỊ EULER
Bài toán tìm đường đi qua tất cảcác cầu, mỗi cầu chỉ
qua một lần có thể được phát biểu lại bằng mô hình
này nhưsau: Có tồn tại chu trình đơn trong đađồ thị
G chứa tất cảcác cạnh?
22 October 2012 7
ĐƯỜNG ĐI & ĐỒ THỊ EULER
a) ĐN1: Đường đi và đồ thịEuler
i) Đường đi Euler là đường đi qua tất cảcác cạnh (cung) mỗi cạnh
đúng một lần.
Chu trình Euler là chu trình đi qua tất cảcác cạnh củađồ thịmỗi cạnh
đúng một lần.
ii) Đồ thị được gọi là đồ thịEuler nếu nó có chu trình Euler
iii) Đồ thị được gọi là đồ thịnửa Euler nếu nó có dường đi Euler
Nhận xét: Đường đi (t.ưchu trình ) Euler là đường đi (t.ưchu trình) đơn
22 October 2012 8
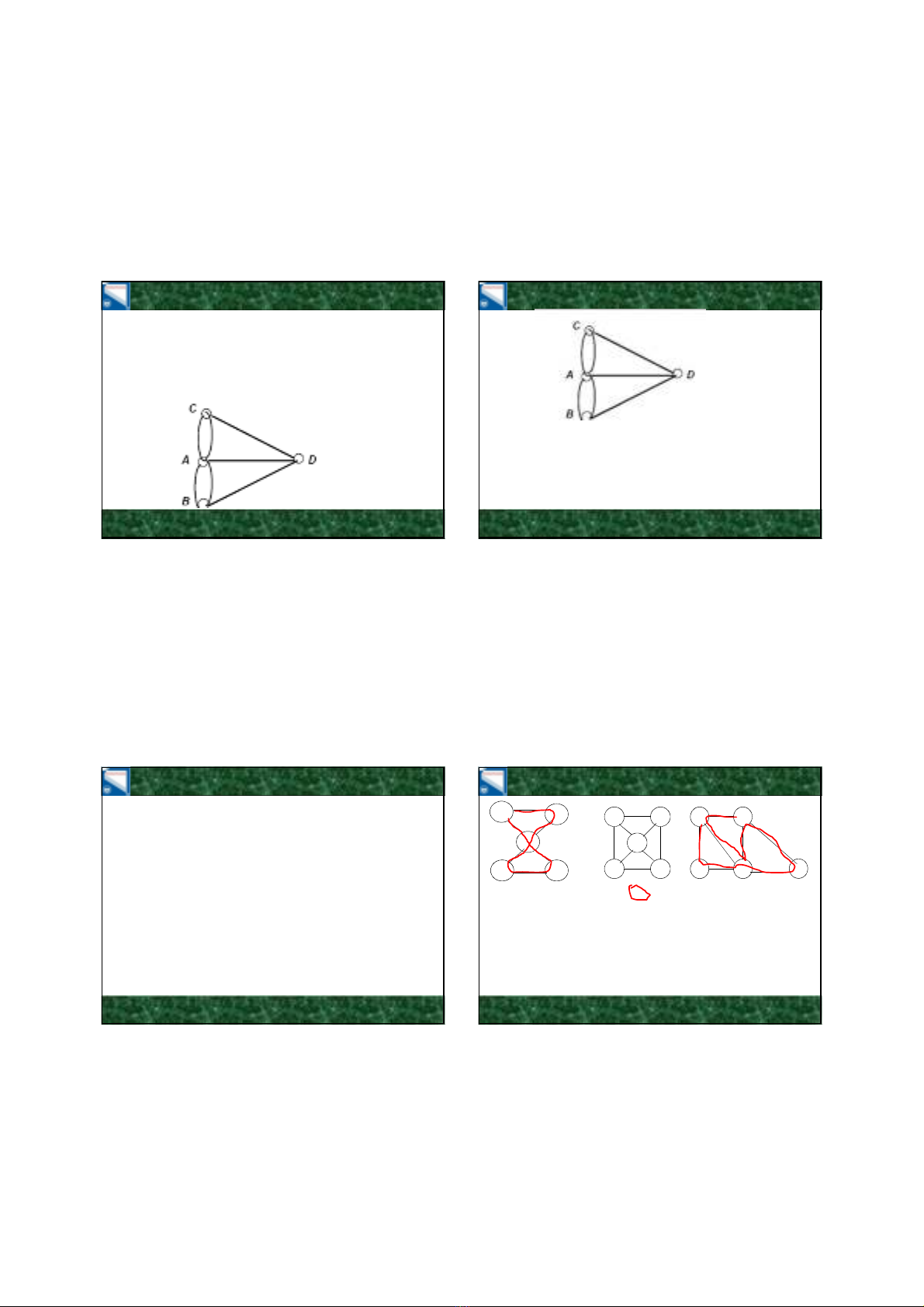
ĐƯỜNG ĐI & ĐỒ THỊ EULER
Đ th G1 làđ th Euler vìcóchu trình Euler:
a,e,c,d,e,b,a
Đ th G2 không cóchu trình cũng như đưng đi
Euler
Đ th G3 làđ th na Euler vìcóđưng đi Euler:
a,c,d,e,b,d,a,b
a b
d c
e
a b
c d e
G1 G2 G3
ab
d c
e

3
22 October 2012 9
ĐƯỜNG ĐI & ĐỒ THỊ EULER
b) Đnh lý1
i) Cho G=(V,E) làđ th vô hưng liên thông.
G làđ th Euler ⇔ Mi đnh ca G đu có
bc
chn.
ii) Nu G cóhai đnh bc l còn mi đnh khác
đu cóbc chn thìG cóđưng đi Euler.
22 October 2012 10
ĐƯỜNG ĐI & ĐỒ THỊ EULER
c) Thut toán Fleury đ tìm chu trình Euler
Btđu tmtđnh bt kỳca G vàtuân theo
qui tc sau:
–Mi khi đi qua mt cnh nào đóthìxoánóđi, sau
đóxoáđnh cô lp nu có.
–Không bao gi đi qua mt cu tr phi không còn
cách đi nào khác
22 October 2012 11
ĐƯỜNG ĐI & ĐỒ THỊ EULER
u sv w
t x y z
Víd: chu
trình Euler
uvwyswzyxtvx
u
Tu, theo (u,v) hoc (u,x), gis(u,v) (xoá(u,v)). Tv chn 1
trong: (v,w), (v,x), (v,t), gis(v,w) (xoá(v,w)). Theo 1 trong
3: (w,s), (w,y), (w,z), gis(w,s) (xoá(w,s)). Theo (s,y) (xoá
(s,y) vàs). Vì(y,x) làcu nên theo 1 trong 2: (y,w), (y,z), gis
(y,w) (xoá(y,w)). Theo (w,z) (xoá(w,z) & w) & theo (z,y) (xoá
(z,y) & z). Theo (y,x) (xoá(y,x) vày). Vì(x,u) làcu nên theo
(x,v) hoc (x,t), gis(x,v) (xoá(x,v)). Theo (v,t) (xoá(v,t) vàv),
theo (t,x) (xoá(t,x) vàt), theo (x,u) (xoá(x,u), x & u)
22 October 2012 12
BÀI TOÁN NGƯỜI PHÁT THƯ TRUNG HOA
Một nhân viên đi từSởBưuĐiện, qua một số
đường phố để phát thư, rồi quay vềSở. Ngườiấy
phảiđi qua các đường theo trình tựnào để đường
đi là ngắn nhất?
Bài toán được nhà toán học Trung Hoa Guan nêu
lên đầu tiên (1960), vì vậy thường được gọi là “bài
toán người phát thưTrung Hoa”.

4
22 October 2012 13
BÀI TOÁN NGƯỜI PHÁT THƯ TRUNG HOA
(tip) Bài toán quy vdng: Cho đ thliên
thông G. Mt hành trình ca ngưiđưa thưlà
mt chu trình qua mi cnh ca G, hãy tìm
hành trình ngn nht, tc làqua ít cnh nht.
Nu G làđ thEuler (miđnh đu cóbc
chn) thìchu trình Euler trong G (qua mi
cnh ca G đúng mt ln) làhành trình ngn
nht cn tìm.
Chcòn phi xét trưng h p G cómt s! đnh
bc l. Khi đó, mi hành trình trong G phiđi
qua ít nht hai ln mt s!cnh nàođó.
22 October 2012 14
BÀI TOÁN NGƯỜI PHÁT THƯ TRUNG HOA
(tip) D"thy r#ng mt hành trình qua mt cnh
(u,v) nàođóquáhai ln thìkhông phi làhành trình
ngn nht trong G. Vìvy, ta chcn xét nhng hành
trình T đi qua hai ln mt s!cnh nàođóca G
Ta quy ưc xem mi hành trình T trong G làmt
hành trình trong đ thEuler GT, cóđư c tG b#ng
cách v$thêm mt cnh song song đ!i vi nhng
cnh màTđi qua hai ln. Bài toánđt ra đư cđưa
vbài toán sau:
Trong cácđ thEuler GT, tìmđ thcós!cnh ít
nht (khi đóchu trình Euler trong đ thnày làhành
trình ngn nht).
22 October 2012 15
BÀI TOÁN NGƯỜI PHÁT THƯ TRUNG HOA
Đnh lý (Gooodman & Hedetniemi) Nu G làmt
đ thliên thông cóq cnh thìhành trình ngn nht
trong G cóchiu dài: q + m(G), m(G) làs!cnh mà
hành trình đi qua hai ln vàđư c xácđnh nhưsau:
–Gi V0(G) làtp h p cácđnh bc l(2k đnh) ca G. Ta
phân 2k phn tca G thành k cp, mi tp h p k cp gi
làmt phân hoch cp ca V0(G)
–Ta giđ dàiđưng đi ngn nht tuđn v làkhong
cách d(u,v). Đ!i vi mi phân hoch cp Pi, ta tính khong
cách gia hai đnh trong tng cp, ri tính t%ng d(Pi). S!
m(G) b#ng c&c tiu ca các d(Pi): m(G)=min d(Pi).
22 October 2012 16
BÀI TOÁN NGƯỜI PHÁT THƯ TRUNG HOA
Gii bài toán ngưi phát thưTrung Hoa cho đ th
sau: D
C E
BJ FK
H GIA

5
22 October 2012 17
BÀI TOÁN NGƯỜI PHÁT THƯ TRUNG HOA
Tp h p cácđnh bc lVO(G)={B, G, H, K} vàtp h p
các phân hoch cp làP={P1, P2, P3}, trong đó
P1={(B, G), (H, K)}→d(P1) = d(B, G)+d(H, K) =4+1
=5,
P2={(B, H), (G, K)}→d(P2)= d(B, H)+d(G, K)=2+1=
3,
P3={(B, K), (G, H)}→d(P3) = d(B, K)+d(G, H) =
3+2=5.
m(G) = min(d(P1), d(P2), d(P3)) = 3
Do đóGTcóđư c tG b#ng cách thêm vào3cnh:
(B, I), (I, H), (G, K) vàGTlàđ thEuler. Vy hành
trình ngn nht cn tìm làđi theo chu trình Euler
trong GT:
A, B, C, D, E, F, K, G, K, E, C, J, K, H, J, I, H, I, B, I, A 22 October 2012 18
BÀI TOÁN NGƯỜI PHÁT THƯ TRUNG HOA
A, B, C, D, E, F, K, G, K, E, C, J, K, H, J, I, H, I, B, I, A
D
C E
FB KJ
A I H G
22 October 2012 19
ĐƯỜNG ĐI & ĐỒ THỊ HAMILTON
Năm 1857, nhà toán hc ngưi Ailen là Hamilton
(1805-1865) đưa ra trò chơi “đi vòng quanh th
gii” nhưsau:
Cho mt hình thp nhdi)nđu (đa di)nđu có
12 mt, 20 đnh và 30 cnh), miđnh ca hình
mang tên mt thành ph!n%i ting, mi cnh ca
hình (n!i hai đnh) là đưng đi li gia hai thành
ph!tương ng. Xut phát tmt thành ph!, hãy
tìm đưng đi thăm tt ccác thành ph!khác, mi
thành ph!chmt ln, ri tr*vchcũ.
22 October 2012 20
ĐƯỜNG ĐI & ĐỒ THỊ HAMILTON
a) ĐN
Đưng đi Hamilton là đưng đi qua tt ccác
đnh cađ thmiđnh đúng mt ln.
Chu trình btđu tmtđnh vnào đó và đi qua
tt ccác đnh còn li, miđnh đúng mt ln gi
là chu trình Hamilton (mch Hamilton)
Đ thgi là đ thHamilton nu nó có chu trình
Hamilton, gi là na Hamilton nu nó có đưng
đi Hamilton
















![Ngân hàng câu hỏi môn Toán rời rạc [mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2026/20260222/dangminhquangfpc@gmail.com/135x160/49231771810501.jpg)









