
TRƯỜNG ĐẠI HỌC BÁCH KHOA TP.HCM
--oOo--
BÁO CÁO BÀI TẬP LỚN MÔN
PHƯƠNG PHÁP TÍNH
Họ và tên: Nguyễn Duy Khang
MSSV: 2113665
Nhóm: 11
Lớp: L05
Mã số M (các câu 1,2,3,4): 2.9908
TP HỒ CHÍ MINH

Câu 5 :
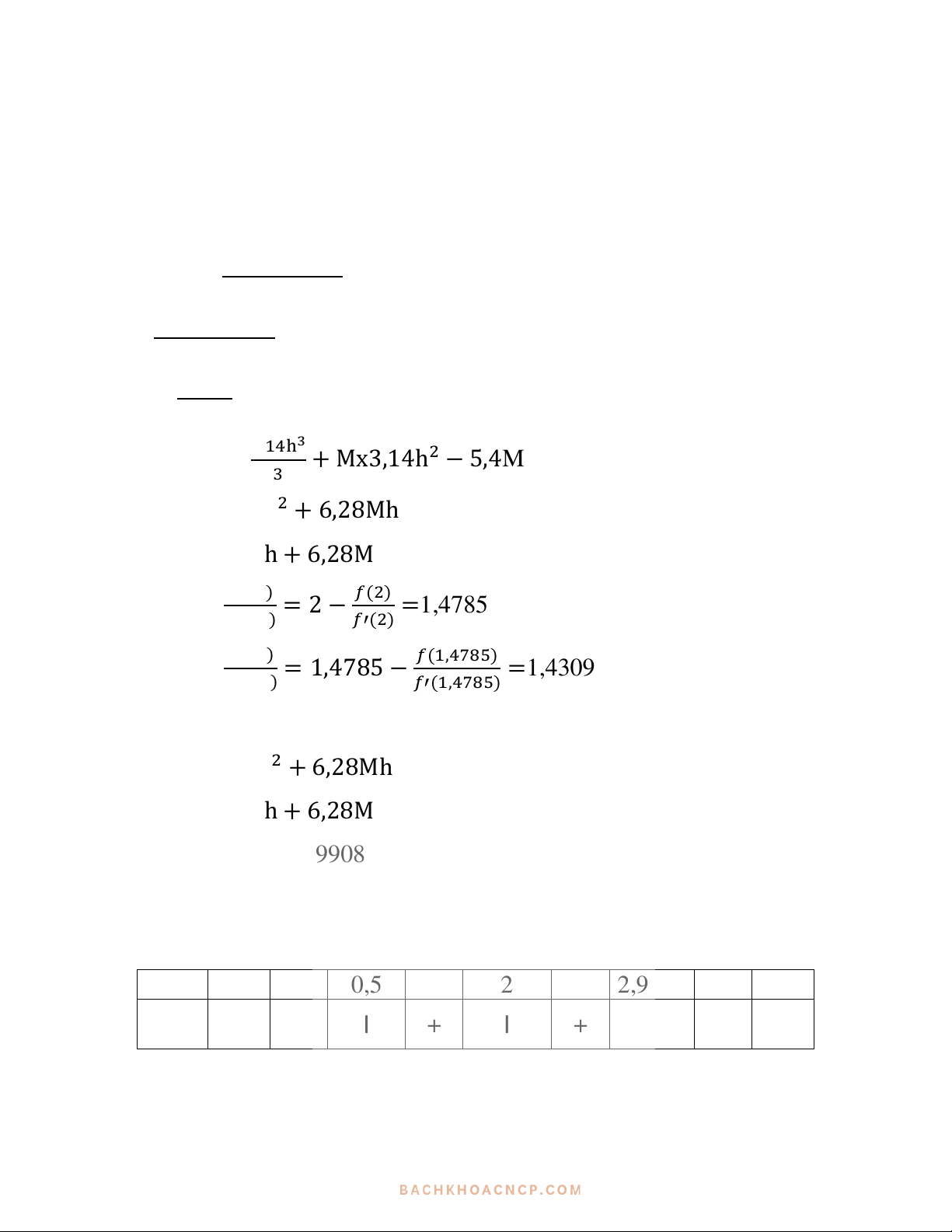
Giải : với M=2,9908
I/Phần bài tập cá nhân:
Câu 1:
Ta có:V=3,14h2(3M−h)
3=5,4M
<=>3,14h2(3M−h)
3−5,4M=0
<=>−3,14h3
3+Mx3,14h2−5,4M=0
Đặt f(h)=−3,14h3
3+Mx3,14h2−5,4M
f′(h)=−3,14h2+6,28Mh
f′′(h)=−6,28h+6,28M
ℎ1=ℎ0−𝑓(ℎ0)
𝑓′(ℎ0)=2−𝑓(2)
𝑓′(2)=1,4785
ℎ2=ℎ1−𝑓(ℎ1)
𝑓′(ℎ1)=1,4785−𝑓(1,4785)
𝑓′(1,4785)=1,4309
*Tính Sai Số ℎ2
f′(h)=−3,14h2+6,28Mh
f′′(h)=−6,28h+6,28M
f’’(h)=0<=>h=M=2,9908
Bảng biến thiên:
h
-∞
0,5
2
2,9908
+∞
f’’(h)
+
I
+
I
+
0
-

Khi h є [0,5;2,0] thì f’(h) đồng biến nên giá trị nhỏ nhất của f’(h) є
[0,5;2,0] là f’(0,5)= 8,6061 mà f’(h) luôn dương trên [0,5;2,0]
𝑚−
<|𝑓′(ℎ)|=8,6061
Ta có : |ℎ2−ℎ∗|−
<|𝑓(ℎ2)|
𝑚=0,0014
Matlab
Code
%nhap ham f, f' vao cmd va chay newtonss(f,fd)
%f = @(x)((3.14*x^2*(3*M-x))/3)-5.4*M;
%fd = @(x)3.14*2*x*M-3.14*x^2;
%newtonss(f,fd)
%nhap h0
%nhap h min
function [x,ss] = newtonss(f,fd)
eps = 1.0E-6; N=3;
x0 = input('nhap x0 ');
x = x0;
xm = input('nhap xm ');
m = fd(xm);
n = 1; err = eps+1
while (n < N && err > eps)
x1 = x - f(x)/fd(x);
err = abs(f(x1))/m;
n=n+1; x=x1
ss = f(x)/m;
double(ss)
disp('so lan lap la '),disp(n-1);
disp('gia tri x* la : '),disp(x);
disp('sai so x* '),disp(ss);
end
end
Kết quả
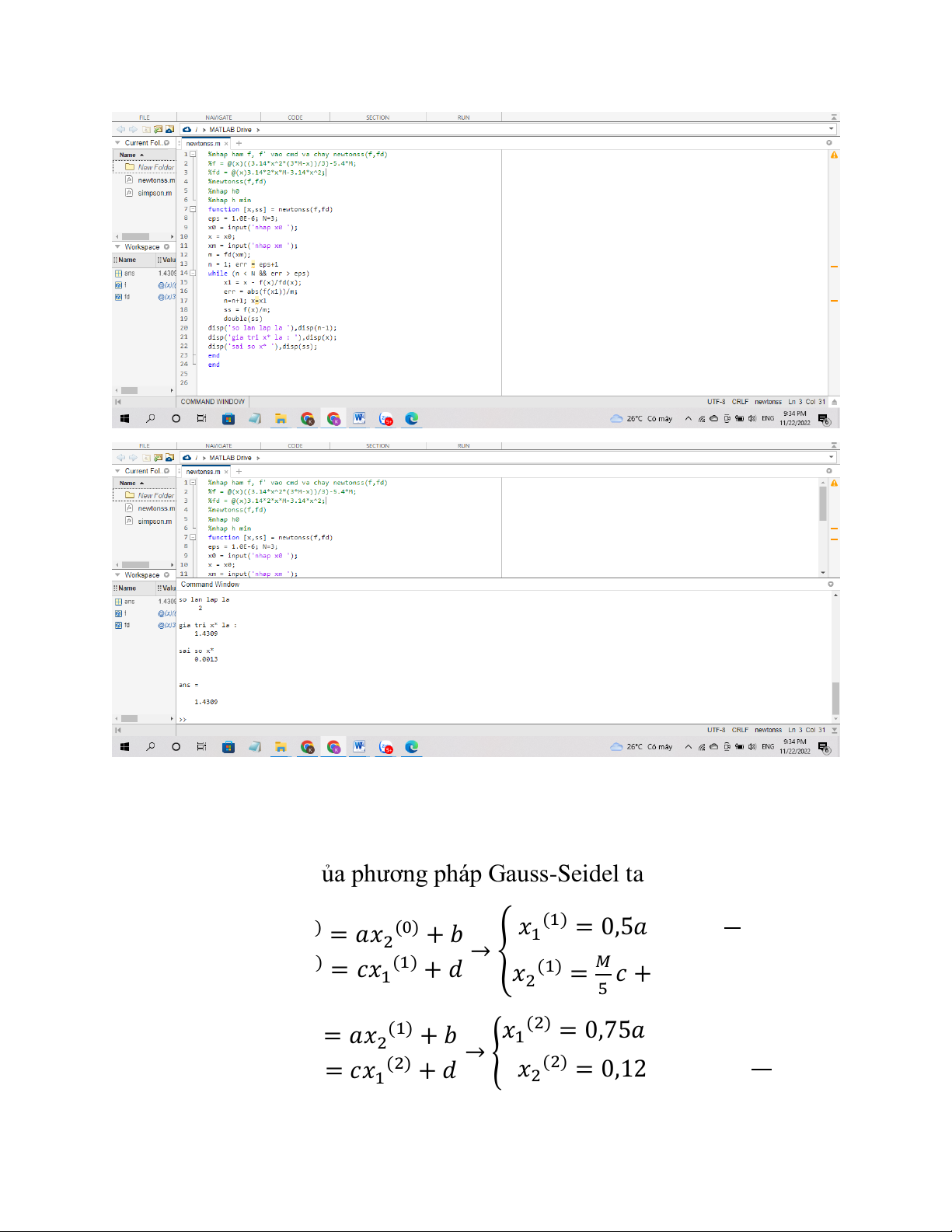
Câu 2:
Theo công thức lặp của phương pháp Gauss-Seidel ta có :
Khi k=0,ta có {𝑥1(1)=𝑎𝑥2(0)+𝑏
𝑥2(1)=𝑐𝑥1(1)+𝑑 →{𝑥1(1)=0,5𝑎+𝑏=𝑀
5
𝑥2(1)=𝑀
5𝑐+𝑑=0,75
Khi k=1,ta có {𝑥1(2)=𝑎𝑥2(1)+𝑏
𝑥2(2)=𝑐𝑥1(2)+𝑑→{𝑥1(2)=0,75𝑎+𝑏=0,125
𝑥2(2)=0,125𝑐+𝑑=𝑀
10


























