Trường Đại học Công nghiệp thành phố Hồ Chí Minh
Khoa Công nghệ Cơ khí
CHƯƠNG 06:
TỐI ƯU HÀM NHIỀU BIẾN SỐ
VỚI RÀNG BUỘC TỔNG QUÁT:
PHƯƠNG PHÁP CỔ ĐIỂN
Thời lượng: 3 tiết
2
Tối ưu hàm nhiều biến với ràng buộc tổng quát
fx
Tìm cực trị (Optimum) của hàm nhiều biến sau:
Với m điều kiện ràng buộc bất đẳng thức:
Với:
12
T
n
x x xx
0
1, 2, ,
j
g
jm
x
Với p điều kiện ràng buộc đẳng thức:
0
1, 2, ,
l
h
lp
x
3
Điều kiện Karush-Kuhn-Tucker
11
1 2 1 2 1 2
,,
;;
p
m
j j l l
jl
T
TT
n m p
L f g h
x x x





xλ η x x x
xλη
11
, , 0; 1.. 1
0; 1.. 2
0; 1.. 3
0 min
; 1.. 4
0 max
0; 1.. 5
p
m
jl
jj
jl
i i i i
jj
j
j
j
l
gh
Lf in
x x x x
g j m
g j m
fjm
f
h l p







xλ η x x x
x
x
x
x
x
4
Điều kiện Karush-Kuhn-Tucker (Tiếp)
1
11
2
22
;;
p
nm
x
x
x










xλη
Giải hệ
(1)÷(5) với
(n+m+p) ẩn,
ta có:
Kiểm tra J1 véctơ Gradient của hàm bất đẳng thức ràng buộc g
tại điểm cực trị và p véc tơ Gradient của hàm đẳng thức ràng
buộc h tại điểm cực trị x*, phải là không phụ thuộc tuyến tính
với nhau. Nếu vậy thì x*, λ*, η* sẽ là điểm cực trị.
10
j
j
g
jJ

x
và KHÔNG PHỤ THUỘC TUYẾN TÍNH
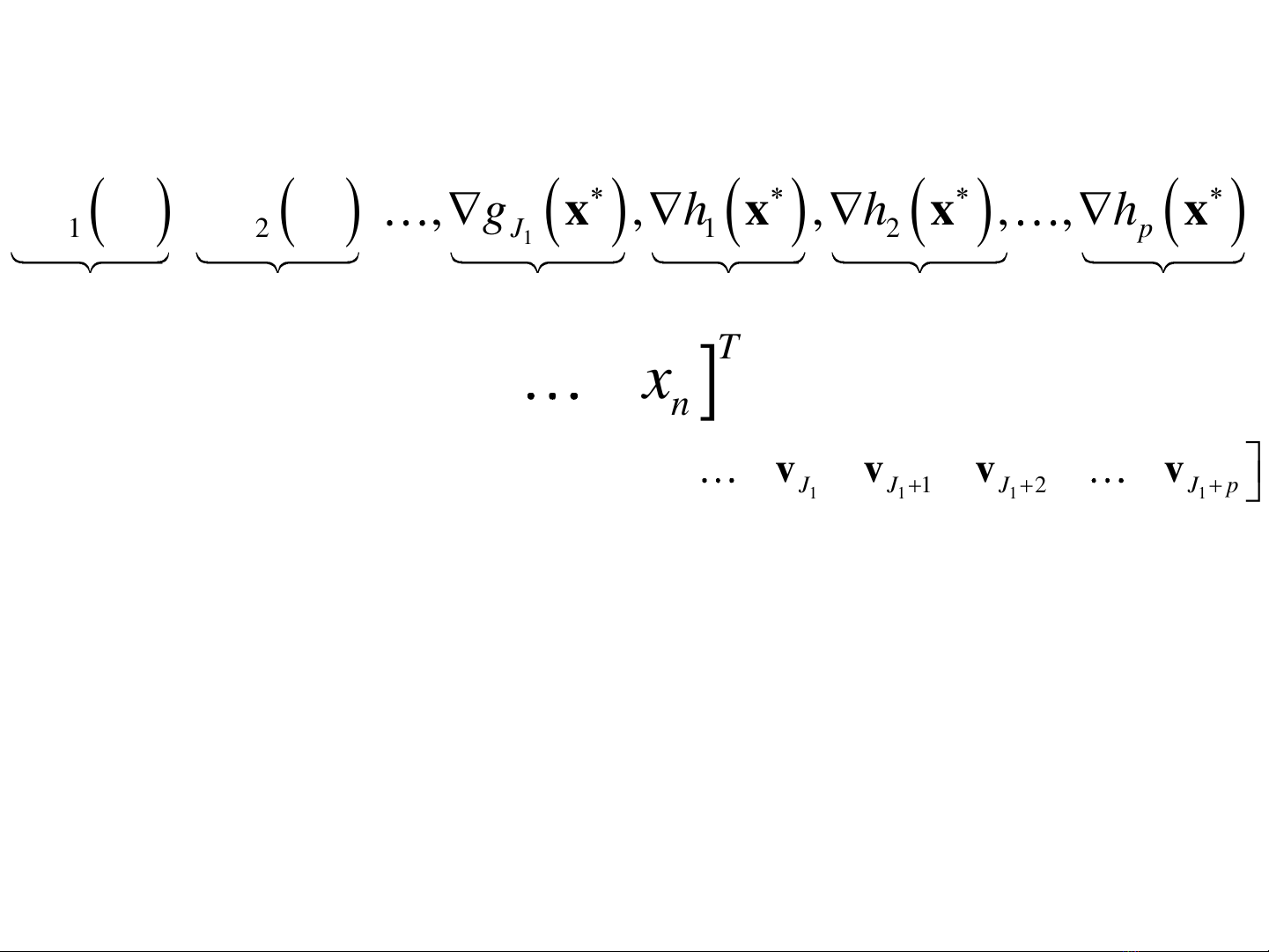
Không phụ thuộc/phụ thuộc tuyến tính 5
Cho M = J1+p véc tơ:
1
1 2 1 2
1 1 1 1
1 2 1 2
, , , , , , ,
p
J J J J
Jp
g g g h h h
v v v v v v
x x x x x x
Với:
12
T
n
x x xx
Xây dựng ma trận A:
1 1 1 1
1 2 1 2
x M
1;
J J J J p
N
M J p N n
A v v v v v v
Trường hợp 1: Khi M > N Các véc tơ sẽ luôn phụ thuộc tuyến tính
Trường hợp 2: Khi M = N Ta tính det(A). Nếu det(A) = 0 thì phụ thuộc
tuyến tính, ngược lại thì không phụ thuộc tuyến tính.
Trường hợp 3: Khi M < N, Ta tính rank(A). Nếu rank(A)=M tức là bằng
số lượng véc tơ thì hệ độc lập tuyến tính. Nếu khác rank(A)≠M thì hệ
phụ thuộc tuyến tính.