PHẠM Đỗ Chung-HNUE-2019
VẬT$LÍ$CHẤT$RẮN
Phạm%Đỗ%Chung
Bộ#môn#Vật#lí#chất#rắn#–Điện#tử
Khoa#Vật#lí,#ĐH#Sư#Phạm#Hà#Nội
136#Xuân#Thủy,#Cầu#Giấy,#Hà#Nội
Lớp%Y20%–Sư%phạm%Vật%lí
PHẠM Đỗ Chung-HNUE-2019
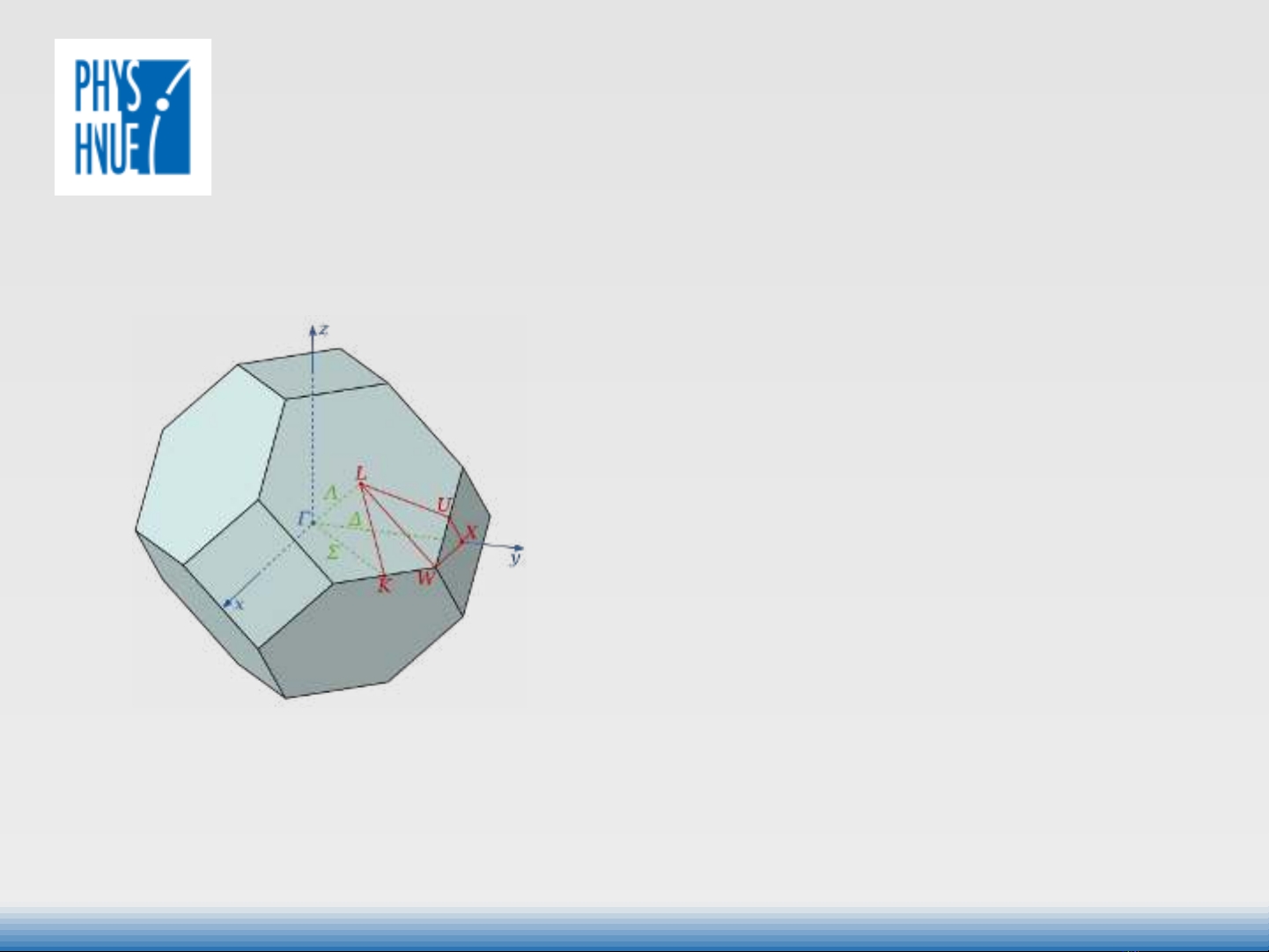
Chương$4
Lí$thuyết$dải$năng$lượng
1. Electron trong trường thế tuần hoàn của tinh%thể
2. Mô hình electron liên kết yếu (định tính)
3. Mô hình electron liên kết mạnh (định tính)
4. Kim loại,bán dẫn và điện môi
5. Hàm Bloch
6. Mô hình electron liên kết yếu (định lượng)
7. Mô hình electron liên kết mạnh (định lượng)
8. Phương trình chuyển động của electron và lỗ
trống
2
PHẠM Đỗ Chung-HNUE-2018 3
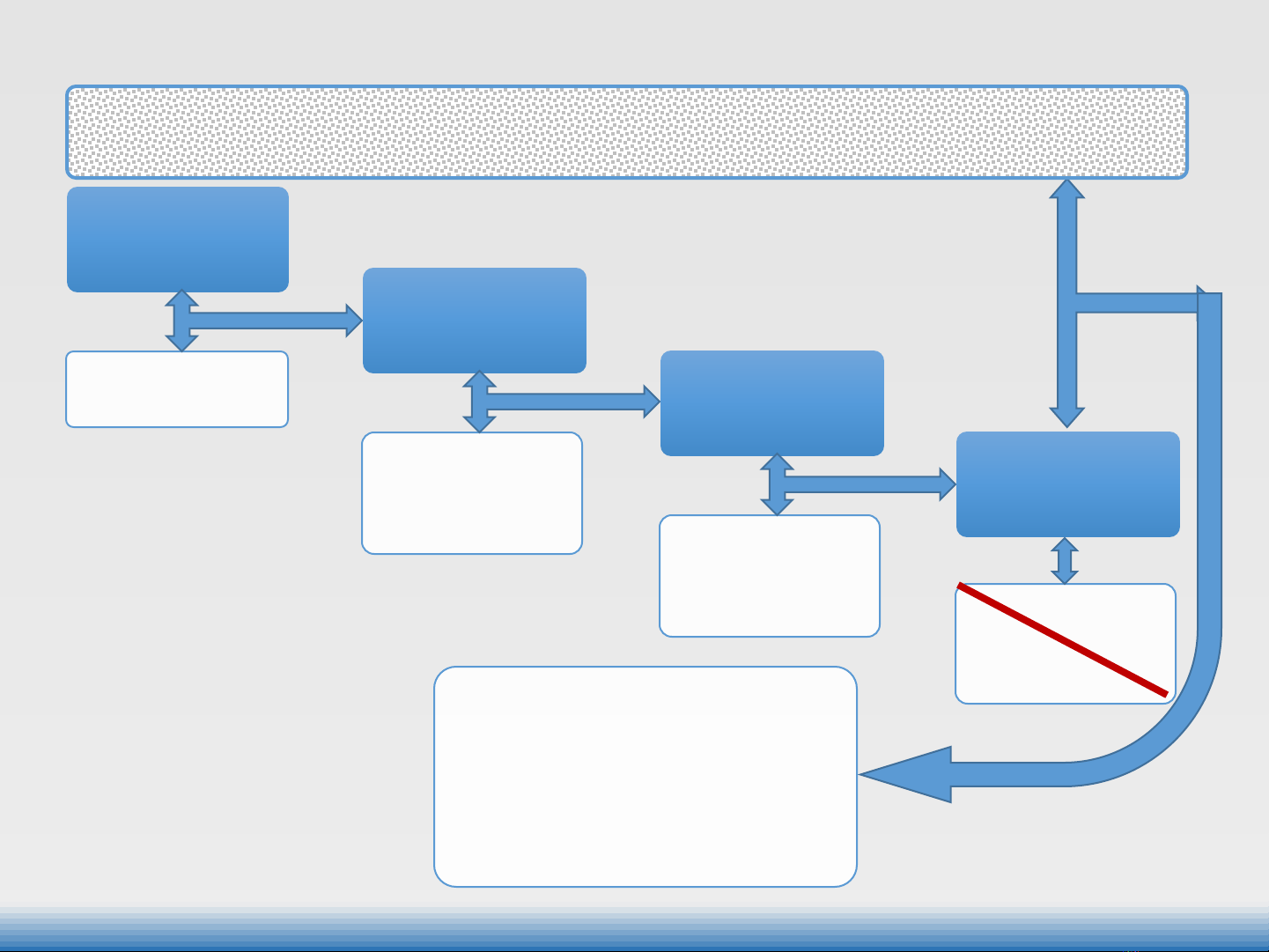
Mạng%không%
gian
Gốc
Mạng%tinh%
thể
Gốc%hình%
cầu%cứng
Các%cấu%trúc%
xếp%chặt
Gốc%tương%tác%
lẫn%nhau
Các%loại%tinh%
thể%(ion,…)
Gốc%
dao%động
Dải%năng%lượng
Electron
PHẠM Đỗ Chung-HNUE-2018
5.$Hàm$Bloch
Phương trình Schrödinger qui định hàm sóng
(trạng thái) của electron
4
)r(E)r()r(V
m2
2
2!!!
"ψ=ψ
⎥
⎦
⎤
⎢
⎣
⎡+∇
−
Nếu trường thế tuần hoàn 𝑉 𝑟#+𝑅 = 𝑉 𝑟# ,thì
hàm riêng của phương trình sóng là hàm Bloch:
𝜓(𝑟# =𝑢(𝑟# 𝑒+(,
#
ởđó:𝑢(𝑟# =𝑢(𝑟# +𝑅 (tuần hoàn theo chu kỳ
mạng tinh thể)
PHẠM Đỗ Chung-HNUE-2018
5.$Hàm$Bloch
Chứng minh:định lí Bloch cho mạng 1chiều (dài
L=Na) với điều kiện hàm sóng không suy biến:
5
Thế tuần hoàn (chu kỳ a):𝑈 𝑥 +𝑠.𝑎 =𝑈 𝑥
𝜓2x+𝑎 = 𝐶𝜓2x
Từ điều kiện tuần hoàn tịnh tiến của hàm sóng
Áp dụng điều kiện biên tuần hoàn
𝜓2x+𝑁𝑎 = 𝜓2x =𝐶6𝜓2x
C = 𝑒+89:/6;2s =0,%1,%…, N-1
𝜓2x =𝑢((x)𝑒+89:@/6A