Tuyển tập Hội nghị Khoa học thường niên năm 2024. ISBN: 978-604-82-8175-5
312
HÀM PHỔ CỦA MÔ HÌNH HUBBARD ION
MẠNG TỔ ONG HAI CHIỀU TƯƠNG TỰ SILICENE
Nguyễn Thị Hương
Trường Đại học Thủy lợi, email: nthuong@tlu.edu.vn
1. GIỚI THIỆU CHUNG
Silicene là một lớp đơn nguyên tử silic có
cấu trúc mạng tổ ong hai chiều hiện đang
được nghiên cứu rộng rãi vì những ứng dụng
thiết thực của nó trong khoa học và công
nghệ [1]. Tuy nhiên, hiện nay việc chế tạo
silicene tồn tại độc lập vẫn chưa thực hiện
được. Gần đây, silicene đã được tổng hợp
thành công bằng cách lắng đọng silic trên
mặt phẳng bạc (Ag) [2]. Lý do bạc được
chọn là chất nền lý tưởng để nuôi silicene vì
xu hướng để tạo thành một hợp kim Ag - Si
là thấp. Tính chất điện tử của silicene phụ
thuộc như thế nào vào chất nền hiện đang
thu hút được sự quan tâm của rất nhiều nhà
khoa học.
Mô hình Hubbard (HM) đã được sử dụng
để nghiên cứu hệ điện tử tương quan trên
mạng tổ ong hai chiều tương tự graphene [3].
Mô hình Hubbard ion (HIM) có thể coi là mở
rộng của HM khi xét đến thế ion mô tả tương
tác của mạng tinh thể với chất nền [4]. Bài
báo cáo sẽ nghiên cứu hàm phổ của IHM
mạng tổ ong hai chiều để từ đó là cơ sở đánh
giá tính chất điện tử của hệ.
Do tương tác phức tạp của hệ nhiều hạt
nên bài báo cáo áp dụng gần đúng thế kết hợp
(CPA) cho IHM để nghiên cứu hàm phổ.
CPA là một phương pháp gần đúng thay thế
trường ngẫu nhiên bằng một trường hiệu
dụng đồng nhất thỏa mãn yêu cầu tự hợp.
CPA đã được áp dụng để nghiên cứu hệ điện
tử tương quan trong HM.
2. PHƯƠNG PHÁP NGHIÊN CỨU
Silicene có cấu trúc lục giác, được cấu
thành bởi hai mạng con tam giác lồng vào
nhau do có hai nguyên tử trên một ô cơ sở.
Vector cơ sở của mạng thuận là:

13, 3 ,
2
a
a

23, 3
2
a
a
.
Vector cơ sở của mạng đảo là:

1
21, 3 ,
3
ba

2
21, 3
3
ba

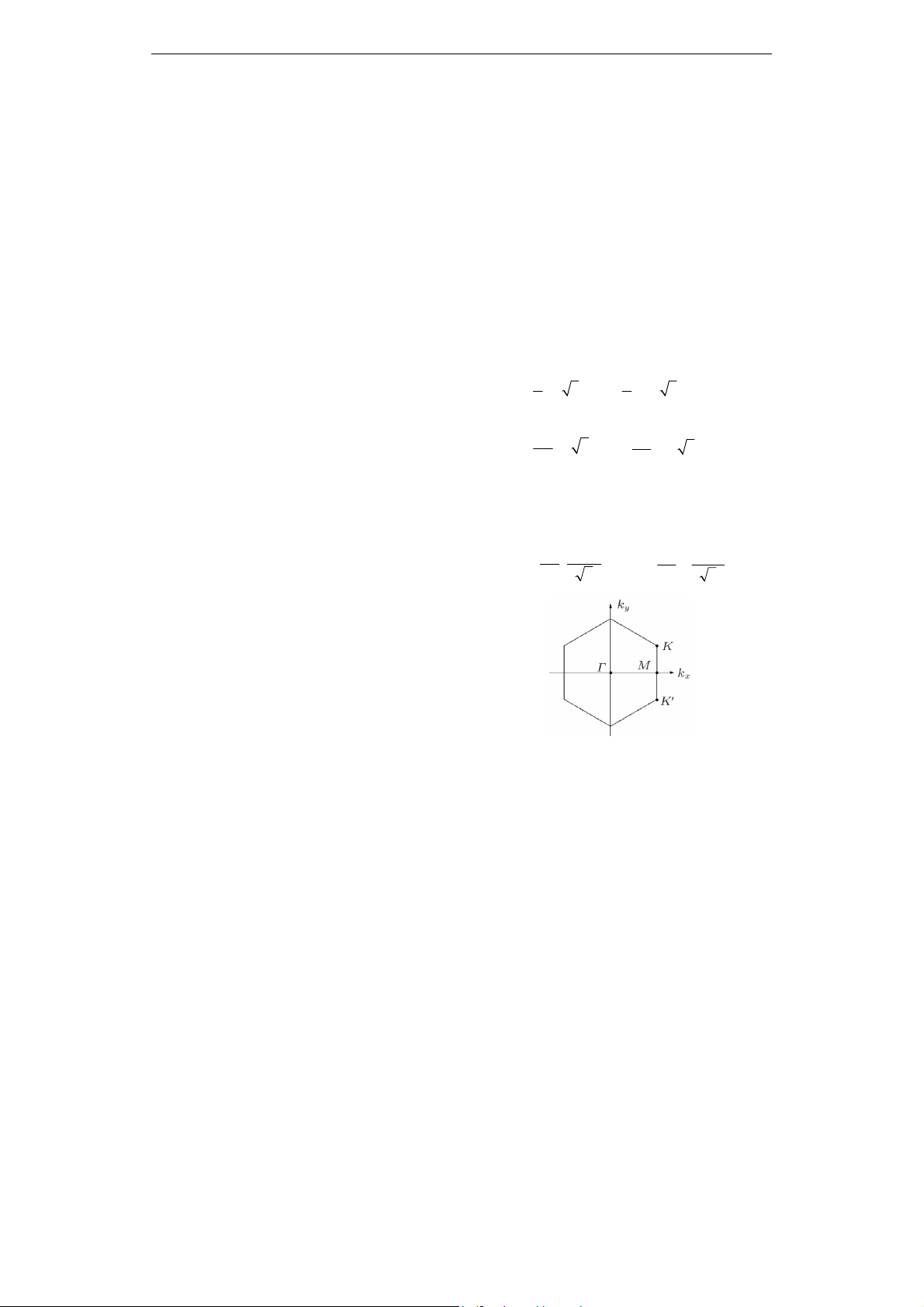
Từ đó ta xác định được vùng Brillouin thứ
nhất (FBZ) của mạng tổ ong hai chiều (Hình
1). K và K’ tại các đỉnh của vùng Brillouin
thứ nhất có tọa độ:
a
a
K33
2
,
3
2
,
a
a
K33
2
,
3
2
'
.
Hình 1. FBZ của mạng tổ ong hai chiều
Hamiltonian của IHM trên một mạng tổ
ong hai chiều tương tự silicene có dạng:
,,
..
,
ij ii
iAjB i
ij
AiBi i
iA iB i
Ht ccHcUnn
nnn










 (1)
trong đó: t là tham số nhảy nút được lấy giới
hạn cho các vị trí lân cận gần nhất, U là
tương tác Coulomb được lấy giới hạn trên
một nút,
A = và
B =  là các năng lượng
Tuyển tập Hội nghị Khoa học thường niên năm 2024. ISBN: 978-604-82-8175-5
313
ion hóa, thế hóa học được chọn là
= U/2
cho trạng thái lấp đầy một nửa.
Trong gần đúng tương tự hợp kim (AAA),
xét điện tử có spin hướng lên chuyển động
trong trường thế tạo bởi các điện tử có spin
hướng xuống đóng băng trên mạng tinh thể,
Hamiltonian (1) có dạng
,,,
,
.. ,
AAA i j A i B i
iAjB iA iB
ij
H
tccHc En En








(2)
trong đó: EU

Ở đây α = A, B.
Gần đúng CPA thay trường thế ngẫu nhiên
E

bằng một trường thế đồng nhất ()

(năng lượng riêng). Khi đó, Hamiltonian của
IHM trong gần đúng CPA:
,,
,
,
.
CPA
iAjB
ij
AB
j
i
ii
iB
iA
HtccHc
nn








(3)
Hàm Green địa phương tìm được từ
phương trình chuyển động của hàm Green:
 
2
1,
k
Ft


 



(4)
ở đây α = A(B),
= B(A). Phép tính tổng
được thực hiện trong vùng Brillouin thứ nhất:
2 2 23 43
,
339 9
xy
kk





Hàm Green trung bình được xác định
thông qua phương trình Dyson.
 


,
,
()
1() 2
()1
1() 2
Fn
GU
F
Fn
U
F


 

 










(5)
Điều kiện tự hợp của CPA đòi hỏi hàm
Green trung bình phải trùng với hàm Green
địa phương:
() ()GF
 
(6)
Năng lượng riêng ()

và hàm Green
()G

được xác định bằng phương pháp tính
số. Bắt đầu bằng việc chọn một giá trị của
()

, ta xác định được hàm Green địa
phương (4). Thay giá trị này vào phương
trình (5) ta có hàm Green trung bình. Tiếp
theo, năng lượng riêng mới được xác định
theo công thức:
11
() () () ()FG
 


 (7)
Ta chạy vòng lặp (7) cho tới khi hội tụ với
tham số hội tụ lấy nhỏ hơn 10-3. Sau khi tìm
được hàm Green, ta xác định được hàm phổ
theo công thức:
() 2Im ()
a
AG

(8)
3. KẾT QUẢ NGHIÊN CỨU VÀ THẢO LUẬN
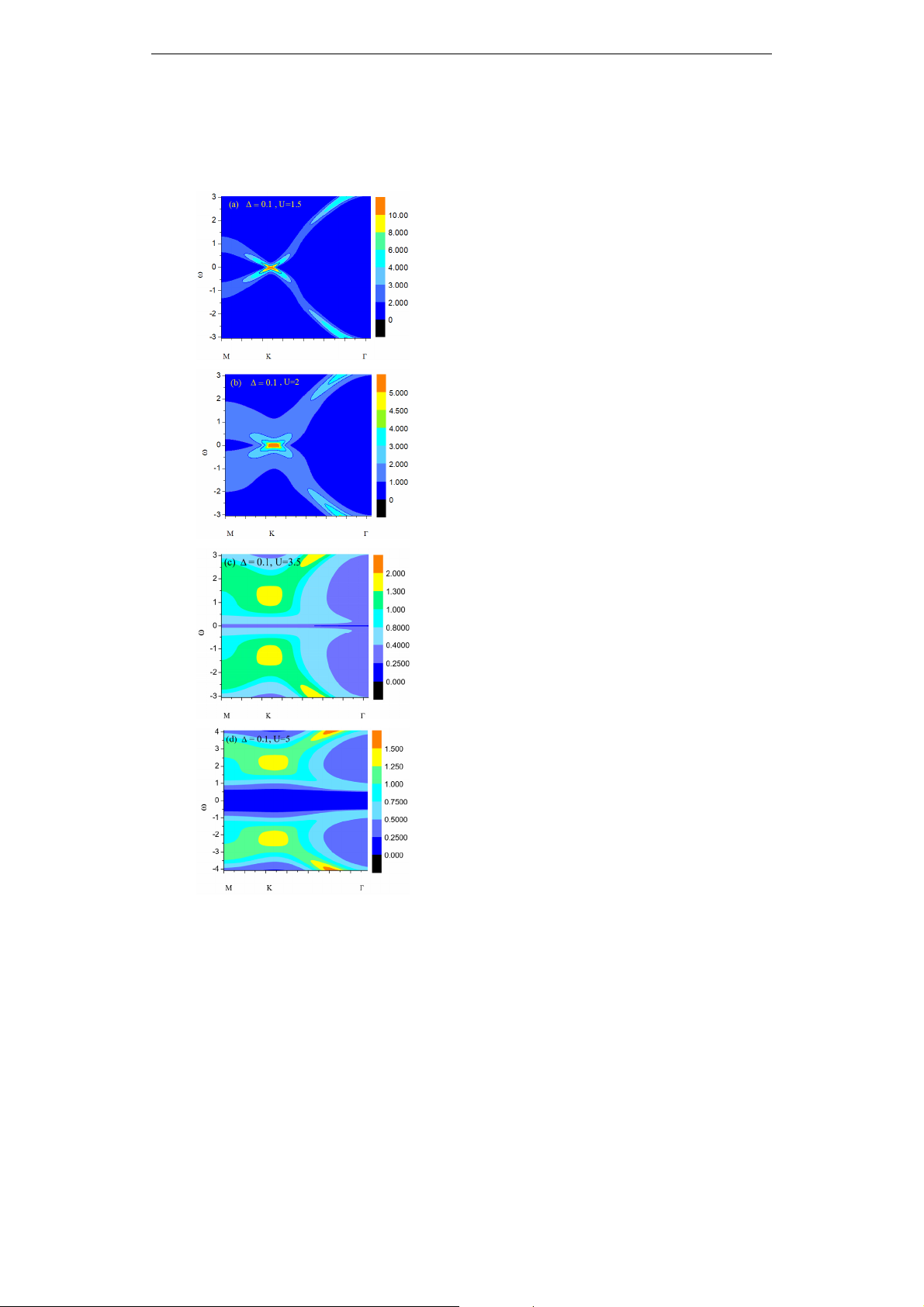
Hình 2. Hàm phổ dọc theo hướng M - K -
trong trường hợp không xét đến tương tác
Coulomb U
Hàm phổ trong bài báo cáo được biểu diễn
dọc theo hướng M - K -
. Tính chất điện tử
của hệ có thể quan sát thông qua hàm phổ
gần điểm Dirac K. Trường hợp không xét đến
tương tác Coulomb (U = 0) (Hình 2), nếu
không xét đến tương tác của mạng tinh thể
với chất nền (Hình 2a), hàm phổ tại điểm
Dirac K không tồn tại khe năng lượng và
hàm phổ phụ thuộc tuyến tính vào vector
sóng k
tại điểm Dirac K. Do đó, khi không
xét đến tương tác với nền và tương tác
với xác suất 1
n
,
với xác suất n
,
Tuyển tập Hội nghị Khoa học thường niên năm 2024. ISBN: 978-604-82-8175-5
314
Coulomb U, hệ ở pha bán kim. Tuy nhiên,
khi xét đến tương tác với nền (Hình 2b), tồn
tại khe năng lượng tại gần điểm Dirac K. Lúc
này hệ ở pha điện môi và tương tác với nền
là nguyên nhân đưa hệ từ pha bán kim sang
pha điện môi.
Hình 3. Hàm phổ dọc theo hướng M - K -
với
= 0.1 tại các giá trị khác nhau
của tương tác Coulomb U
Tuy nhiên khi tăng tương tác Coulomb U
thì khe năng lượng tại điểm Dirac K thu hẹp
dần và biến mất. Tương tác Coulomb đưa hệ
từ pha điện môi sang pha kim loại (Hình 3a,
3b). Khi tương tác Coulomb đủ lớn khe năng
lượng mở ra thêm một lần nữa và hệ xảy ra
quá trình chuyển pha lần thứ hai từ pha kim
loại sang pha điện môi (Hình 3c, 3d). Ở pha
điện môi thứ hai tương tác giữa các điện tử
lớn ngăn cản sự chiếm đóng đôi của các điện
tử trên một nút. Do đó pha điện môi thứ hai
là điện môi Mott được hình thành do tương
quan mạnh giữa các điện tử.
4. KẾT LUẬN
Bài báo cáo đã nghiên cứu ảnh hưởng
tương tác Coulomb và tương tác với chất nền
đến tính chất điện tử trong mô hình Hubbard
ion tương tự vật liệu silicene. Kết quả nghiên
cứu cho thấy trong trường hợp không xét đến
tương tác của các điện tử, tương tác với nền
là nguyên nhân đưa hệ từ pha bán kim sang
pha điện môi. Và với một giá trị của tương
tác với nền, tương quan điện tử đưa hệ từ pha
điện môi sang pha kim loại và sau đó sang
pha điện môi Mott. Các kết quả nghiên cứu lí
thuyết này sẽ là thông tin tham khảo cho các
nghiên cứu thực nghiệm trên silicene.
5. TÀI LIỆU THAM KHẢO
[1] Mubashir A. Kharadi, et al (2020), Review-
Silicene: From Material to Device
Applications, ECS Journal of Solid State
Science and Technology, 9, 115031.
[2] Junki Sone et al (2014), Epitaxial growth
of silicene on ultra-thin Ag(111) films, New
Journal of Physics Vol.16, 095004.
[3] Duc Anh Le (2013), Mott Transition In
The Half-filled Hubbard Model On The
Honeycomb Lattice Within Coherent
Potential Approximation, Mod. Phys. Lett.
B, Vol.27, 1350046.
[4] D. A. Rowlands and Zhang Yu-Zhong
(2014), Disappearance of the Dirac cone in
silicene due to the presence of an electric
field, Chin. Phys. B Vol. 23, 037101.