BÀI GI NG Ả
V K THU TẼ Ỹ Ậ
Thoát
Ph n th nh t ầ ứ ấ
C S Đ XÂY D NG B N VƠ Ở Ể Ự Ả Ẽ
Ch ng 1: TIÊU CHU N V TRÌNH BÀY B N Vươ Ẩ Ề Ả Ẽ
Ch ng 2: V HÌNH H Cươ Ẽ Ọ
Ch ng 3: KHÁI NI M V CÁC PHÉP CHI Uươ Ệ Ề Ế
Ch ng 3 ươ
HÌNH CHI U VUÔNG GÓCẾ
I. Khái ni m v các phép chi uệ ề ế
II. Hình chi u vuông góc c a 1 đi m, đng th ng, m t ế ủ ể ườ ẳ ặ
ph ngẳ
III. Hình chi u c a kh i hình h c đn gi nế ủ ố ọ ơ ả
IV. Cách v hình chi u c a v t thẽ ế ủ ậ ể
1. Phép chi u xuyên tâmế
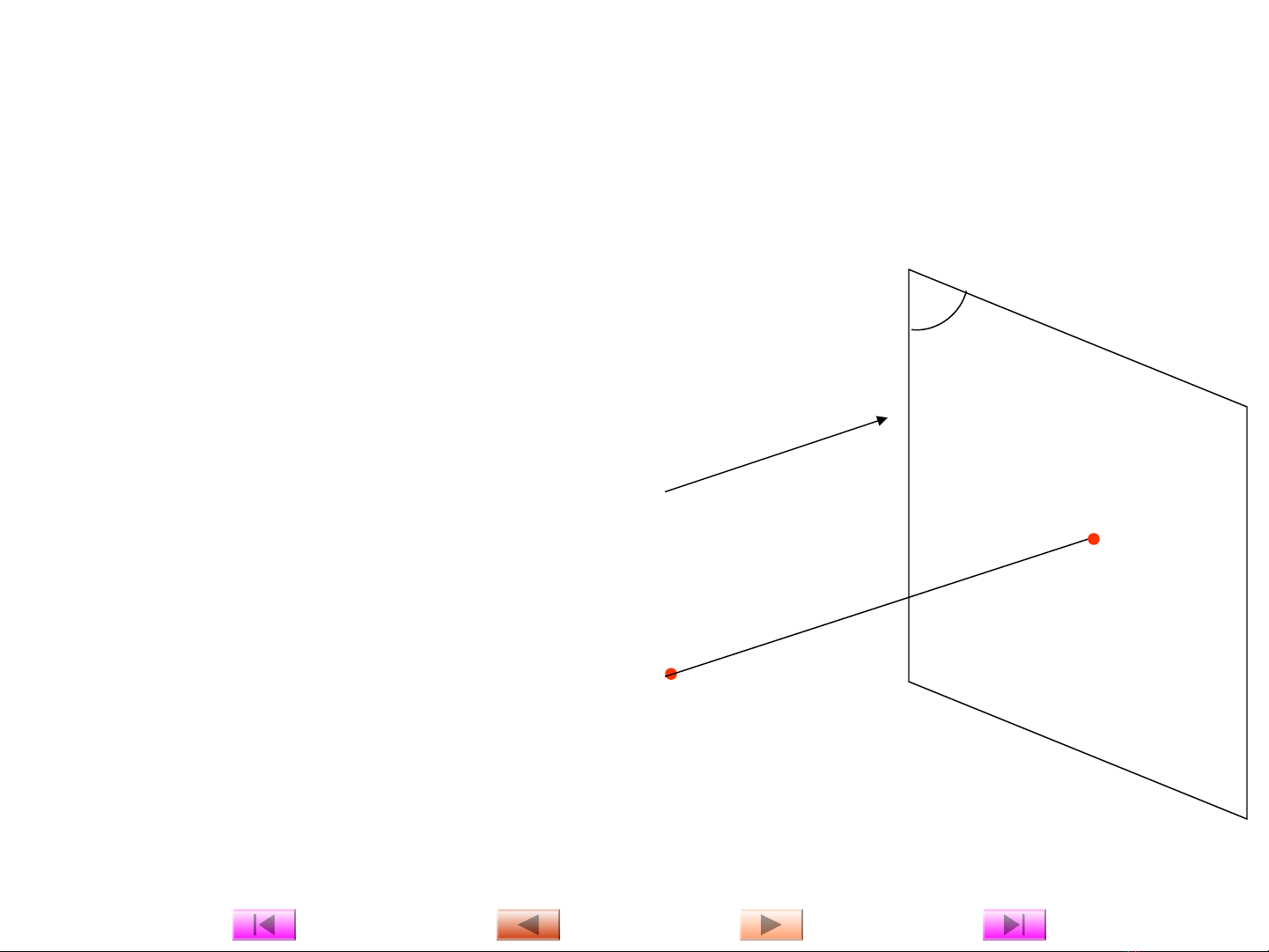
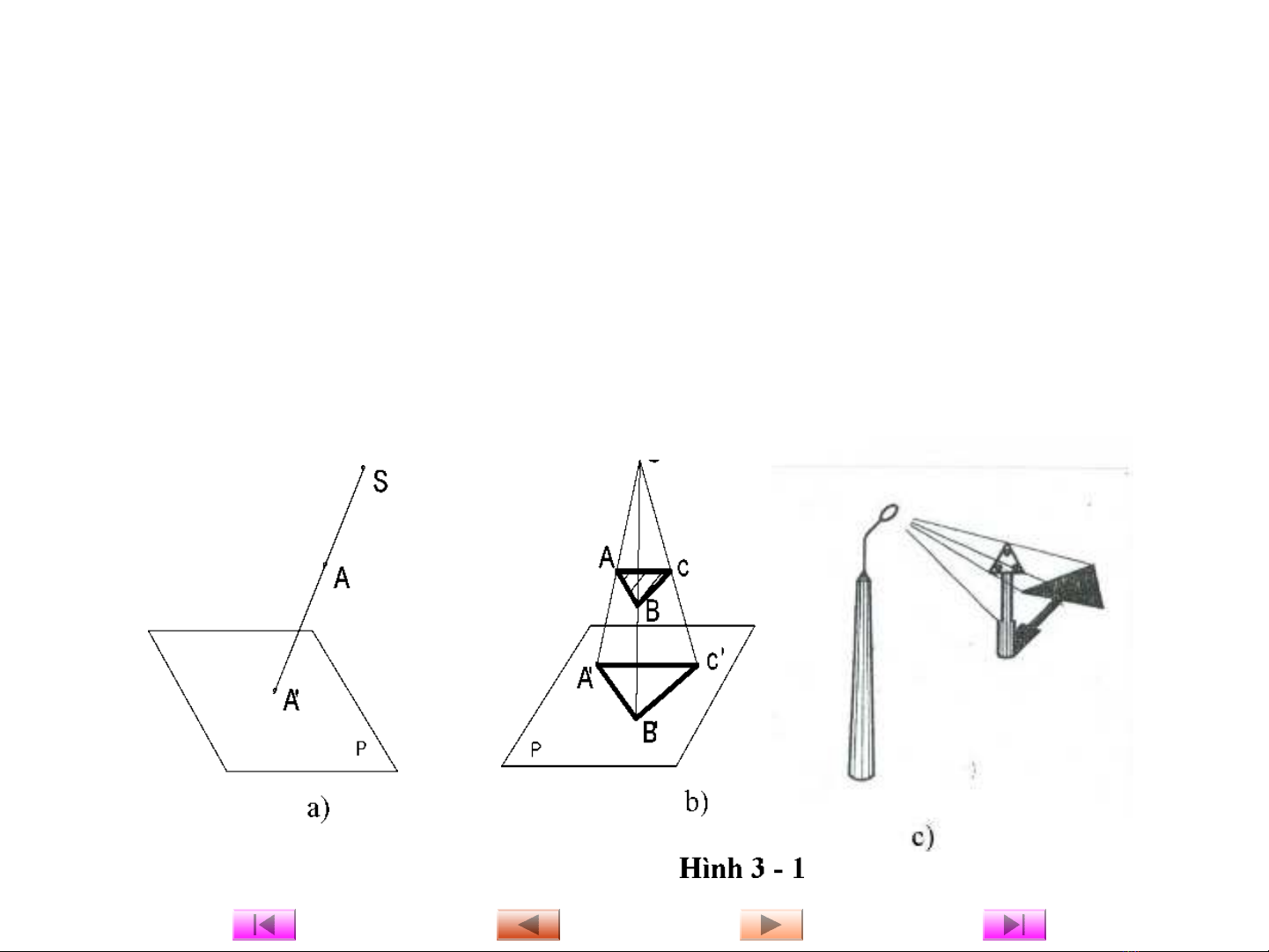
Trong phép chi u xuyên tâm các tia chi u xu t phát t m t đi m. ế ế ấ ừ ộ ể
Đi m này g i là tâm chi u. Hình nh n đc trên m t ph ng g i là ể ọ ế ậ ượ ặ ẳ ọ
m t ph ng chi u, là hình chi u xuyên tâm c a v t th . Phép chi u ặ ẳ ế ế ủ ậ ể ế
xuyên tâm đc dùng trong ki n trúc, xây d ng, h i ho đ v các ượ ế ự ộ ạ ể ẽ
hình chi u ph i c nh.ế ố ả
Các hình chi u xuyên tâm gi ng nh hình nh mà m t ng i nhìn v t ế ố ư ả ắ ườ ậ
th t m t đi m nh t đnh.ể ừ ộ ể ấ ị
I. Khái ni m v các phép chi uệ ề ế
2. Phép chi u song songế
L y m t m t ph ng P và m t đi m ấ ộ ặ ẳ ộ ể
A ngoài P. Ch n m t đng th ng ọ ộ ườ ẳ
đnh h ng s (s không song song v i ị ướ ớ
P)
Qua A d ng m t đng th ng ự ộ ườ ẳ
song song v i s c t P t i A’.ớ ắ ạ
Nh v y ta đã th c hi n m t ư ậ ự ệ ộ
phép chi u và phép chi u đó ế ế
g i là phép chi u song song.ọ ế
P
s
A
A’
I. Khái ni m v các phép chi uệ ề ế