Ch ng 2ươ
Bài 1
a. Tìm kho ng phân li nghi mả ệ
Đ t f(x) = x – sinx – 0,25ặ
Có
f’(x) = 1 – cosx mà -1 <= cosx <= 1 hay 0 <= 1 – cosx <= 2
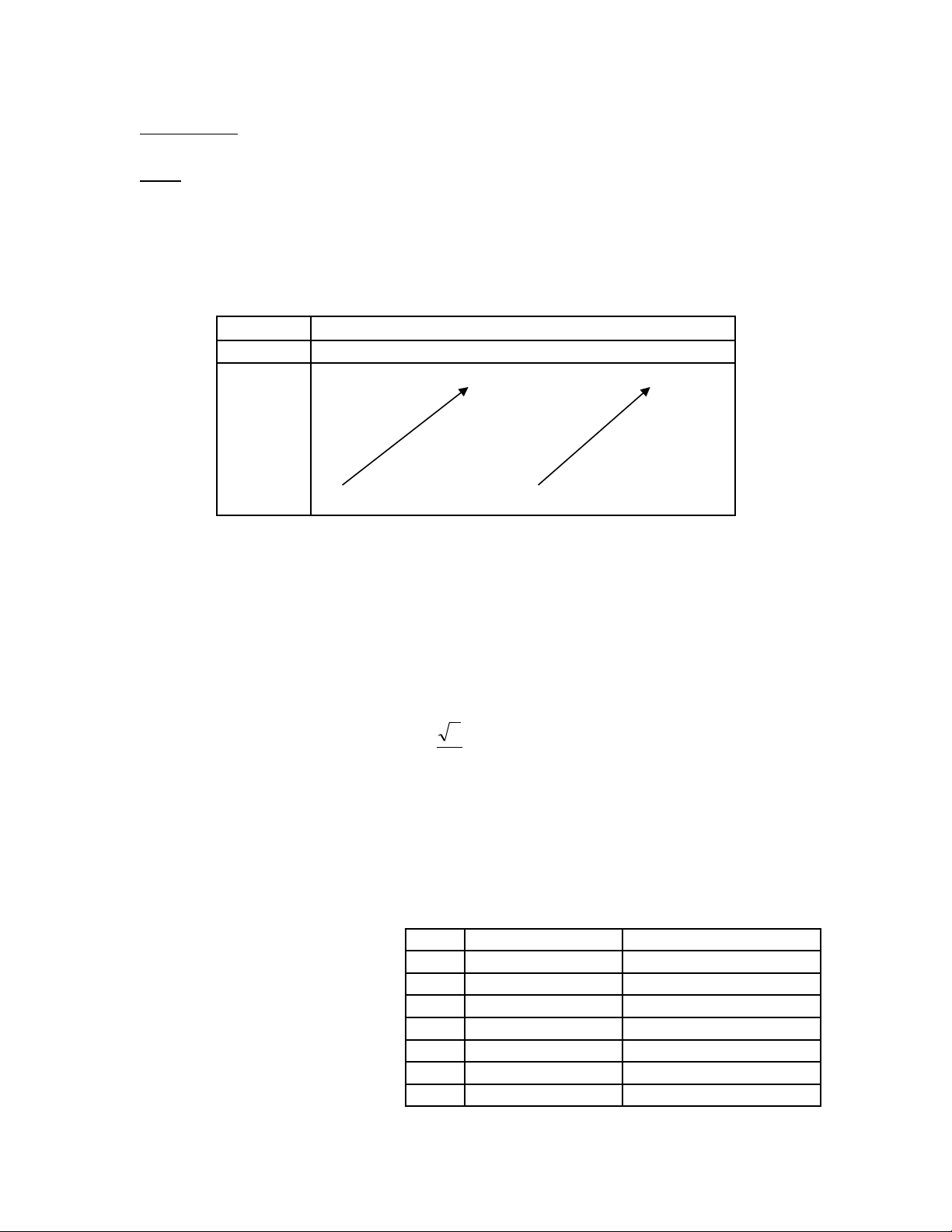
Hàm cosx tu n hoàn v i chu kì 2ầ ớ π nên ta l p b ng bi n thiên c a hàm s trên đo n [-ậ ả ế ủ ố ạ π,
+π]
x-π0π
f’(x) 2 + 0 + 2
f(x)
-π-0,25
-0,25
-0,25
π-0,25
Ta có f(π/4) = -0,1718 < 0
f(π/2) = 0,32 > 0
=> f(π/4).f(π/2) < 0
V y kho ng phân li nghi m c a ph ng trình là [ậ ả ệ ủ ươ π/4, π/2]
b. Ch n ph ng pháp l pọ ươ ặ
T ph ng trình đ u => x = sinx + 0,25ừ ươ ầ
Ch n ọϕ(x) = sinx + 0,25 và ϕ’(x) = cosx
Trong đo n [ạπ/4, π/2] có
1
2
2
)('0 <=≤≤ qx
ϕ
nên ph ng pháp l p h i tươ ặ ộ ụ
Do ϕ’(x) > 0 nên ta ch n xọ0 = π/4
x0 = π/4
xn = ϕ(xn-1) = sin(xn-1) + 0,25
Công th c tính sai s |x – xứ ố n| ≤ q/(1-q).|xn – xn-1|
xn|x – xn|
10.95682518 0.12149875
21.06736662 0.078164602
31.12593311 0.041412762
41.15266954 0.018905511
51.16385116 0.007906599
61.16833423 0.003170009
71.17009942 0.001248178
Qui tròn đ n 2 ch s l th p phân b ng cách vi tế ữ ố ẻ ậ ằ ế
x – 1.17 = (x – x7 + x7 -1.17)
|x – 1.17| ≤ |x – x7| + |x7 – 1.17| = 0,001248178 + 0,009942 = 0,001348
|x – 1.17| ≤ 0,001348 ≤ 0.2.10-2 < 0.5.10-2
C 2 ch s l th p phân trong k t qu này là đáng tinả ữ ố ẻ ậ ế ả
V y có x = 1,17 ậ± 0,002
Bài 2:
a. Tìm kho ng phân li nghi mả ệ
Đ t f(x) = 1,8xặ2 - sin10x (*)
Ta có:
f’(x) = 3,6x – 10cos10x
f’’(x) = 3,6 + 100sin10x
Thay (*) b ng ph ng trình 1,8xằ ươ 2 = sin10x
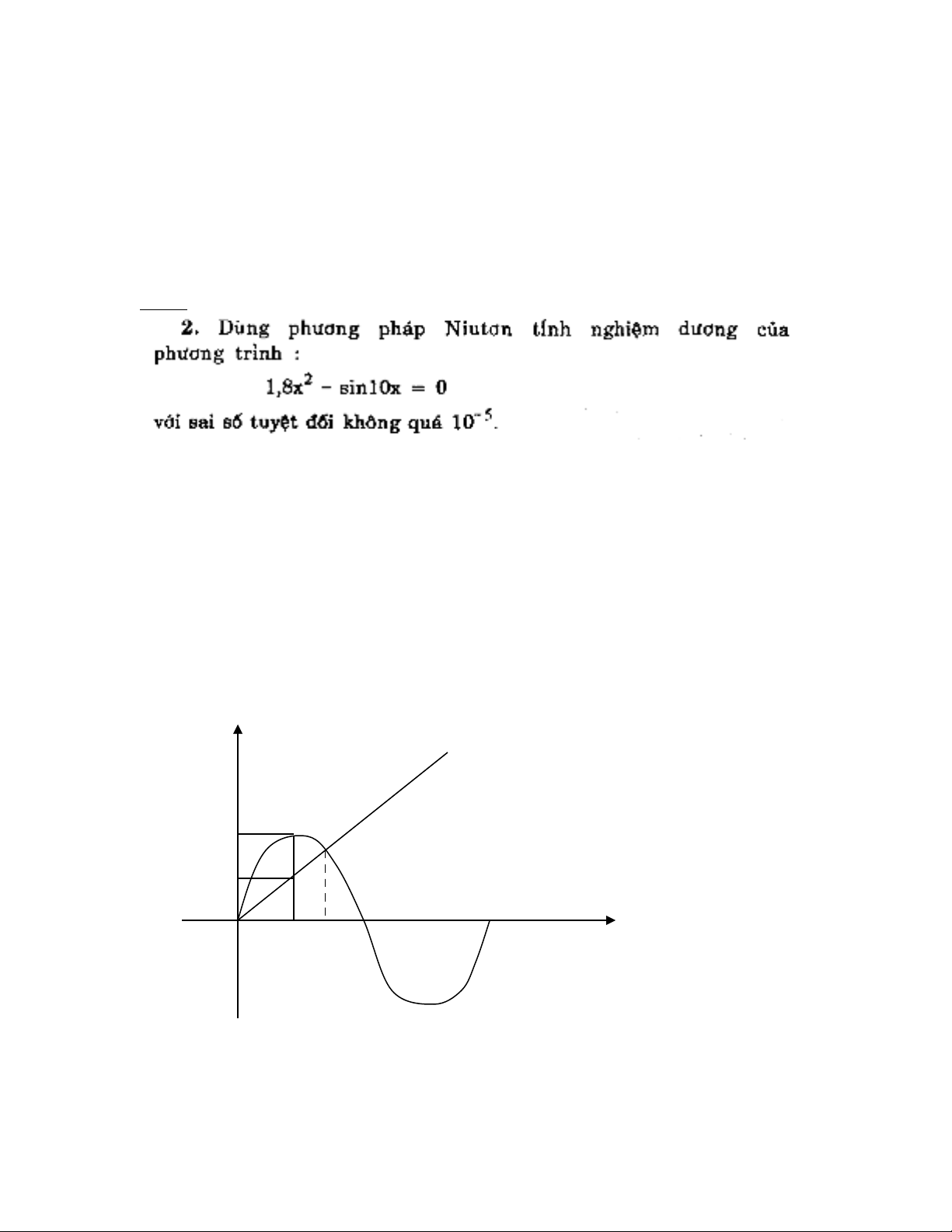
S d ng ph ng pháp đ th ta th y:ử ụ ươ ồ ị ấ
f(π/20) = 18π2/400 – 1 ≈ - 0,96 < 0
f(π/10) = 18π2/100 ≈ 0,18 > 0
V y [ậπ/20; π/10] là kho ng phân li nghi m c a ph ng trìnhả ệ ủ ươ
b. Tìm nghi mệ
Vì f’’(x) > 0, ∀x ∈ [π/20; π/10] nên đ ph ng pháp h i t ta ch n xể ươ ộ ụ ọ 0 = π/10 vì f(π/10)
> 0 cùng d u v i f’’(xấ ớ 0)
π/10 π/5
π/20 x
1
0,44
18x2
sin10x
y
Ta có công th c l pứ ặ
10
10cos106,3
10sin8,1
)('
)(
0
11
1
2
1
1
1
1
1
π
=
−
−
−=−=
−−
−−
−
−
−
−
xvoi
xx
xx
x
xf
xf
xx
nn
nn
n
n
n
nn
Sai s đ c tính theo công th cố ượ ứ
m
xf
xn
n
)(
≤−
α
trong đó
1020
05.0)('
ππ
≤≤>=≥ xmxf
V i sai s tuy t đ i không quá 10ớ ố ệ ố -5 ta có k t qu tính nh sauế ả ư
i xiSai số
0 0,314
10.298198201 0.002252
20.298095328 2.07E-07
Ta có |x – x2| ≤ 2,07.10-7 < 10-5 nên quá trình tính d ng l i ừ ạ
V y nghi m d ng c a ph ng trình tìm đ c là: x = 0,29809 ậ ệ ươ ủ ươ ượ ± 10-5
Bài 3.b
a. Tìm kho ng phân li nghi mả ệ
Đ t f(x) = xặ2 - cosπx
Ta có f’(x) = 2x + πsinπx
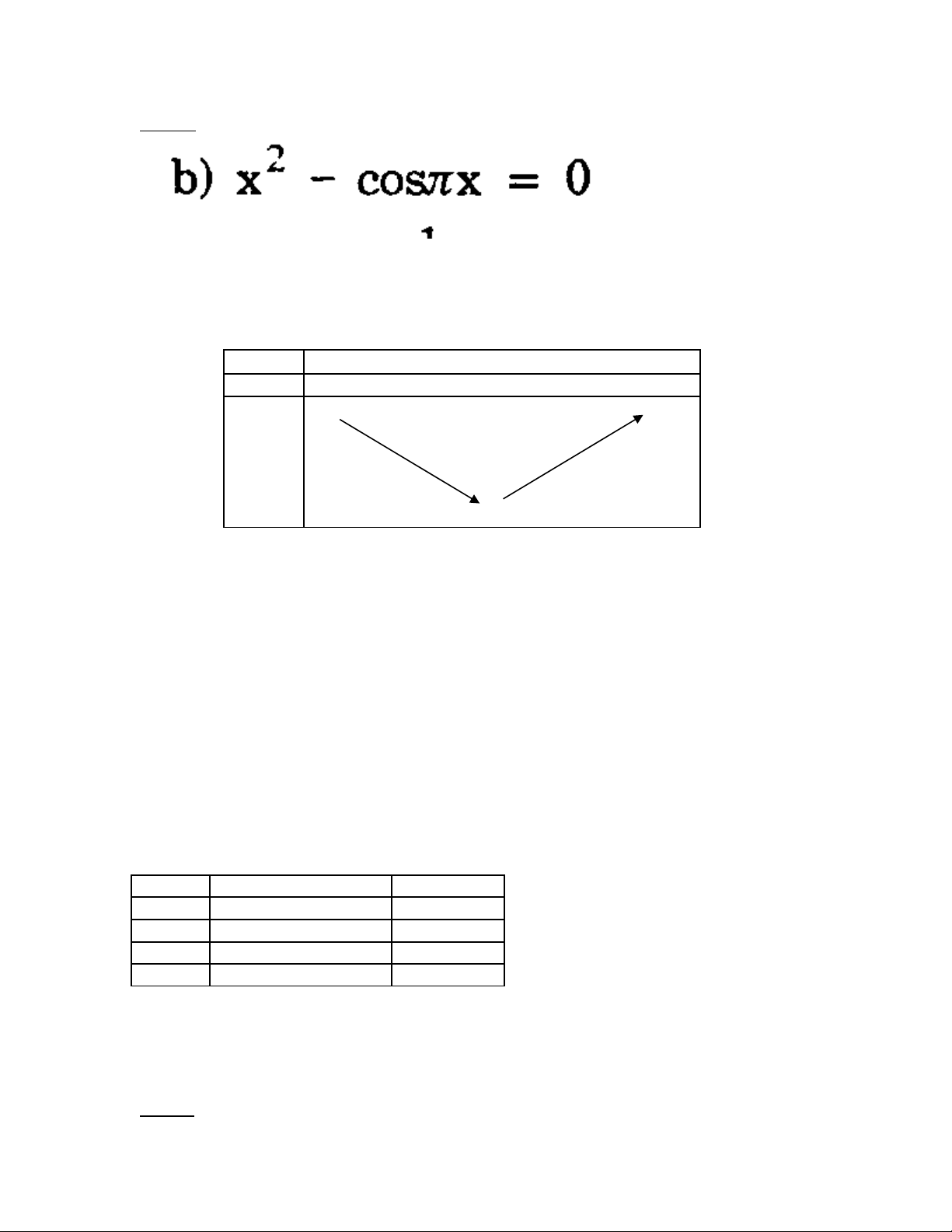
L p b ng bi n thiênậ ả ế
x-∞0+∞
f’(x) + 0 +
f(x)
+∞
-1
+∞
V y đ th c t tr c hoành t i 2 đi m => ph ng trình có 2 nghi m th cậ ồ ị ắ ụ ạ ể ươ ệ ự
Ta có
f(-0,5) = 1 + 0 = 1 > 0
f(0) = -1 < 0
V y kho ng [-0,5; 0] ch a nghi m c a ph ng trìnhậ ả ứ ệ ủ ươ
Ta có
f(0,5) = 1 + 0 = 1 > 0
f(0) = -1 < 0
V y kho ng [0ậ ả ; 0,5] ch a nghi m th hai c a ph ng trìnhứ ệ ứ ủ ươ
b. Tìm nghiêm
•Tìm nghi m trong kho ng [-0,5ệ ả ; 0]
f’’(x) = 2 + π2cosπx > 0 ∀∈[-0,5 ; 0]
Để ph ng pháp h i t ta ch n xươ ộ ụ ọ 0 = 0,5 vì f(0,5) > 0 cùng d u v i f’’(xấ ớ 0)
|f’(x)| >= m = 0,1>0
i xiSai số
0 -0,5
1-0.439806 0.047609
2-0.438605 2.79E-05
3-0.438604 9.7E-12
Ta có |x – x3| ≤ 9,7.10-12 < 10-5 nên quá trình tính d ng l i ừ ạ
V y nghi m th nh t c a ph ng trình tìm đ c là: x = ậ ệ ứ ấ ủ ươ ượ -0,438604 ± 10-5
Bài 3.c
a. Tìm kho ng phân li nghi mả ệ
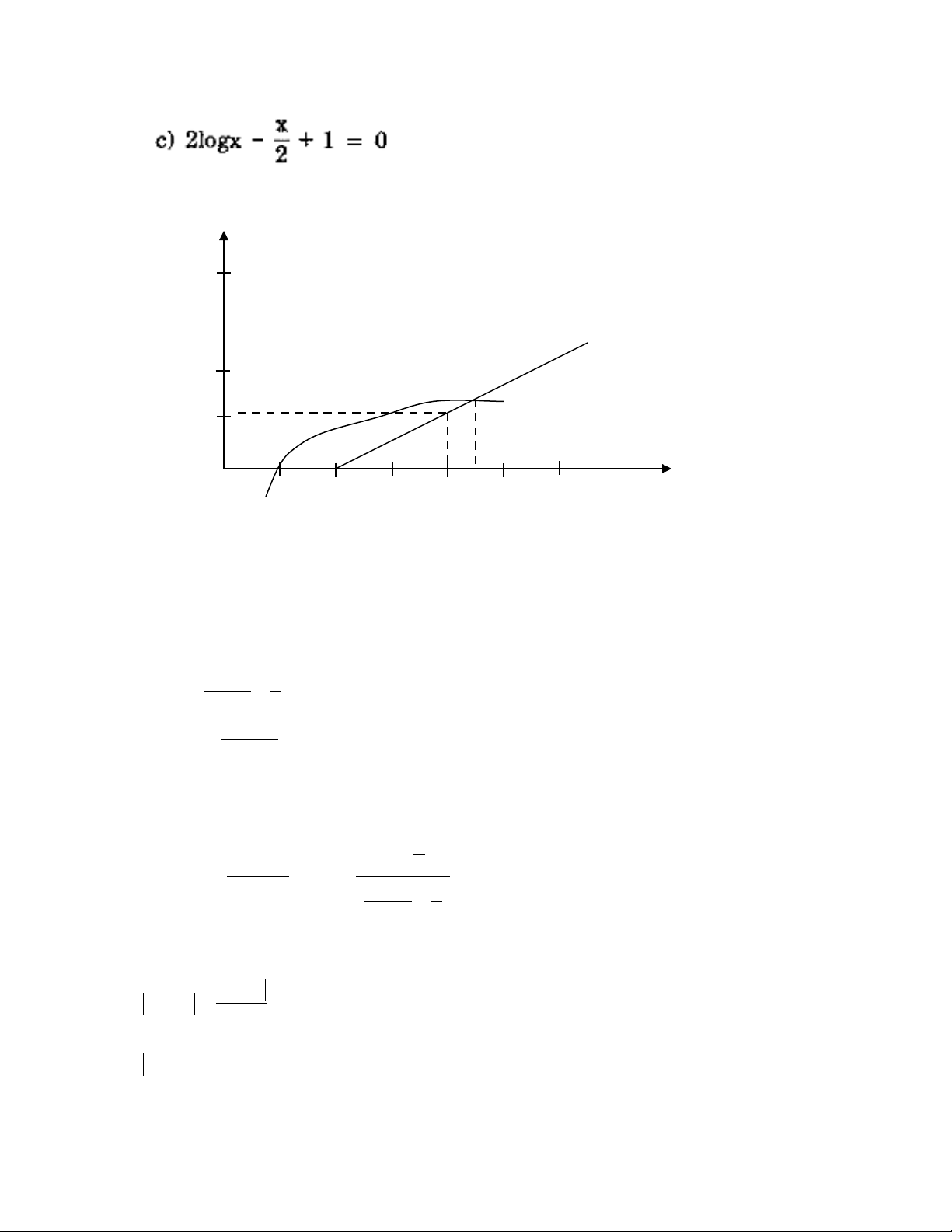
T ph ng trình trên => logx = (x-2)/4ừ ươ
S d ng ph ng pháp đ th ta th yử ụ ươ ồ ị ấ
f(4) ≈ 0,2 > 0
f(5) ≈ -0,1 < 0
V y [4, 5] là kho ng phân li nghi m c a ph ng trìnhậ ả ệ ủ ươ
b. Tìm nghi mệ
2
1
10ln
2
)(' −= x
xf
10ln
2
)('' 2
x
xf −=
Ta th y f’’(x) < 0 ấ∀x ∈[4; 5]. Đ ph ng pháp h i t ta ch n x = 5 vì f(5) < 0 cùngể ươ ộ ụ ọ
d u v i f’’ấ ớ
Ta có công th c l pứ ặ
5
2
1
10ln
2
1
2
lg2
)('
)(
0
1
1
1
1
=
−
+−
−=−= −
−
−
−
xvoi
x
x
x
x
xf
xf
xx n
n
n
nn
Sai s đ c tính theo công th cố ượ ứ
m
xf
xn
n
)(
≤−
α
trong đó
5402.0)(' ≤≤>=≥ xmxf
12 3 45
1
0,5
(x-2)/4
logx