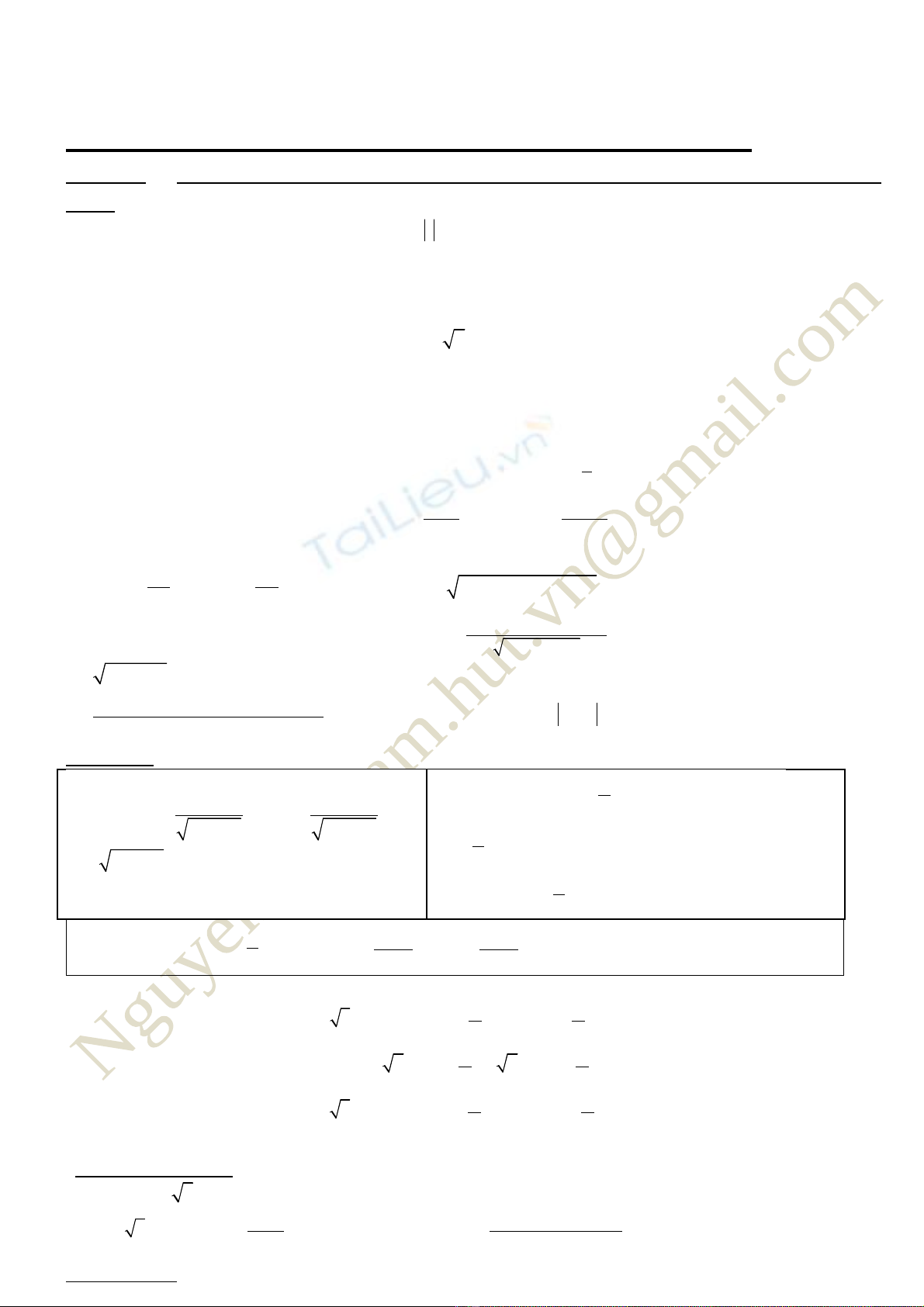
BT Ph ng trươ ình L ng Giác ượ
Các d ng bài t p l ng giácạ ậ ượ
D ng 1ạ Ph ng trình b c nh t và b c hai , b c cao v i 1 hàm s l ngươ ậ ấ ậ ậ ớ ố ượ
giác
Đ t HSLG theo t v i sinx , cosx có đi u ki n ặ ớ ề ệ
t
≤
1
Gi i ph ng trình ……….theo tả ươ
Nh n t tho mãn đi u ki n gi i Pt l ng giác c b n ậ ả ề ệ ả ượ ơ ả
Gi i ph ng trình:ả ươ
1/
2cos2x- 4cosx=1
sinx 0
≥
2/ 4sin3x+3
2
sin2x=8sinx
3/ 4cosx.cos2x +1=0 4/
1-5sinx+2cosx=0
cos 0x
≥
5/ Cho 3sin3x-3cos2x+4sinx-cos2x+2=0 (1) và cos2x+3cosx(sin2x-8sinx)=0 (2).
Tìm n0 c a (1) đ ng th i là nủ ồ ờ 0 c a (2) ( nghi m chung sinx=ủ ệ
1
3
)
6/ sin3x+2cos2x-2=0 7/ a/ tanx+
3
cot x
-2 = 0 b /
+tanx=7
c* / sin6x+cos4x=cos2x
8/sin(
5
22
x
π
+
)-3cos(
7
2
x
π
−
)=1+2sinx 9/
2
sin 2sin 2 2sin 1x x x
− + = −
10/ cos2x+5sinx+2=0 11/ tanx+cotx=4 12/
2 4
sin 2 4cos 2 1 0
2sin cos
x x
x x
+ − =
13/
sin 1 cos 0x x
+ + =
14/ cos2x+3cosx+2=0
15/
2 4
4sin 2 6sin 9 3cos 2 0
cos
x x x
x
+ − − =
16/ 2cosx-
sin x
=1
D ng 2:ạ Ph ng trình b c nh t đ i v i sinx và cosx : asinx+bcosx=cươ ậ ấ ố ớ
Cách 1: asinx+bcosx=c
Đ t cosx=ặ
2 2
a
a b+
; sinx=
2 2
b
a b+
2 2 sin( )a b x c
α
⇒ + + =
Cách : 2
sin cos
b
a x x c
a
+ =
Đ t ặ
[ ]
tan sin cos .tan
ba x x c
a
α α
= ⇒ + =
sin( ) cos
c
xa
α α
⇔ + =
Cách 3: Đ t ặ
tan 2
x
t=
ta có
2
2 2
2 1
sin ;cos
1 1
t t
x x
t t
−
= =
+ +
2
( ) 2 0b c t at b c⇒ + − − + =
Đăc bi t :ệ
1.
sin 3 cos 2sin( ) 2cos( )
3 6
x x x x
π π
+ = + = −
2.
sin cos 2 sin( ) 2 cos( )
4 4
x x x x
π π
± = ± = m
3.
sin 3 cos 2sin( ) 2 cos( )
3 6
x x x x
π π
− = − = − +
Đi u ki n Pt có nghi m : ề ệ ệ
2 2 2
a b c
+ ≥
Gi i ph ng tr nhả ươ ỡ
1/ 2sin15x+
3
cos5x+sin5x=k v i k=0 và k=4 v i k=0ớ ớ
2/ a :
1
3 sin cos cos
x x x
+ =
b:
6
4sin 3cos 6
4sin 3cos 1
x x x x
+ + =
+ +
T Tu n Anhạ ấ
1
BT Ph ng trươ ình L ng Giác ượ
c:
1
3 sin cos 3 3 sin cos 1
x x x x
+ = + + +
3/
cos 7 3 sin 7 2 0x x
− + =
*tìm nghi m ệ
2 6
(;)
5 7
x
π π
∈
4/( cos2x-
3
sin2x)-
3
sinx-cosx+4=0 5/
2
1 cos cos 2 cos 3 2 (3 3 sin )
2cos cos 1 3
x x x x
x x
+ + + = −
+ −
6/
2
cos 2sin .cos 3
2cos sin 1
x x x
x x
−=
+ −
D ng 3ạ Ph ng tr nh đ ng c p đ i v i sinx và cosxươ ỡ ẳ ấ ố ớ
Gi i ph ng tr nhả ươ ỡ
1/a/ 3sin2x-
3
sinxcosx+2cos2x cosx=2 b/ 4 sin2x+3
3
sinxcosx-2cos2x=4
c/3 sin2x+5 cos2x-2cos2x-4sin2x=0 d/ 2 sin2x+6sinxcosx+2(1+
3
)cos2x-5-
3
=0
2/ sinx- 4sin3x+cosx=0 2 cách +/ (tanx -1)(3tan2x+2tanx+1)=0
4
x k
ππ
= +
+ sin3x- sinx+ cosx- sinx=0
⇔
(cosx- sinx)(2sinxcosx+2sin2x+1)=0
3/ tanx sin2x-2sin2x=3(cos2x+sinxcosx)
4/ 3cos4x-4sin2xcos2x+sin4x=0 5/ 4cos3x+2sin3x-3sinx=0
6/ 2 cos3x= sin3x 7/ cos3x- sin3x= cosx+ sinx
8/ sinx sin2x+ sin3x=6 cos3x 9/sin3(x-
π
/4)=
2
sinx
D ng 4ạ Ph ng trình v trái đ i x ng đ i v i sinx và cosxươ ế ố ứ ố ớ
* a(sin x+cosx)+bsinxcosx=c đ t t= sin x+cosx ặ
2t≤
⇒
at + b
21
2
t−
=c
⇔
bt2+2at-2c-b=0
* a(sin x- cosx)+bsinxcosx=c đ t t= sin x- cosx ặ
2t≤
⇒
at + b
2
1
2
t−
=c
⇔
bt2 -2at+2c-b=0
Gi i ph ng tr nh ả ươ ỡ
1/ a/1+tanx=2sinx +
1
cos x
b/ sin x+cosx=
1
tan x
-
1
cot x
2/ sin3x+cos3x=2sinxcosx+sin x+cosx 3/ 1- sin3x+cos3x= sin2x
4/ 2sinx+cotx=2 sin2x+1 5/
2
sin2x(sin x+cosx)=2
6/ (1+sin x)(1+cosx)=2 7/
2
(sin x+cosx)=tanx+cotx
T Tu n Anhạ ấ
Đ ng c p b c 2: asinẳ ấ ậ 2x+bsinx.cosx+c cos2x=0
Cách 1: Th v i cosx=0 V i cosxử ớ ớ
≠
0 .Chia 2 v cho cosế2x ta đ c:ượ
atan2x+btanx +c=d(tan2x+1)
Cách2: áp d ng công th c h b c ụ ứ ạ ậ
Đ ng c p b c 3: asinẳ ấ ậ 3x+b.cos3x+c(sinx+ cosx)=0 ho c ặ
asin3x+b.cos3x+csin2xcosx+dsinxcos2x=0
Xét cos3x=0 và cosx
≠
0 Chia 2 v cho cosế2x ta đ c Pt b c 3 đ i v i tanxượ ậ ố ớ
2
BT Ph ng trươ ình L ng Giác ượ
8/1+sin3 2x+cos32 x=
3
2
sin 4x 9/* a* 3(cotx-cosx)-5(tanx-sin x)=2
9/b*: cos4x+sin4x-2(1-sin2xcos2x) sinxcosx-(sinx+cosx)=0
10/
sin cos 4sin 2 1x x x
− + =
11/ cosx+
1
cos x
+sinx+
1
sin x
=
10
3
12/ sinxcosx+
sin cosx x
+
=1
Dang 5 Gi i phả ư ng trình b ng ph ng pháp h b cơ ằ ươ ạ ậ
Công th c h b c 2ứ ạ ậ
cos2x=
1 cos 2
2
x
+
; sin2x=
1 cos 2
2
x
−
Công th c h b c 3ứ ạ ậ
cos3x=
3cos cos3
4
x x
+
; sin3x=
3sin sin 3
4
x x
−
Gi i ph ng tr nh ả ươ ỡ
1/ sin2 x+sin23x=cos22x+cos24x 2/ cos2x+cos22x+cos23x+cos24x=3/2
3/sin2x+ sin23x-3 cos22x=0
4/ cos3x+ sin7x=2sin2(
5
4 2
x
π
+
)-2cos2
9
2
x
5/ sin24 x+ sin23x= cos22x+ cos2x v iớ
(0; )x
π
∈
6/sin24x-cos26x=sin(
10,5 10x
π
+
) v iớ
(0; )
2
x
π
∈
7/ cos4x-5sin4x=1
8/4sin3x-1=3-
3
cos3x 9/ sin22x+ sin24x= sin26x
10/ sin2x= cos22x+ cos23x 11/ (sin22x+cos42x-1):
sin cosx x
=0
12/ 4sin3xcos3x+4cos3x sin3x+3
3
cos4x=3
;
24 2 8 2
k k
x
π π π π
= + +
13/ 2cos22x+ cos2x=4 sin22xcos2x
14/ cos4xsinx- sin22x=4sin2(
4 2
x
π
−
)-7/2 v i ớ
1x
−
<3
15/ 2 cos32x-4cos3xcos3x+cos6x-4sin3xsin3x=0
16/ sin3xcos3x +cos3xsin3x=sin34x 17/ * 8cos3(x+
3
π
)=cos3x
18/cos10x+2cos24x+6cos3xcosx=cosx+8cosxcos23x
19/
sin 5
5sin
x
x
=1
20 / cos7x+ sin22x= cos22x- cosx 21/ sin2x+ sin22x+ sin23x=3/2
22/ 3cos4x-2 cos23x=1
Dang 6 : Phư ng trình LG gi i b ng các h ng đ ng th cơ ả ằ ằ ẳ ứ
* a3
±
b3=(a
±
b)(a2
m
ab+b2) * a8+ b8=( a4+ b4)2-2 a4b4
* a4- b4=( a2+ b2) ( a2- b2) * a6
±
b6=( a2
±
b2)( a4
m
a 2b2+b4)
Gi i ph ng tr nhả ươ ỡ
1/ sin4
2
x
+cos4
2
x
=1-2sinx 2/ cos3x-sin3x=cos2x-sin2x
3/ cos3x+ sin3x= cos2x 4/
4 4
sin cos 1 (tan cot )
sin 2 2
x x x x
x
+= +
vô nghi m ệ
5/cos6x-sin6x=
13
8
cos22x 6/sin4x+cos4x=
7cot( ) cot( )
8 3 6
x x
π π
+ −
7/ cos6x+sin6x=2(cos8x+sin8x) 8/cos3x+sin3x=cosx-sinx
9/ cos6x+sin6x=cos4x 10/ sinx+sin2x+sin3x+sin4x= cosx+cos2x+cos3x+cos4x
T Tu n Anhạ ấ
3
BT Ph ng trươ ình L ng Giác ượ
11/ cos8x+sin8x=
1
8
12/ (sinx+3)sin4
2
x
-(sinx+3) sin2
2
x
+1=0
Dang 7 : Ph ng trình LG bi n đ i v tích b ng 0ươ ế ổ ề ằ
1/ cos2x- cos8x+ cos4x=1 2/sinx+2cosx+cos2x-2sinxcosx=0
3/sin2x-cos2x=3sinx+cosx-2 4/sin3 x+2cosx-2+sin2 x=0
5/ 3sinx+2cosx=2+3tanx 6/
3
2
sin2x+
2
cos2x+
6
cosx=0
7/ 2sin2x-cos2x=7sinx+2cosx-4 8/
sin 3 sin 5
3 5
x x
=
9/ 2cos2x-8cosx+7=
1
cos x
10/ cos8x+sin8x=2(cos10x+sin10x)+
5
4
cos2x
11/ 1+ sinx+ cos3x= cosx+ sin2x+ cos2x
12/ 1+sinx+cosx+sin2x+cos2x=0 13/ sin2 x(tanx+1)=3sinx(cosx-sinx)+3
14/ 2sin3x-
1
sin x
=2cos3x+
1
cos x
15/cos3x+cos2x+2sinx-2=0
16/cos2x-2cos3x+sinx=0 17/ tanx–sin2x-cos2x+2(2cosx-
1
cos x
)=0
18/sin2x=1+
2
cosx+cos2x 19/1+cot2x=
2
1 cos 2
sin 2
x
x
−
20/ 2tanx+cot2x=2sin2x+
1
sin 2x
21/cosx(cos4x+2)+ cos2x-cos3x=0
22/ 1+tanx=sinx+cosx 23/ (1-tanx)(1+sin2x)=1+tanx
24/ 2
2
sin( )
4
x
π
+
=
1 1
sin cosx x
+
25/ 2tanx+cotx=
2
3sin 2x
+
26/ cotx-tanx=cosx+sinx 27/ 9sinx+6cosx-3sin2x+cos2x=8
Dang 8 : Phư ng trình LG ph i th c hi n công thúc nhân đôi, h b cơ ả ự ệ ạ ậ
cos2x= cos2x- sin2x =2cos2x-1=1-2sin2x
sin2x=2sinxcosx
tan2x=
2
2 tan
1 tan
x
x
−
sinx =
2
2
1
t
t+
; cosx=
2
2
1
1
t
t
−
+
tanx=
2
2
1
t
t−
Gi i ph ng tr nh ả ươ ỡ
1/ sin3xcosx=
1
4
+ cos3xsinx 2/ cosxcos2xcos4xcos8x=1/16
3/tanx+2cot2x=sin2x 4/sin2x(cotx+tan2x)=4cos2x
5/ sin4x=tanx 6/ sin2x+2tanx=3 7/ sin2x+cos2x+tanx=2
8/tanx+2cot2x=sin2x 9/ cotx=tanx+2cot2x
10/a* tan2x+sin2x=
3
2
cotx b* (1+sinx)2= cosx
D ng 9 ạ: Ph ng trình LG ph i th c hi n phép bi n đ i t ng_tích vàươ ả ự ệ ế ổ ổ
tích_t ngổ
Gi i ph ng tr nhả ươ ỡ
1/ sin8x+ cos4x=1+2sin2xcos6x 2/cosx+cos2x+cos3x+cos4x=0
3/
sin 3 sin sin 2 cos 2
1 cos 2
x x x x
x
−= +
−
tìm
( )
0; 2x
π
∈
4/ sinx+sin2x+sin3x+sin4x=0
5/ sin5x+ sinx+2sin2x=1 6/
( )
3 cos 2 cot 2 4sin cos
cot 2 cos 2 4 4
x x x x
x x
π π
+
= + −
−
7/ tanx+ tan2x= tan3x 8/ 3cosx+cos2x- cos3x+1=2sinxsin2x
T Tu n Anhạ ấ
4
BT Ph ng trươ ình L ng Giác ượ
Dang 10 : Ph ng trình LG ph i đ t n ph góc A ho c đ t hàm Bươ ả ặ ẩ ụ ặ ặ
Gi i ph ng tr nhả ươ ỡ
1/ sin(
3
10 2
x
π
−
)=
1
2
sin(
3
10 2
x
π
+
)
3 4 14
2 ; 2 ; 2
5 15 15
x k k k
π π π
π π π
= + + +
2/ sin(
34
x
π
−
)=sin2x sin(
4
x
π
+
)
4 2
x k
π π
= +
3/(cos4x/3 – cos2x):
2
1 tan x
−
=0
3x k
π
=
4/ cosx-2sin(
3
2 2
x
π
−
)=3
4x k
π
=
5/ cos(
7
22
x
π
−
)=sin(4x+3
π
)
;
6 2
k
x k
π π
π
= ± +
6/3cot2x+2
2
sin2x=(2+3
2
)cosx
2 ; 2
3 4
x k k
π π
π π
= ± + ± +
7/2cot2x+
2
2
cos x
+5tanx+5cotx+4=0
4
x k
ππ
= − +
8/ cos2x+
2
1
cos x
=cosx+
1
cos x
x k
π
=
9/sinx- cos2x+
1
sin x
+2
2
1
sin x
=5
7
2 ; 2 ; 2
2 6 6
x k k k
π π π
π π π
= + − + +
11/
1 sin 2
1 sin 2
x
x
+
−
+2
1 tan
1 tan
x
x
+
−
=3
{ }
; , tan 2x k k
π α π α
= + =
Dang 11 : Ph ng trình LG ph i th c hi n các phép bi n đ i ph c t pươ ả ự ệ ế ổ ứ ạ
Gi i ph ng tr nhả ươ ỡ
1/
3 4 6 (16 3 8 2) cos 4cos 3x x
+ − − = −
2
4
x k
ππ
= ± +
2/cos
()
2
3 9 16 80
4x x x
π
− − −
=1 tìm n0 x
∈
Z
{ }
21; 3x
= − −
3/
5cos cos 2x x−
+2sinx=0
2
6
x k
ππ
= − +
4/3cotx- tanx(3-8cos2x)=0
3
x k
ππ
= ± +
5/
( )
2 sin tan 2 cos 2
tan sin
x x x
x x
+− =
−
22
3
x k
ππ
= ± +
6/sin3x+cos3x+ sin3xcotx+cos3xtanx=
2sin 2x
2
4
x k
ππ
= +
7/tan2xtan23 xtan24x= tan2x-tan23 x+tan4x
4
k
x
π
=
8/tanx+tan2x=-sin3xcos2x
2
3
k
x k
ππ π
= +
9/sin3x=cosxcos2x(tan2x+tan2x)
x k
π
=
10/
2
sin sin 1 sin cosx x x x
+ = − −
5 1
;sin 2
x k x
π
−
= =
11/cos2
( )
2
sin 2 cos
4x x
π
+
-1=tan2
2
tan
4
x x
π
+
2
4
x k
ππ
= − +
12/
2 3
2 cos 6 sin 2sin 2sin
5 12 5 12 5 3 5 6
x x x x
π π π π
− − − = − − +
5 5 5
5 ; 5 ; 5
12 3 4
x k k k
π π π
π π π
= − + − + +
Dang 12 : Ph ng trình LG không m u m c, đánh giá 2 v ,t ng 2 l ngươ ẫ ự ế ổ ượ
không âm,v 2 đ th b ng đ o hàm ẽ ồ ị ằ ạ
Gi i ph ng tr nhả ươ ỡ
1/ cos3x+
2
2 cos 3x
−
=2(1+sin22x)
x k
π
=
2/ 2cosx+
2
sin10x=3
2
+2sinxcos28x
4
x k
ππ
= +
3/ cos24x+cos26x=sin212x+sin216x+2 v i xớ
( )
0;
π
∈
4/ 8cos4xcos22x+
1 cos3x−
+1=0
22
3
x k
ππ
= ± +
5/
sin
cos
x
x
π
=
0x
=
6/ 5-4sin2x-8cos2x/2 =3k tìm k
∈
Z* đ h có nghi m 7/ 1-ể ệ ệ
2
2
x
=cosx
8/( cos2x-cos4x)2=6+2sin3x
2
x k
ππ
= +
9/
( )
1
1 cos 1 cos cos 2 sin 4
2
x x x x− + + =
2
4
x k
ππ
= ± +
T Tu n Anhạ ấ
5