Cách khai Phá Dữ Liệu-Các kỹ thuật phân lớp và dự đoán

Chia sẻ: Trần Ngọc Phương | Ngày: | Loại File: PDF | Số trang:78

Thêm vào BST

Báo xấu

234
lượt xem 67
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Một số tên gọi khác của phương pháp học dựa trên các láng giềng gần nhất (Nearest neighbor learning) • Instance-based learning • Lazy learning • Memory-Memory based learning

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Cách khai Phá Dữ Liệu-Các kỹ thuật phân lớp và dự đoán

Khai Phá Dữ Liệu Nguyễn Nhật Quang quangnn-fit@mail.hut.edu.vn Viện Công nghệ Thông tin và Truyền thông Trường Đại học Bách Khoa Hà Nội Năm học 2010-2011
Nội dung môn học: Giới thiệu về Khai phá dữ liệu Giới thiệu về công cụ WEKA Tiền xử lý dữ liệu Phát hiện các luật kết hợp Các kỹ thuật phân lớp và dự đoán thu phân và Học dựa trên các láng giềng gần nhất Học bằng mạng nơ-ron nhân tạo Các kỹ thuật phân nhóm Khai Phá Dữ Liệu 2
Học dựa trên các láng giềng gần nhất Một số tên gọi khác của phương pháp học dựa trên các láng giềng gần nhất (Nearest neighbor learning) • Instance-based learning • Lazy learning • Memory-based learning learning Ý tưởng của phương pháp học dựa trên các láng giềng gần nhất • Với một tập các ví dụ học (Đơn giản là) lưu lại các ví dụ học ─ Không cần xây dựng một mô hình (mô tả) rõ ràng và tổng quát ─ của hàm mục tiêu cần học hàm tiêu • Đối với một ví dụ cần phân loại/dự đoán Xét quan hệ giữa ví dụ đó với các ví dụ học để gán giá trị của ─ hàm mục tiêu (một nhãn lớp, hoặc một giá trị thực) Khai Phá Dữ Liệu 3
Học dựa trên các láng giềng gần nhất Biểu diễn đầu vào của bài toán • Mỗi ví dụ x được biểu diễn là một vectơ n chiều trong không gian các vectơ X∈Rn • x = (x1,x2,…,xn), trong đó xi (∈R) là một số thực Có thể áp dụng được với cả 2 kiểu bài toán học • Bài toán phân lớp (classification) Hàm mục tiêu có giá trị rời rạc (a discrete-valued target function) ─ ─ Đầu ra của hệ thống là một trong số các giá trị rời rạc đã xác định trước (một trong các nhãn lớp) • Bài toán dự đoán/hồi quy (prediction/regression) toán quy (prediction/regression) Hàm mục tiêu có giá trị liên tục (a continuous-valued target function) ─ ─ Đầu ra của hệ thống là một giá trị số thực Khai Phá Dữ Liệu 4
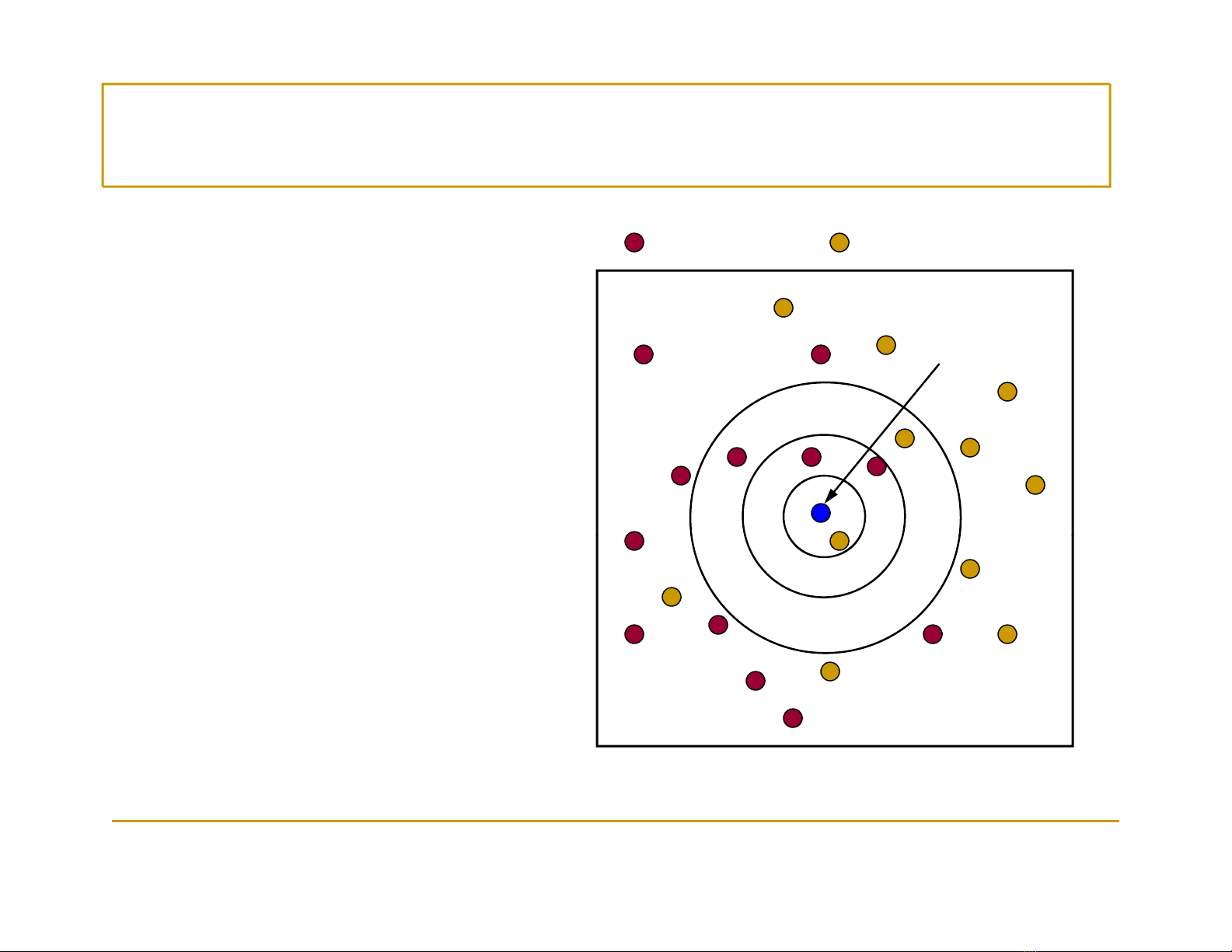
Ví dụ bài toán phân lớp Lớp c1 Lớp c2 Xét 1 láng giềng gần nhất Ví dụ cần phân lớp z → Gán z vào lớp c2 Xét 3 láng giềng gần nhất → Gán z vào lớp c1 Xét 5 láng giềng gần nhất → Gán z vào lớp c1 Khai Phá Dữ Liệu 5
Giải thuật phân lớp k-NN Mỗi ví dụ học x được biểu diễn bởi 2 thành phần: • Mô tả của ví dụ: x=(x1,x2,…,xn), trong đó xi∈R • Nhãn lớp : c (∈C, với C là tập các nhãn lớp được xác định trước) Giai đoạn học • Đơn giản là lưu lại các ví dụ học trong tập học: D = {x} Giai đoạn phân lớp: Để phân lớp cho một ví dụ (mới) z • Với mỗi ví dụ học x∈D, tính khoảng cách giữa x và z • Xác định tập NB(z) – các láng giềng gần nhất của z → Gồm k ví dụ học trong D gần nhất với z tính theo một hàm trong nh theo hàm khoảng cách d • Phân z vào lớp chiếm số đông (the majority class) trong số các lớp của các ví dụ học trong NB(z) NB( Khai Phá Dữ Liệu 6
Giải thuật dự đoán k-NN Mỗi ví dụ học x được biểu diễn bởi 2 thành phần: • Mô tả của ví dụ: x=(x1,x2,…,xn), trong đó xi∈R • Giá trị đầu ra mong muốn: yx∈R (là một số thực) Giai đoạn học • Đơn giản là lưu lại các ví dụ học trong tập học D Giai đoạn dự đoán: Để dự đoán giá trị đầu ra cho ví dụ z • Đối với mỗi ví dụ học x∈D, tính khoảng cách giữa x và z • Xác định tập NB(z) – các láng giềng gần nhất của z → Gồm k ví dụ học trong D gần nhất với z tính theo một hàm khoảng trong nh theo hàm kho cách d 1 • Dự đoán giá trị đầu ra đối với z: y z = ∑ y x∈NB ( z ) x k Khai Phá Dữ Liệu 7
Một hay nhiều láng giềng gần nhất? Việc phân lớp (hay dự đoán) chỉ dựa trên duy nhất một láng giềng gần nhất (là ví dụ học gần nhất với ví dụ cần phân lớp/dự đoán) thường không chính xác • Nếu ví dụ học này là một ví dụ bất thường, không điển hình (an outlier) – rất khác so với các ví dụ khác • Nếu ví dụ học này có nhãn lớp (giá trị đầu ra) sai – do lỗi trong quá trình thu thập (xây dựng) tập dữ liệu Thường xét k (>1) các ví dụ học (các láng giềng) gần nhất với ví dụ cần phân lớp/dự đoán Đố Đối với bài toán phân lớp có 2 lớp, k thường được chọn là đượ ch là bài toán phân có một số lẻ, để tránh cân bằng về tỷ lệ các ví dụ giữa 2 lớp • Ví dụ: k= 3, 5, 7,… Khai Phá Dữ Liệu 8
Hàm tính khoảng cách (1) Hàm tính khoảng cách d • Đóng vai trò rất quan trọng trong phương pháp học dựa trên các láng giềng gần nhất • Thường được xác định trước, và không thay đổi trong suốt quá trình học và phân loại/dự đoán trình và phân lo Lựa chọn hàm khoảng cách d • Các hàm khoảng cách hình học: Dành cho các bài toán có các hà kh hì Dà bài thuộc tính đầu vào là kiểu số thực (xi∈R) • Hàm khoảng cách Hamming: Dành cho các bài toán có các thuộc tính đầu vào là kiểu nhị phân (xi∈{0,1}) • Hàm tính độ tương tự Cosine: Dành cho các bài toán phân lớp văn bản (xi là giá trị trọng số TF/IDF của từ khóa thứ i) Khai Phá Dữ Liệu 9
Hàm tính khoảng cách (2) Các hàm tính khoảng cách hình học (Geometry distance functions) 1/ p ⎛n p⎞ d ( x, z ) = ⎜ ∑ xi − zi ⎟ Hàm Minkowski (p-norm): • ⎝ i =1 ⎠ n d ( x, z ) = ∑ xi − zi Hàm Manhattan (p=1): • i =1 n ∑ (x − z ) Hàm Euclid (p=2): d ( x, z ) = 2 • i i i =1 1/ p ⎛n p⎞ Hàm Chebyshev (p=∞): d ( x, z ) = lim ⎜ ∑ xi − zi ⎟ Chebyshev • ⎝ i =1 ⎠ p →∞ = max xi − zi i Khai Phá Dữ Liệu 10
Hàm tính khoảng cách (3) Hàm khoảng cách n d ( x, z ) = ∑ Difference ( xi , z i ) Hamming Hamming i =1 ⎧1, if ( a ≠ b) • Đối với các thuộc tính đầu Difference ( a, b) = ⎨ vào là kiểu nhị phân ({0,1}) ⎩0, if ( a = b) • Ví dụ: x=(0,1,0,1,1) n ∑x z Hàm tính độ tương tự ii x.z d ( x, z ) = = i =1 Cosine xz n n ∑ xi ∑ zi 2 2 • Đối với đầu vào là một vectơ ố i =1 i =1 các giá trị trọng số (TF/IDF) của các từ khóa Khai Phá Dữ Liệu 11
Chuẩn hóa miền giá trị thuộc tính n (xi − zi )2 ∑ Hàm tính khoảng cách Euclid: d ( x, z ) = i =1 Giả sử mỗi ví dụ được biểu diễn bởi 3 thuộc tính: Age, Income (cho mỗi tháng), và Height (đo theo mét) • x = (Age=20, Income=12000, Height=1.68) • z = (Age=40, Income=1300, Height=1.75) Khoảng cách giữa x và z • d(x,z) = [(20-40)2 + (12000-1300)2 + (1.68-1.75)2]1/2 [(20 (12000 (1 • Giá trị khoảng cách bị quyết định chủ yếu bởi giá trị khoảng cách (sự khác biệt) giữa 2 ví dụ đối với thuộc tính Income → Vì: Thuộc tính Income có miền giá trị rất lớn so với các thuộc tính khác Thu tính Income mi giá tr so các thu tính khác Cần phải chuẩn hóa miền giá trị (đưa về cùng một khoảng giá trị) • Khoảng giá trị [0,1] thường được sử dụng • Đối với mỗi thuộc tính i: xi = xi/max(fi) th tí Khai Phá Dữ Liệu 12
Trọng số của các thuộc tính n (xi − zi )2 ∑ d ( x, z ) = Hàm khoảng cách Euclid: i =1 • Tất cả các thuộc tính có cùng (như nhau) ảnh hưởng đối với giá trị khoảng cách Các thuộc tính khác nhau có thể (nên) có mức độ ảnh hưởng độ Các thu tính khác nhau th (nên) có khác nhau đối với giá trị khoảng cách Cần phải tích hợp (đưa vào) các giá trị trọng số của các thuộc tính trong hàm tính khoảng cách trong hàm tính kho cách n ∑ wi (xi − zi ) d ( x, z ) = 2 • wi là trọng số của thuộc tính i: i =1 Làm sao để xác định các giá trị trọng số của các thuộc tính? sao để xác đị các giá tr tr các thu tính? • Dựa trên các tri thức cụ thể của bài toán (vd: được chỉ định bởi các chuyên gia trong lĩnh vực của bài toán đang xét) • Bằng một quá trình tối ưu hóa các giá trị trọng số (vd: sử dụng một tập quá trình hóa các giá tr tr (vd: học để học một bộ các giá trị trọng số tối ưu) Khai Phá Dữ Liệu 13
Khoảng cách của các láng giềng (1) Xét tập NB(z) – gồm k ví dụ học gần Test instance z nhất với ví dụ cần phân lớp/dự đoán z nh ví phân • Mỗi ví dụ (láng giềng gần nhất) này có khoảng cách khác nhau đến z • Các láng giềng này có ảnh hưởng như nhau đối với việc phân lớp/dự đoáncho z? → KHÔNG! Cần gán các mức độ ảnh hưởng (đóng góp) của mỗi láng giềng gần nhất tùy theo khoảng cách của nó đến z nó đế theo kho cách • Mức độ ảnh hưởng cao hơn cho các láng giềng gần hơn! Khai Phá Dữ Liệu 14
Khoảng cách của các láng giềng (2) Gọi v là hàm xác định trọng số theo khoảng cách • Đối với một giá trị d(x,z) – khoảng cách giữa x và z • v(x,z) tỷ lệ nghịch với d(x,z) ∑ v( x, z ).Identical (c j , c( x)) Đối với bài toán phân lớp: c ( z ) = arg max c j ∈C x∈NB ( z ) ⎧1, if (a = b) Identical (a, b) = ⎨ ⎩0, if (a ≠ b) ∑ v( x, z ). f ( x) Đối với bài toán dự đoán (hồi quy): x∈NB ( z ) f ( z) = ∑ v ( x, z ) x∈NB ( z ) Lựa chọn một hàm xác định trọng số theo khoảng cách: d ( x, z )2 − 1 1 v ( x, z ) = e σ2 v ( x, z ) = v ( x, z ) = α + d ( x, z ) α + [d ( x, z )]2 Khai Phá Dữ Liệu 15
Lazy learning vs. Eager learning Lazy learning. Việc đánh giá hàm mục tiêu (target function) được hoãn lại cho đến khi xét ví dụ cần phân loại/dự đoán • Đánh giá (xấp xỉ) hàm mục tiêu một cách cục bộ (locally) và riêng rẽ (diferrently) cho mỗi ví dụ cần phân loại/dự đoán (tại thời điểm phân loại/dự đoán của hệ thống) • Tính toán nhiều lần các xấp xỉ cục bộ của hàm mục tiêu hà tiê • Thường mất thời gian lâu hơn để đưa ra kết luận (phân lớp/dự đoán), và cần nhiều không gian nhớ hơn • Ví dụ: Nearest neighbor learner, Locally weighted regression Nearest neighbor learner Locally weighted regression Eager learning. Việc đánh giá hàm mục tiêu được hoàn thành trước khi xét đến bất kỳ ví dụ cần phân loại/dự đoán • Đánh giá (xấp xỉ) hàm mục tiêu một cách tổng thể (globally) đối với toàn bộ không gian các ví dự (tại thời điểm học của hệ thống) • Tính toán một xấp xỉ duy nhất (ở mức tổng thể) của hàm mục tiêu • Ví dụ: Linear regression, Support vector machines, Neural networks, etc. Khai Phá Dữ Liệu 16
Mạng nơ-ron nhân tạo – Giới thiệu (1) Mạng nơ-ron nhân tạo (Artificial neural network – ANN) Mô phỏng các hệ thống nơ-ron sinh học (các bộ não con người) ph các th sinh (các não con ng ANN là một cấu trúc (structure/network) được tạo nên bởi một số lượng các nơ-ron (artificial neurons) liên kết với nhau Mỗi nơ-ron Có một đặc tính vào/ra Thực hiện một tính toán cục bộ (một hàm cục bộ) Th hi tí hà Giá trị đầu ra của một nơ-ron được xác định bởi Đặ tính vào/ra Đặc tính vào/ra của nó nó Các liên kết của nó với các nơ-ron khác (Có thể) các đầu vào bổ sung Khai Phá Dữ Liệu 17
Mạng nơ-ron nhân tạo – Giới thiệu (2) ANN có thể được xem như một cấu trúc xử lý thông tin một cách phân tán và song song ở mức cao ANN có khả năng học (learn), nhớ lại (recall), và khái quát hóa (generalize) từ các dữ liệu học –bằng cách gán và điều chỉnh (thích nghi) các giá trị trọng số (mức độ quan trọng) của các liên kết giữa các nơ-ron Chức năng (hàm mục tiêu) của một ANN được xác định bởi đị Ch (hà tiê ANN Kiến trúc (topology) của mạng nơ-ron Đặc tính vào/ra của mỗi nơ-ron tính vào/ra Chiến lược học (huấn luyện) Dữ liệu học Khai Phá Dữ Liệu 18
ANN – Các ứng dụng điển hình (1) Xử lý ảnh và Computer vision Ví dụ: So khớp, tiền xử lý, phân đoạn và phân tích ảnh, computer vision, So kh ti lý phân và phân tích computer vision nén ảnh, xử lý và hiểu các ảnh thay đổi theo thời gian Xử lý tín hiệu Ví dụ: Phân tích tín hiệu và hình thái địa chấn, động đất hì thái đị độ đấ Ví Phâ tí tí hi Nhận dạng mẫu Ví dụ: Trích chọn thuộc tính, phân loại và phân tích tín hiệu ra-đa, nhận Trích ch thu tính phân lo và phân tích tín hi ra nh dạng và hiểu giọng nói, nhận dạng dấu vân tay, nhận dạng ký tự (chữ hoặc số), nhận dạng mặt người, và phân tích chữ viết tay Y tế Ví dụ: Phân tích và hiểu tín hiệu điện tim, chẩn đoán các loại bệnh, và xử lý các ảnh trong lĩnh vực y tế Khai Phá Dữ Liệu 19
ANN – Các ứng dụng điển hình (2) Các hệ thống quân sự Ví dụ: Phát hiện thủy lôi, phân loại nhiễu ra-đa Phát hi th lôi phân lo nhi ra Các hệ thống tài chính Ví dụ: Phân tích thị trường chứng khoán, đánh giá giá trị bất động sản, kiểm tra truy cập thẻ tín dụng, kinh doanh cổ phiếu ki tra truy th tín kinh doanh phi Lập kế hoạch, điều khiển, và tìm kiếm Ví dụ: Cài đặt song song các bài toán thỏa mãn ràng buộc, tìm lời giải cho bài toán người đưa hàng, điều khiển và khoa học nghiên cứu về bài hà khi kh người máy (robotics) Các hệ thống năng lượng Ví dụ: Đánh giá trạng thái hệ thống, phát hiện và khắc phục sự cố, dự đoán tải (khối lượng) công việc, và đánh giá mức độ an toàn ...(và nhiều lĩnh vực bài toán khác!) bà toá Khai Phá Dữ Liệu 20