Cấu trúc cây (Tree)
C
Cấấu tr
u trú
úc cây (Tree)
c cây (Tree)
Chương 6
Cây nhiề u nhánh
4
Các khái niệ m cơ bả n
1
Cây nhị phân tìm kiế m
2
Cây nhị phân cân bằ ng
3
N
Nộội dung
i dung
3/11/2010 www.lhu.edu.vn
Chư ơ ng
Chư ơ ng 6 C
6 Cấấu tr
u trú
úc cây
c cây
Ví dụ : bài toán đư a thư
Có mộ t bứ c thư cầ n chuyể n đế n đị a chỉ
“Nguyễ n Văn A, 10 Huỳnh Văn Nghệ , Biên hoà, Đồ ng
Nai, Việ t nam”
Trên thế giớ i hiệ n có khoả ng 8 tỷ ngư ờ i
Làm thế nào để tìm ra ngư ờ i A nhanh nhấ t?
Dùng cấ u trúc mả ng ??
Dùng danh sách liên kế t ??
C
Cá
ác kh
c khá
ái ni
i niệệm cơ b
m cơ bảản
n
3/11/2010 www.lhu.edu.vn
Chư ơ ng
Chư ơ ng 6 C
6 Cấấu tr
u trú
úc cây
c cây
C
Cá
ác kh
c khá
ái ni
i niệệm cơ b
m cơ bảản
n
3/11/2010 www.lhu.edu.vn
Chư ơ ng
Chư ơ ng 6 C
6 Cấấu tr
u trú
úc cây
c cây
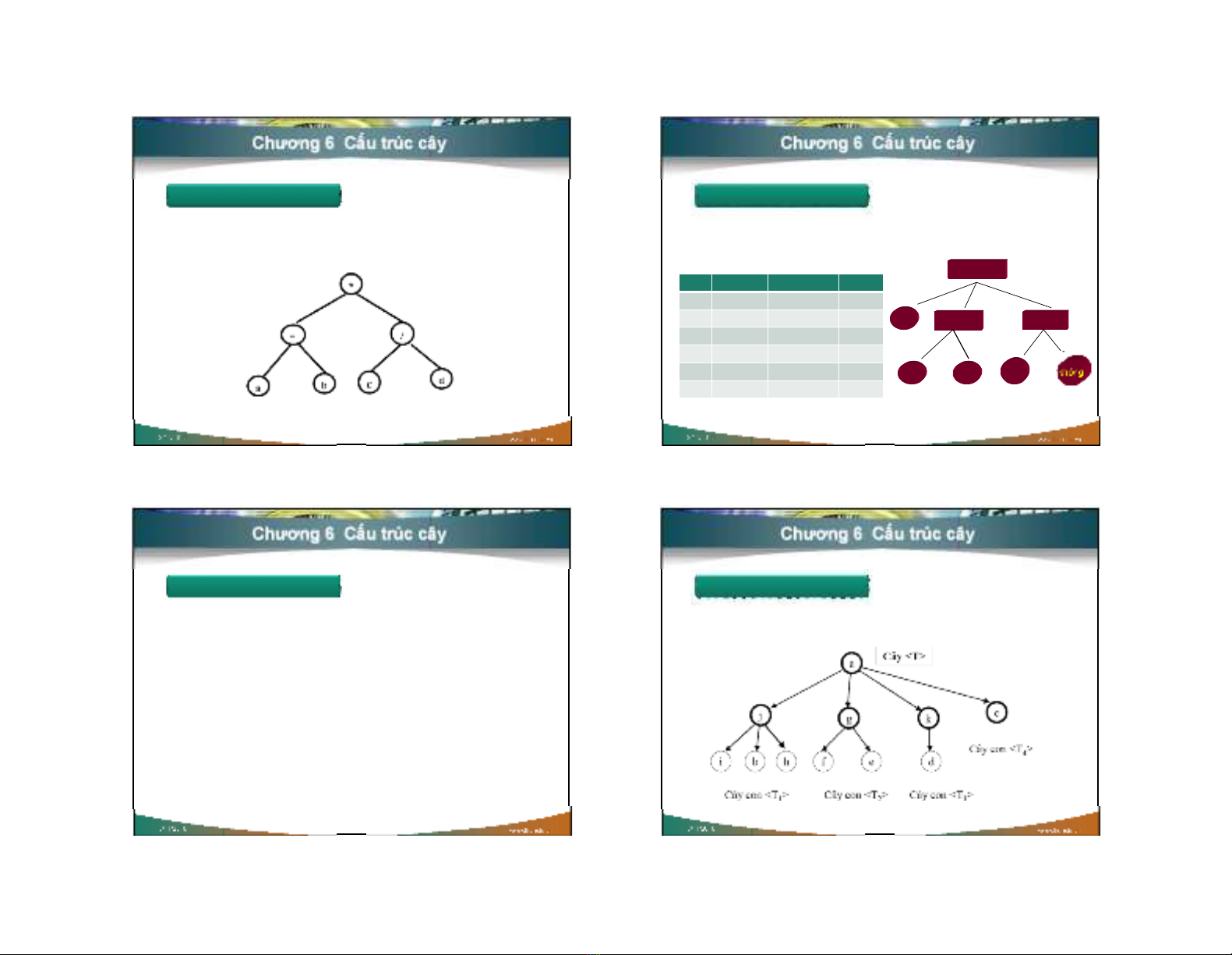
Ví dụ : cây thư mụ c windows
C
Cá
ác kh
c khá
ái ni
i niệệm cơ b
m cơ bảản
n
3/11/2010 www.lhu.edu.vn
Chư ơ ng
Chư ơ ng 6 C
6 Cấấu tr
u trú
úc cây
c cây
Ví dụ : cây biể u thứ c (a+b)/(c-d)
C
Cá
ác kh
c khá
ái ni
i niệệm cơ b
m cơ bảản
n
3/11/2010 www.lhu.edu.vn
Chư ơ ng
Chư ơ ng 6 C
6 Cấấu tr
u trú
úc cây
c cây
Ví dụ : cây quyế t đị nh
C
Cá
ác kh
c khá
ái ni
i niệệm cơ b
m cơ bảản
n
Nhiệt độ
Có
Đau đầu
Bình thư ờng Cao Rất cao
Đau đầu
không
không Có không
có
{e2} không
{e5}
có
{e3}
không
{e6}
{e1, e4} {e2, e5} {e3,e6}
Đau đầ u Nhiệ t độ Cúm
e1 Có Bình thư ờ ng Không
e2 Có Cao Có
e3 Có Rấ t cao Có
e4 Không Bình thư ờ ng Không
e5 Không Cao Không
e6 Không Rấ t cao Không
3/11/2010 www.lhu.edu.vn
Chư ơ ng
Chư ơ ng 6 C
6 Cấấu tr
u trú
úc cây
c cây
Đị nh nghĩa
Mộ t cây <T> (Tree) là:
Mộ t tậ p các phầ n tử , gọ i là các nút (Node):
p1,p2,…,pN
Nế u N=0, cây <T> gọ i là cây rỗ ng (NULL)
Nế u N>0:
• Tồ n tạ i duy nhấ t 1 nút pk gọ i là gố c củ a cây
• Các nút còn lạ i đư ợ c chia thành m tậ p không giao nhau: T1,
T2, …, Tm
• Mỗ i <Ti> là 1 cây con củ a cây <T>
C
Cá
ác kh
c khá
ái ni
i niệệm cơ b
m cơ bảản
n
3/11/2010 www.lhu.edu.vn
Chư ơ ng
Chư ơ ng 6 C
6 Cấấu tr
u trú
úc cây
c cây
Ví dụ : cây nhiề u nhánh
C
Cá
ác kh
c khá
ái ni
i niệệm cơ b
m cơ bảản
n

3/11/2010 www.lhu.edu.vn
Chư ơ ng
Chư ơ ng 6 C
6 Cấấu tr
u trú
úc cây
c cây
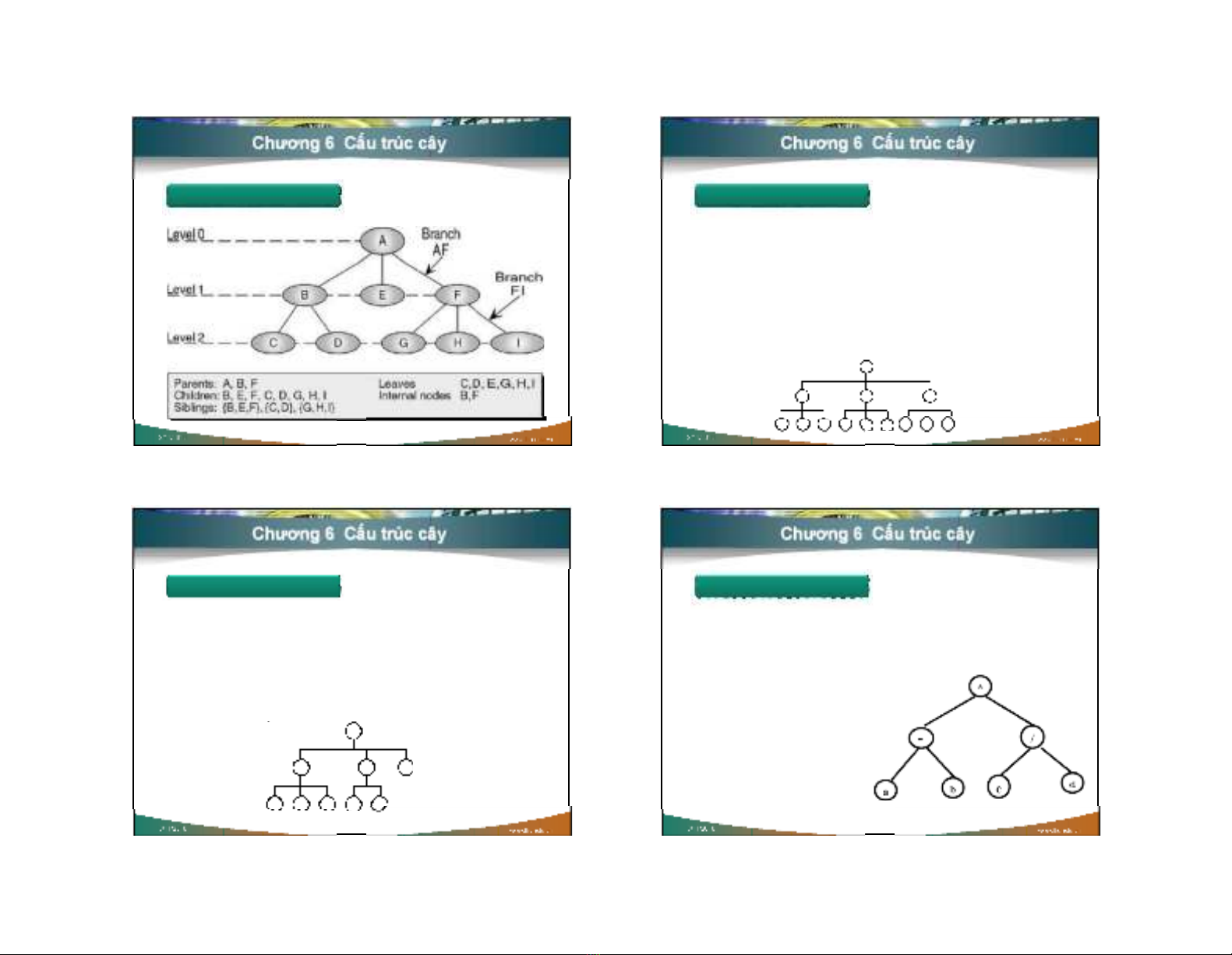
Nút (Node): là 1 phầ n tử trong cây. Mỗ i nút có
thể chứ a 1 dữ liệ u bấ t kỳ
Nhánh (Branch): là đoạ n nố i giữ a 2 nút
Nút cha (Parent node)
Nút con (Child node)
Nút anh em (Sibling nodes): là nhữ ng nút có
cùng nút cha
C
Cá
ác kh
c khá
ái ni
i niệệm cơ b
m cơ bảản
n
3/11/2010 www.lhu.edu.vn
Chư ơ ng
Chư ơ ng 6 C
6 Cấấu tr
u trú
úc cây
c cây
Bậ c củ a 1 nút pi: là số nút con củ a pi
Ví dụ trên : Bậ c (a) = 4; Bậ c (j) = 3; Bậ c (g) = 2;
Bậ c (k) = 1; Bậ c (c) = 0
Nút gố c (Root node): nút không có nút cha
Nút lá (Leaf node, hay nút ngoài – External
node): là nút có bậ c = 0 (không có nút con)
Nút nộ i (Internal node): là nút có nút cha và có
nút con
Cây con (Subtree)
C
Cá
ác kh
c khá
ái ni
i niệệm cơ b
m cơ bảản
n
3/11/2010 www.lhu.edu.vn
Chư ơ ng
Chư ơ ng 6 C
6 Cấấu tr
u trú
úc cây
c cây
Bậ c củ a cây: là bậ c lớ n nhấ t củ a các nút trong
cây
Bậ c (<T>) = max {bậ c (pi) / pi Î <T>}
Bậ c củ a cây <T> ?
Đư ờ ng đi (Path) giữ a nút pi đế n nút pj: là dãy
các nút liên tiế p từ pi đế n pj sao cho giữ a hai nút
kề nhau đề u có nhánh
Path(a, d) ?
C
Cá
ác kh
c khá
ái ni
i niệệm cơ b
m cơ bảản
n
3/11/2010 www.lhu.edu.vn
Chư ơ ng
Chư ơ ng 6 C
6 Cấấu tr
u trú
úc cây
c cây
Mứ c (Level):
Mứ c (p) = 0 nế u p = root
Mứ c (p) = 1 + Mứ c (Cha (p)) nế u p!=root
Chiề u cao củ a cây (Height - hT): đư ờ ng đi dài
nhấ t từ nút gố c đế n nút lá
hT = max {Path(root, pi) / pi là nút lá Î <T>}
C
Cá
ác kh
c khá
ái ni
i niệệm cơ b
m cơ bảản
n
3/11/2010 www.lhu.edu.vn
Chư ơ ng
Chư ơ ng 6 C
6 Cấấu tr
u trú
úc cây
c cây
C
Cá
ác kh
c khá
ái ni
i niệệm cơ b
m cơ bảản
n
3/11/2010 www.lhu.edu.vn
Chư ơ ng
Chư ơ ng 6 C
6 Cấấu tr
u trú
úc cây
c cây
C
Cá
ác kh
c khá
ái ni
i niệệm cơ b
m cơ bảản
n
Cây đầ y đủ (Full tree): là 1 cây thoả
•Tấ t cả các nút lá đề u nằ m trên cùng 1 mứ c
•Tấ t cả nhữ ng nút khác có cùng bậ c vớ i cây
•Mứ c h củ a cây đầ y đủ bậ c d có dh nút
VD. mứ c h=2 củ a cây bậ c 3 có bao nhiêu nút ?
•h mứ c đầ u tiên củ a cây đầ y đủ bậ c d có số nút là:
1 + d + d2+ d3+ … + dh-1 = (dh- 1)/(d – 1)
3 mứ c đầ u tiên củ a cây đầ y đủ bậ c 3 có bao nhiêu nút ?
3/11/2010 www.lhu.edu.vn
Chư ơ ng
Chư ơ ng 6 C
6 Cấấu tr
u trú
úc cây
c cây
C
Cá
ác kh
c khá
ái ni
i niệệm cơ b
m cơ bảản
n
Cây hoàn chỉ nh (Complete tree) vớ i h mứ c:
là 1 cây thoả các điề u kiệ n
•Nhữ ng nút từ mứ c 0 đế n mứ c h-1 đề u đầ y đủ
•Nhữ ng nút ở mứ c h đư ợ c thêm vào cây từ
trái sang phả i
3/11/2010 www.lhu.edu.vn
Chư ơ ng
Chư ơ ng 6 C
6 Cấấu tr
u trú
úc cây
c cây
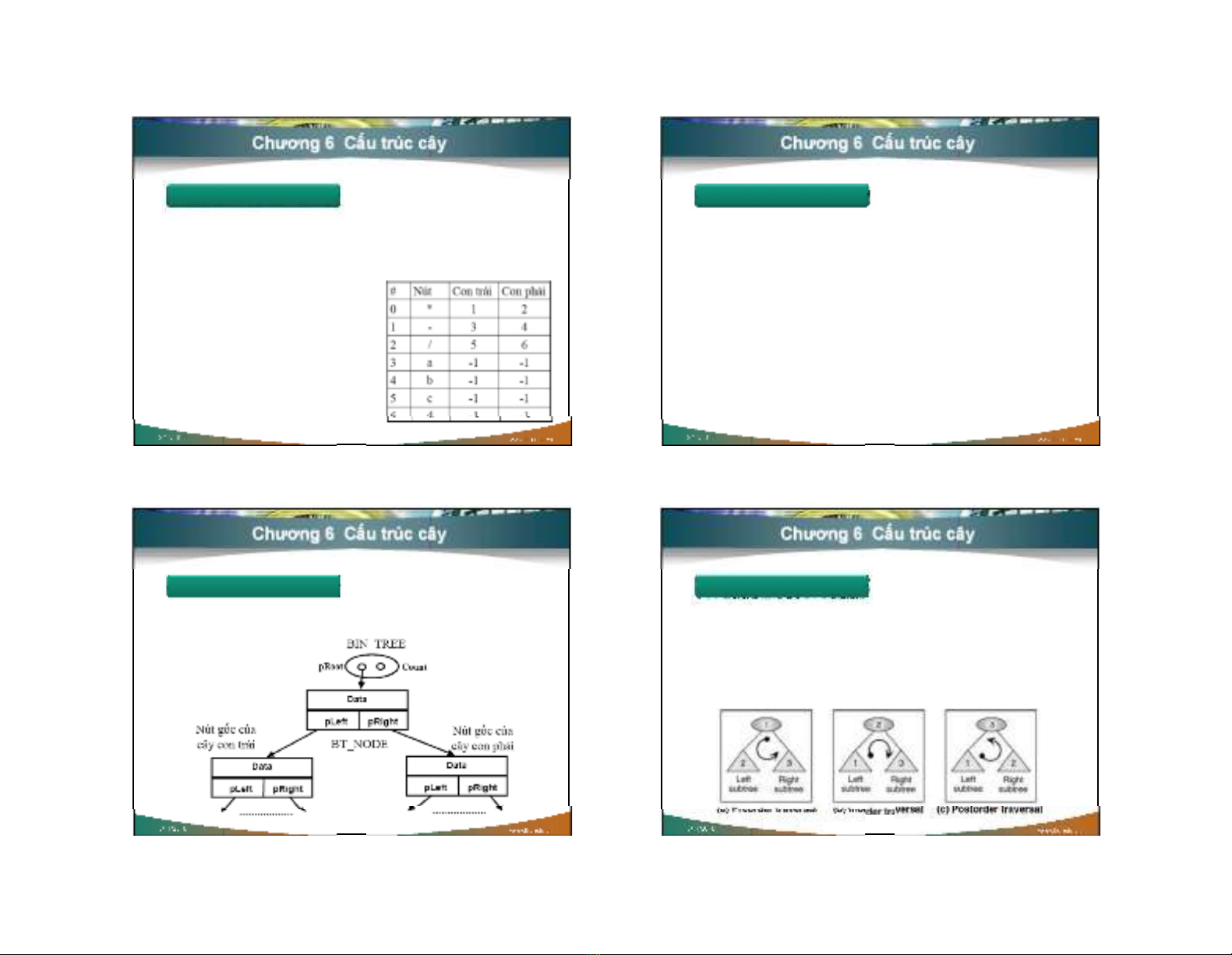
Cây nh
Cây nhịịphân
phân
Cây nhị phân là cây có bậ c = 2
Độ cao củ a cây nhị phân có N nút:
•hT(max) = N
•hT(min) = [logN] + 1
3/11/2010 www.lhu.edu.vn
Chư ơ ng
Chư ơ ng 6 C
6 Cấấu tr
u trú
úc cây
c cây
Cây nh
Cây nhịịphân
phân
Cấ u trúc lư u trữ dùng mả ng
Đị nh nghĩa các cấ u trúc dữ liệ u
typedef struct NODE
{
int Data;
int Left; // chỉ số nút con trái
int Right; // chỉ số nút con phả i
} NODETYPE; // cấ u trúc 1 node
// cây nhị phân có N nút
NODETYPE tree[N];
3/11/2010 www.lhu.edu.vn
Chư ơ ng
Chư ơ ng 6 C
6 Cấấu tr
u trú
úc cây
c cây
Cây nh
Cây nhịịphân
phân
Cấ u trúc lư u trữ dùng con trỏ
Đị nh nghĩa các cấ u trúc dữ liệ u
typedef struct NODE
{ int Data;
NODE *pLeft; // con trỏ đế n nút con trái
NODE *pRight; // con trỏ đế n nút con phả i
} NODETYPE; // binary tree node
typedef struct BIN_TREE
{ int Count; // Số nút trong cây
NODETYPE *pRoot; // con trỏ đế n nút gố c
}; // binary tree
3/11/2010 www.lhu.edu.vn
Chư ơ ng
Chư ơ ng 6 C
6 Cấấu tr
u trú
úc cây
c cây
Cây nh
Cây nhịịphân
phân
Cấ u trúc lư u trữ dùng con trỏ
3/11/2010 www.lhu.edu.vn
Chư ơ ng
Chư ơ ng 6 C
6 Cấấu tr
u trú
úc cây
c cây
Cây nh
Cây nhịịphân
phân
Có 3 cách duyệ t cây:
•Duyệ t gố c trư ớ c (Pre-Order) NLR
•Duyệ t gố c giữ a (In-Order) LNR
•Duyệ t gố c sau (Post-Order) LRN

![Tài liệu ôn tập Lý thuyết và Thực hành môn Tin học [mới nhất/chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251001/kimphuong1001/135x160/49521759302088.jpg)





![Tài liệu giảng dạy Chế bản điện tử nâng cao - Trường CĐ Kinh tế - Kỹ thuật Vinatex TP. HCM [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2022/20221108/runthenight01/135x160/6971667958229.jpg)


















