Ch
Ch ng 2ương 2ươ :
:
BI
BI U DI N TÍN HI U VÀ H TH NG R I R C Ể Ễ Ệ Ệ Ố Ờ Ạ
U DI N TÍN HI U VÀ H TH NG R I R C Ể Ễ Ệ Ệ Ố Ờ Ạ
TRONG MI N PH C ZỀ Ứ
TRONG MI N PH C ZỀ Ứ
2.1 BI N Đ IẾ Ổ Z
2.2 CÁC TÍNH CH T BI N Đ I Ấ Ế Ổ Z
2.3 BI N Đ I Z NG CẾ Ổ ƯỢ
2.4 BI U DI N H TH NG TRONG MI N ZỂ Ễ Ệ Ố Ề
•N u x(n) nhân qu thì : (*) (**)ế ả
•Ký hi u:ệ
x(n) X(z) hay X(z) = Z{x(n)}
X(z) x(n) hay x(n) = Z-
1{X(z)}
2.1 BI
2.1 BIẾ
ẾN
N Đ IỔ
Đ IỔ Z
Z
2.1.1
2.1.1 Đ NH NGHĨA BI N Đ IỊ Ế Ổ
Đ NH NGHĨA BI N Đ IỊ Ế Ổ Z:
Z:
∑
∞
=
−
=
0n
n
znxzX )()(
→←
Z
→←
−
1
Z
≡
Bi u th c (*) còn g i là bi n đ i Z hai phíaể ứ ọ ế ổ
•Bi n đ i Z c a dãyế ổ ủ x(n):
(*)
(**)
Trong đó Z – bi n s ph cế ố ứ
∑
∞
−∞=
−
=
n
n
znxzX )()(
•Mi n h i t c a bi n đ i Zề ộ ụ ủ ế ổ - ROC (Region Of
Convergence)
là t p h p t t c ậ ợ ấ ả các giá tr Z n m trong m t ph ng ph cị ằ ặ ẳ ứ sao
cho X(z) h i tộ ụ.
2.1.2 MI N H I T C A BI N Đ I Z (ROC)Ề Ộ Ụ Ủ Ế Ổ
2.1.2 MI N H I T C A BI N Đ I Z (ROC)Ề Ộ Ụ Ủ Ế Ổ
+++=
∑
∞
=
)2()1()0()(
0
xxxnx
n
1)(lim
1
<
∞→
n
n
nx
0
0
Im(Z)
Re(z)
Rx+
Rx-
ROC
•Để tìm ROC của X(z) ta áp
d ngụ
tiêu chu nẩ Cauchy
•Tiêu chu nẩ Cauchy:
M t chu i có d ngộ ỗ ạ :
h i t ộ ụ
n uế:
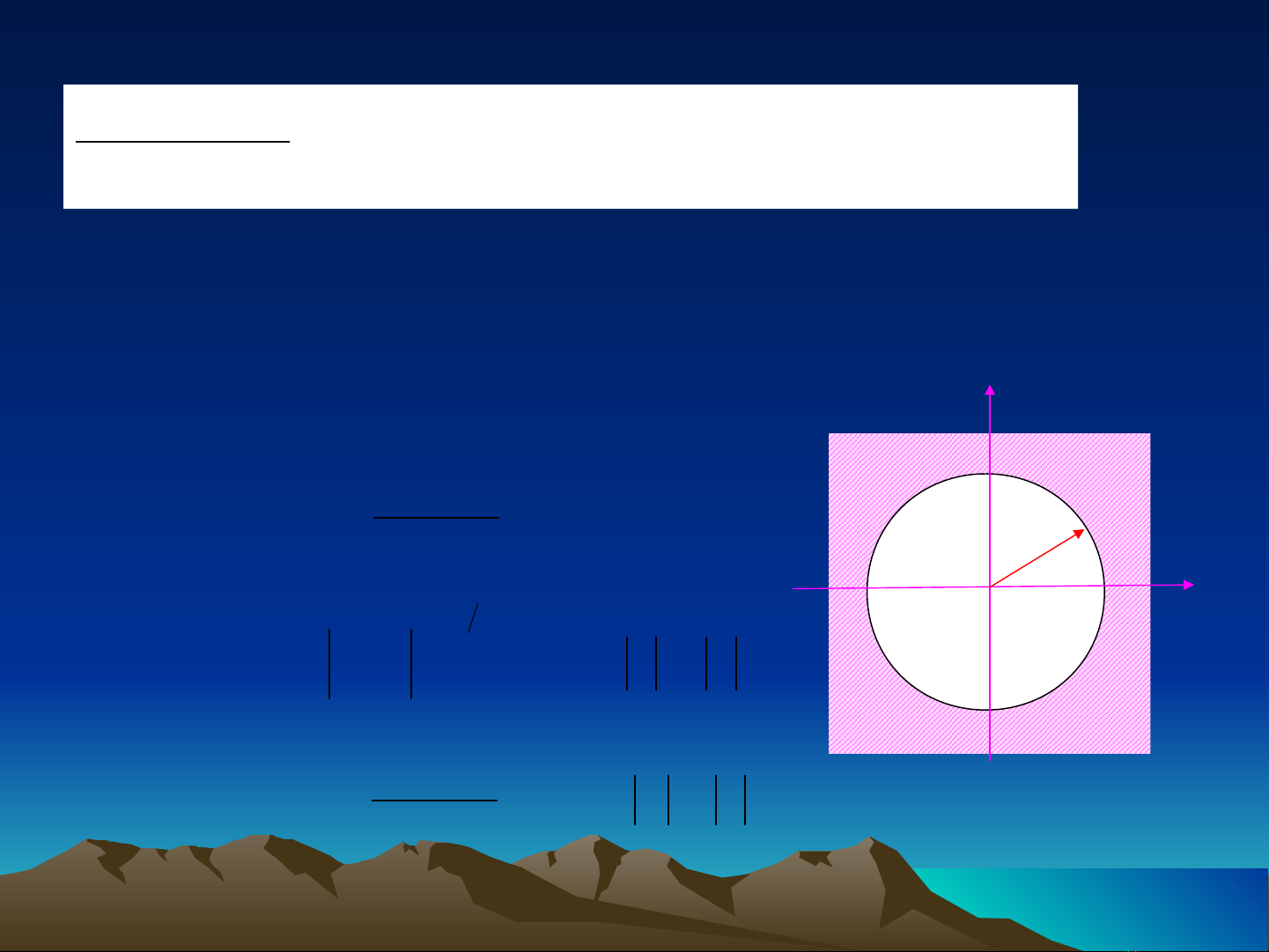
Ví d 2.1.1ụ: Tìm bi n đ i Z & ROC c a ế ổ ủ
x(n)=anu(n)
( )
n
n
az
∑
∞
=
−
=
0
1
1
1
1
−
−
=
az
)z(X
azazlim
n
n
n
>⇔<
−
∞→
1
1
1
∑
∞
−∞=
−
=
n
n
z)n(x)z(X
[ ]
∑
∞
−∞=
−
=
n
nn
z)n(ua
∑
∞
=
−
=
0n
nn z.a
0
ROC
ROC
Im(z)
Re(z)
/a/
Theo tiêu chuẩn Cauchy,
X(z) sẽ hội tụ:
N uế
:
V y:ậ
a;
az
)z(X
>
−
=
−
Z:ROC
1
1
1
( )
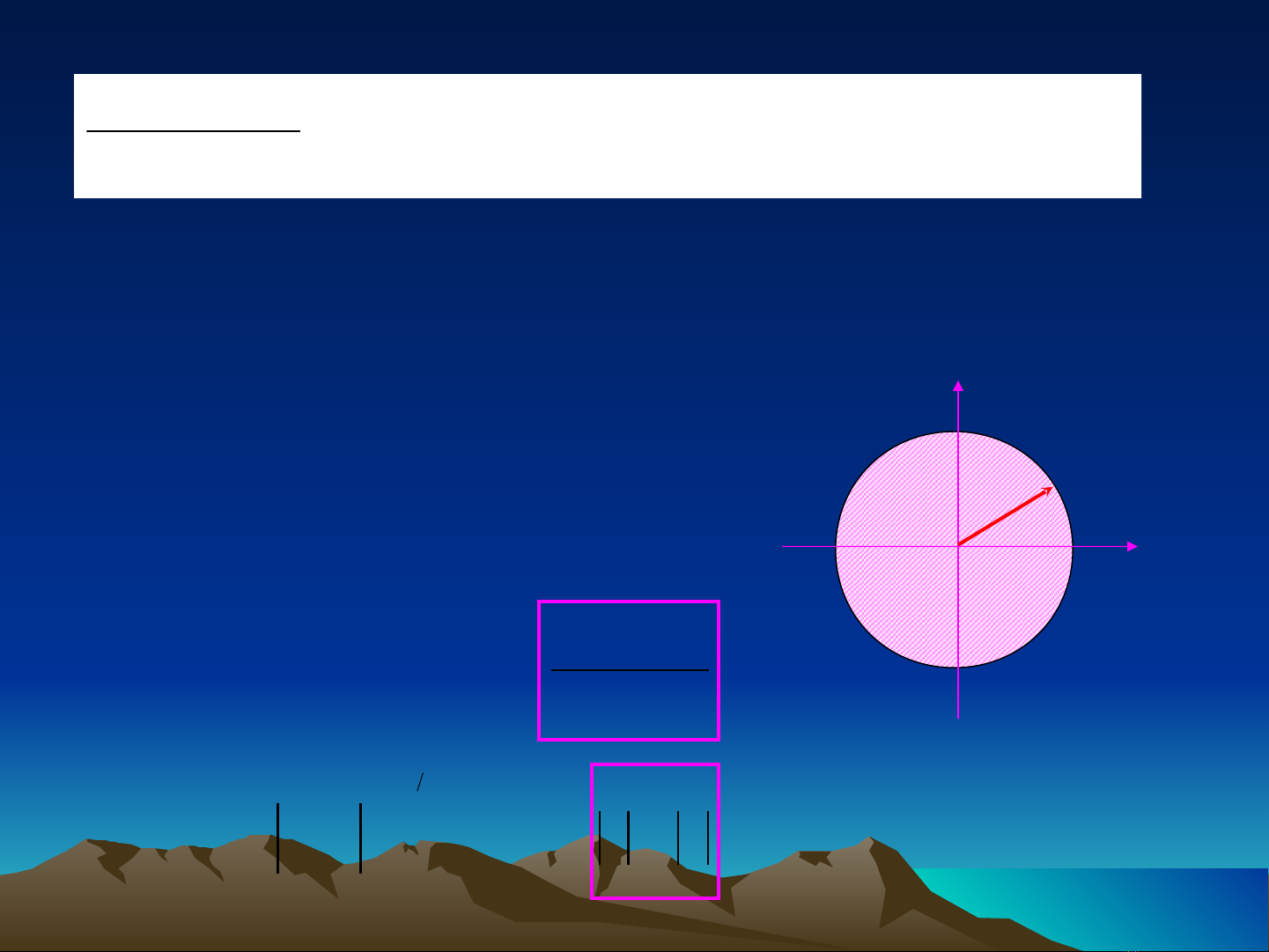
m
m
za
∑
∞
=
−
−=
1
1
azzalim
n
n
n<⇔<
−
∞→ 1
1
1
∑
∞
−∞=
−
=
n
n
z)n(x)z(X
[ ]
∑
∞
−∞=
−
−−−=
n
nn
z)n(ua 1
∑
−
−∞=
−
−=
1
n
nn
z.a
( )
1
0
1+−=
∑
∞
=
−
m
m
za
( )
1
0
1+−=
∑
∞
=
−
n
m
za)z(X
1
1
1
−
−
=
az
0
ROC
ROC
Im(z)
Re(z)
/a/
Theo tiêu chuẩn Cauchy,
X(z) sẽ hội tụ:
N uế
:
Ví d 2.1.2ụ: Tìm bi n đ i Z & ROC c a ế ổ ủ x(n)=-anu(-n-
1)