DANH MUÏC ÑAÀU TÖ DANH MUÏC ÑAÀU TÖ
HIEÄU QUAÛHIEÄU QUAÛ
ChChươươngng 66
1
HIEÄU QUAÛHIEÄU QUAÛ
nChuùng ta seõ taäp trung vaøo caâu traû lôøi cho caâu
hoûi sau: "Vôùi moät nhoùm caùc chöùng khoaùn coù
saün, baèng caùch naøo chuùng ta xaùc ñònh ñöôïc
caùch
keát
hôïp
toát
nhaát
caùc
chöùng
ñoù
vaøo
Lyù thuyeát DMÑT cuûa Markowitz
2
caùch
keát
hôïp
toát
nhaát
caùc
chöùng
ñoù
vaøo
caùc danh muïc ñaàu tö ?".
nKhi traû lôøi caâu hoûi naøy, chuùng ta seõ tìm nhöõng
danh muïc ñaàu tö maø ñöôïc döï kieán seõ taïo ra lôïi
nhuaän toái ña vôùi möùc ruûi ro töông öùng.
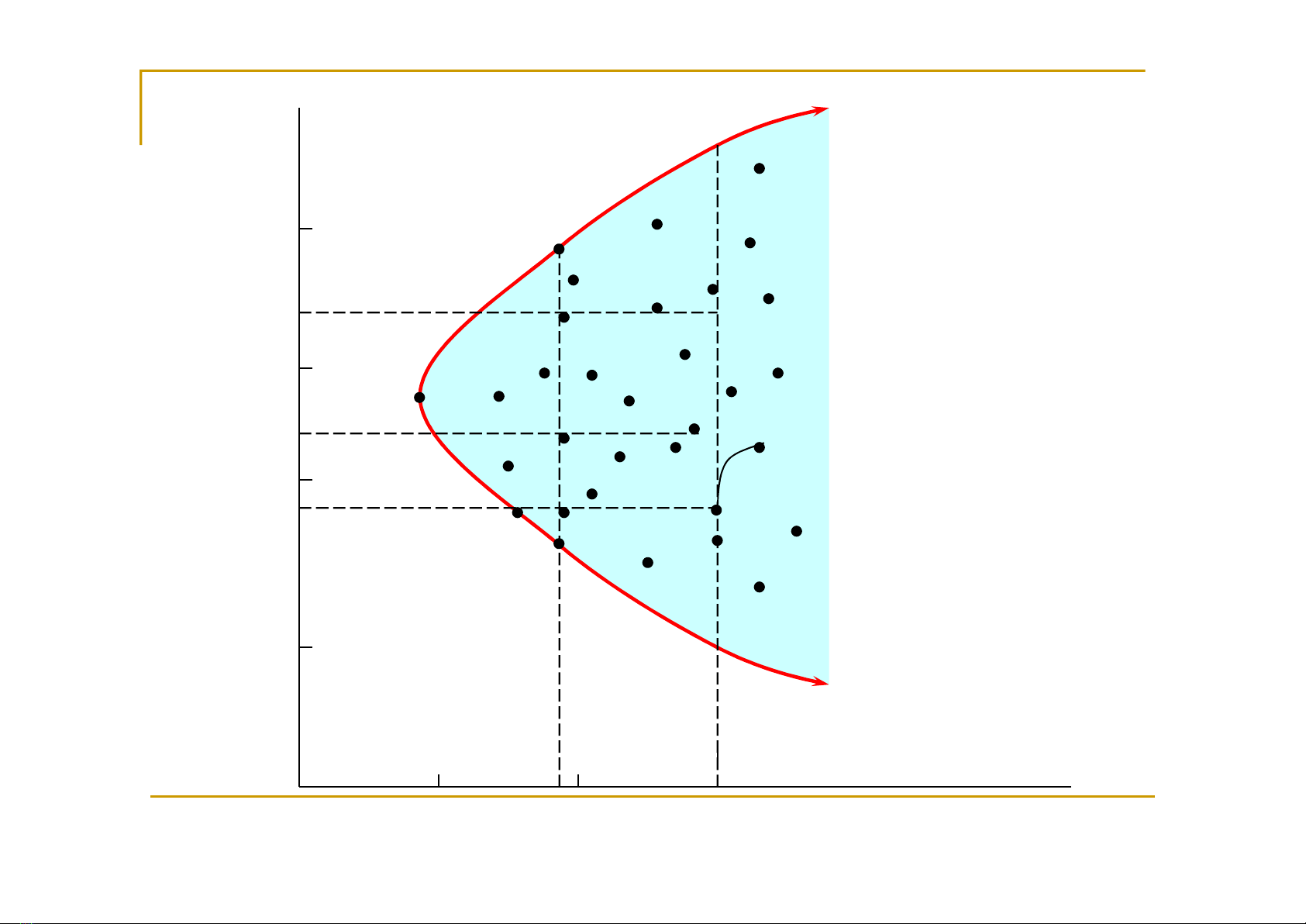
C
B
MVP
Laõi suaát öôùc tính (%)
20
E(rP)
15
10
3
Taäp hôïp bieán thieân toái thieåu
D
A
Ñoä leäch chuaån cuûa lôïi nhuaän (%)
F(rP)
15105
10
5
FE
nÑöôøng cong treân laø taäp hôïp bieán thieân toái thieåu, nghóa laø
caùc DM naèm treân ñöôøng cong naøy coù ruûi ro thaáp nhaát vôùi
möùc laõi suaát töông öùng. Vaäy :
DM bieán thieân toái thieåu laø caùc DM coù möùc lôïi nhuaän cho
tröôùc nhöng coù ruûi ro thaáp nhaát
E(r
)
= cont.
vaø
s
(r
)
=> Min
Lyù thuyeát DMÑT cuûa Markowitz
4
E(r
j
)
= cont.
vaø
s
(r
j
)
=> Min
nNöûa treân cuûa ñöôøng cong laø taäp hôïp hieäu quaû, nghóa laø caùc
DM naèm ôû nöûa treân ñöôøng cong laø caùc DM hieäu quaû. Vaäy:
DM hieäu quaû laø caùc DM vôùi moät möùc ruûi ro cho saün nhöng seõ
coù laõi suaát öôùc tính coù theå ñaït ñöôïc cao nhaát.
s(rA)= cont. vaø E(rA)=> Max
Taäp hôïp hieäu quaû vôùi baùn khoángTaäp hôïp hieäu quaû vôùi baùn khoáng
nChuùng ta seõ xaây döïng caùc DMÑT vôùi 3 CP :
E(rA) = 5% , E(rB) = 10% , E(rC) = 15%
nMa traän töông quan bieán thieân cuûa caùc coå phieáu :
A B C
A
25%
15%
17%
5
nTöø ma traän treân coù theå tính Ñoä leäch chuaån cuûa :
s(rA) = 50% , s(rB) = 46% , s(rC) = 53%
A
25%
15%
17%
B15% 21% 9%
C17% 9% 28%