1
Chương 8
BIẾN ĐỔI FOURIER RỜI RẠC VÀ BIẾN ĐỔI FOURIER NHANH
Trong chương 3 ta thấy chuỗi Fourier liên tục thời gian (CTFS) liên hệ thời gian liên tục với
tần số rời rạc, biến đổi Fourier liên tục thời gian (CTFT) liên hệ thời gian rời rạc với tần số rời rạc. Sự
biểu diễn hai hình thức Fourier trên là CTFS và CTFT, là không tuần hoàn trong miền tần số nhưng
hai phép biến đổi DTFS và DTFT thì toàn hoàn trong miền tần số đó là kết quả của sự lấy mẫu thời
gian.
Trong chương này, biến đổi Fourier rời rạc (DFT) và biến đổi Fourier nhanh được xét đến như
sự trình bày Fourier thứ ba mà áp dụng cho tín hiệu không tuần hoàn rời rạc thời gian có chu kỳ giới
hạn. DFT và FFT thì rất hữu ích trong sự phân tích và xử lý nhiều vấn đề của hệ thống và tín hiệu biến
biến thời gian LTI. Chúng cho phép xử lý bằng máy tính và vi xử lý tín hiệu số. Thật ra, DFT và FTT
đã được nói đến trong chương 3 (phần 3.9)
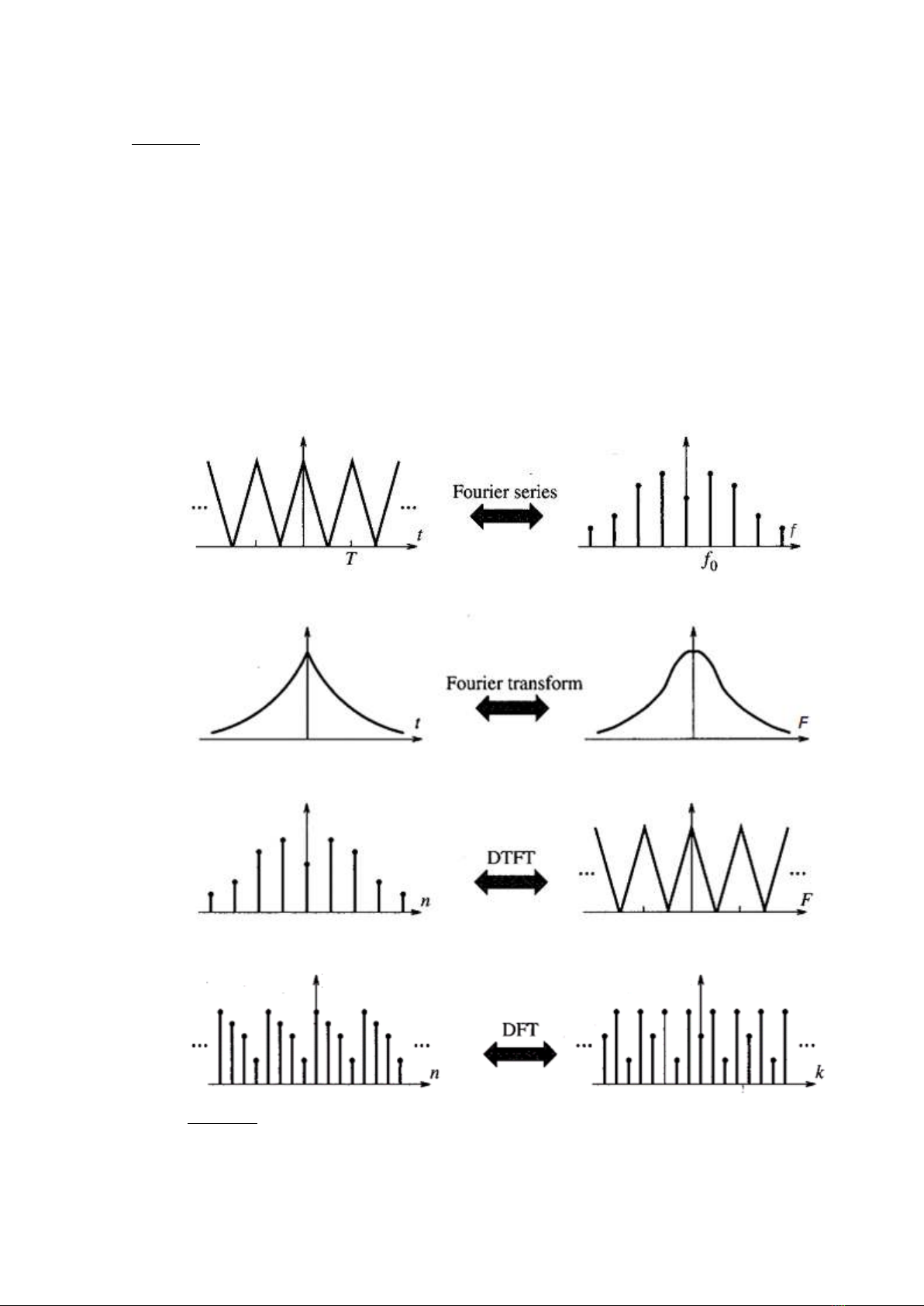
Hình 8.1: minh họa biến đổi thời gian-tần số cho sự phân tích Fourier khác nhau
8.1 BIẾN ĐỔI FOURIER RỜI RẠC (DFT)
Với tín hiệu không tần hoàn, x(n) nhìn chung nó tồn tại ở mọi thời điểm, biến đổi Fourier rời
rạc thời gian (DTFT) được định nghĩa (phần 3.5) như
Tín hiệu tương tự tuần hoàn
Phổ rời rạc không tuần hoàn
Tín hiệu tương tự không tuần hoàn
Phổ liên tục không tuần hoàn
Rời rạc và tuần hoàn
Rời rạc và tuần hoàn
Rời rạc và không tuần hoàn
Phổ liên tục tuần hoàn
spectrum
2

n
nj
enxX
)()(
(DFFT) (8.1)
Tín hiệu thời gian được phục hồi bằng cách lấy tích phân liên tục
(IDFT) (8.2)
Chú ý rằng tín hiệu thời gian x(n) thì rời rạc nhưng DFT của nó
)(
X
thì liên tục theo tần số, và cũng
giống như vậy với DTFT. Sự biến đổi áp dụng cho hệ thống là

n
nj
enhH
)()(
(Đáp ứng tần số) (8.3)
deHnh nj
2)(
2
1
)(
(Đáp ứng xung) (8.4)
8.1.1 Rời rạc tần số liên tục
Một số vấn đề của DTFT, đó là vấn đề của sự tính toán số (bằng máy tính hoặc vi xử lý số). Đầu tiên,
tổng vô hạn (8.1) và (8.3) không thể xử lý được, trong thực tế cả chuỗi x(n) cũng được giới hạn về
chiều dài hoặc cắt cụt đi, để giảm sự vô hạn của nó. Mặc khác frequency thì liên tục và theo nguyên
tắc ta phải tính (8.1) và (8.3) tại những giá trị vô hạn của dù tổng thì giới hạn về mặt thời gian. Vì
vậy tần số phải được rời rạc hóa. Thứ hai, như biến đổi
)(
X
và
)(
H
là những giá trị liên tục, vì
vậy ở đây vấn đề tính tích phân cần được xét đến. Điều này cũng dẫn đến sự cần thiết để rời răc hoặc
lấy mẫu tần .
Với tín hiệu không tuần hoàn x(n) và đáp ứng xung h(n), cách chúng ta lấy mẫu chúng? Càng
nhiều mẫu được lấy, những mẫu sẽ diễn tả tín hiệu tốt hơn nhưng lại tốn nhiều thời gian cho sự tính
toán. Trả lời cho câu hỏi quan trọng này nằm ở định lý lấy mẫu miền tần sô, đó là một dạng khác của
định lý lấy mẫu ở miền thời gian (phần 1.3.2). Định lý phát biểu như sau:
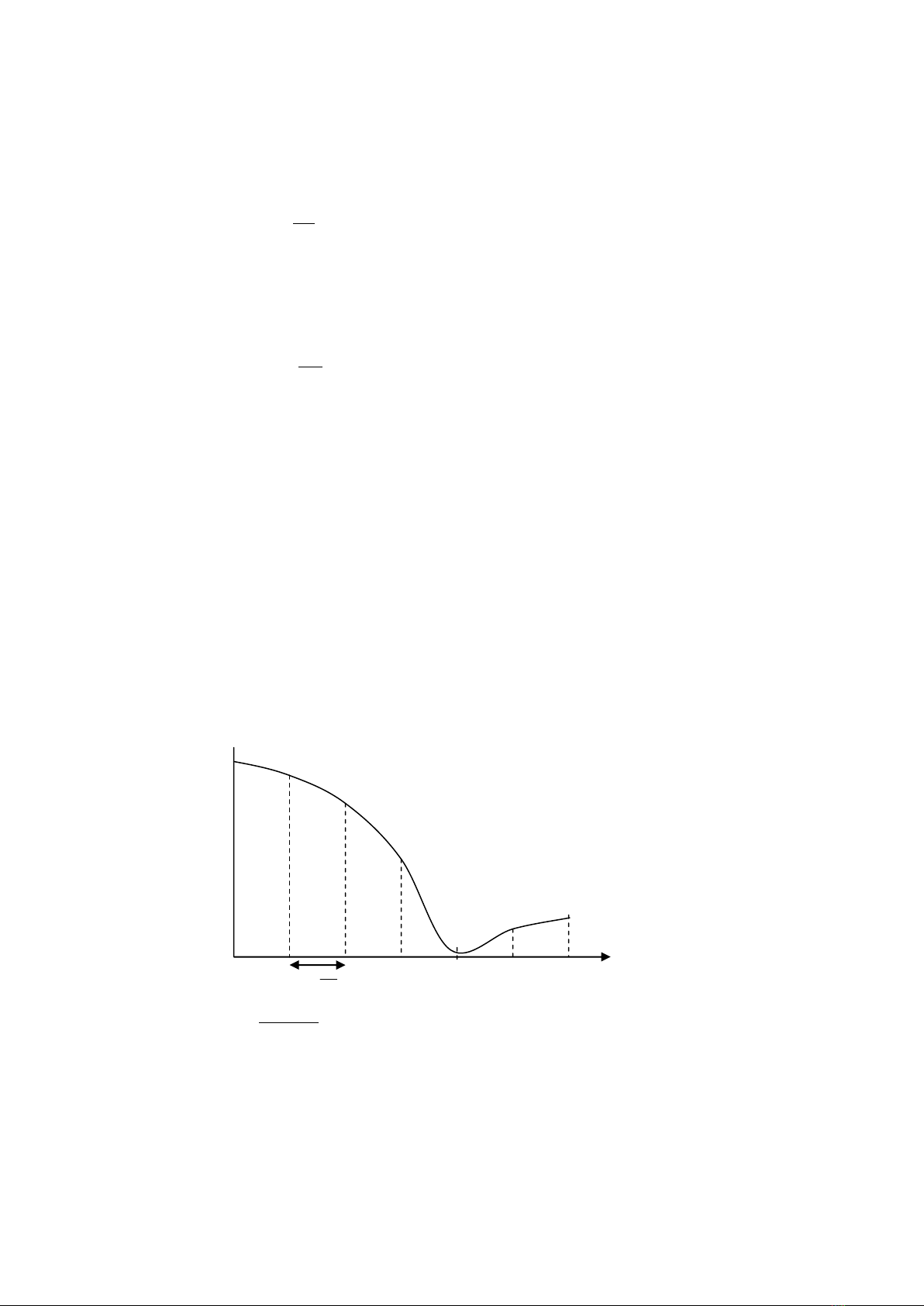
Phổ tần số liên tục của tín hiệu tồn tại trong một chu kỳ thời gian hữu hạn T0 giây có thẻ trình
bày một cách hoàn toàn bằng những mẫu tần số mà được lấy tại những khoảng tần số ít hơn 1/H0 Hz
(mẫu/giây). Phổ tần số có thể được phục hồi từ những mẫu tần số. (hình 8.2)
8.1.2 DFT và đảo của nó
Đầu tiên, biến đổi Fourier rời rạc (DFT) cũng như biến đổi Fourier rời rạc thời gian (DTFT) được lấy
mẫu tại những khoảng bằng nhau. Xét một tín hiệu nhân quả x(n) DTFT của nó có được từ (4.1) với
ngưỡng dưới của tổng là không.
)(
H
0
/2
0
1
H
Hình 8.2: Lấy mẫu đáp ứng tần số
3
0
)()(
n
nj
enxX
(8.5)
Kế đến xét một tín hiệu hữu hạn thời gian có N mẫu (từ n=0 đến n=N-1) thì biến đổi trên trở thành
1
0
)()(
N
n
nj
enxX
(8.6)
Bây giờ tính
)(
X
tại N giá trị rời rạc bằng nhau của trong chu kỳ 2:
1,...2,1,0,
2 Nkk
N
k
(8.7a)
Hoặc
2
k
k
k
fN

(8.7b)
và DFT của tín hiệu có N mẫu từ n = 0 đến n = N -1 là
)1(,...,2,1,0,)()(
1
0
)/2(
NkenxkX
N
n
knNj
(DFT) (8.8)
k được gọi là hệ số phổ và X(k) gọi là tần số lấy mẫu. Chuỗi x(n) có giá trị thực hoặc phức
Biến đổi ngược, tín hiệu x(n) được phục hồi như
)1(,...,2,1,0,)()( )/2(
1 NnekXnx knNj
N
(IDFT) (8.9)
Ta thấy DFT và IDFT thì giống như chuỗi Fourier rời rạc thời gian của x(n) tại chu kỳ N (phần 3.4).
Từ sự định nghĩa của DFT, ta dễ dàng thấy rằng X(0) là thực nếu x(n) thực.
DFT áp dụng cho hệ thống.
1,...,2,1,0,)()(
1
0
)/2(
NkenhkH
N
n
knNj
(DFT) (8.10)
1,...,2,1,0,)(
1
)(
1
0
)/2(
NnekH
N
nh
N
k
knNj
(IDFT) (8.11)
Sự định nghĩa ở (8.8), (8.9), (8.10) và (8.11) là DFT N điểm. Nếu ta tính X(k) từ (8.8) ở ngoài
dải
10 Nk
, ví dụ với
12 NkN
hoặc
012 kN
, ta sẽ thấy giá trị được lặp lại,
nghĩa là, X(k) tuần hoàn với chu kỳ N giống như vây, Nếu ta tính x(n) từ (8.9) ta sẽ thấy giá trị lập lại
nghĩa là x(n) tuần hoàn với chu kỳ N (tại thời điểm ban đầu ta xét x(n) là một chuỗi có chiều dài N từ
10 Nnton
). Vì vậy, hình 8.1 chỉ tín hiệu rời rạc và tuần hoàn được biến đổi DFT thành phổ
rời rạc và tuần hoàn.
Thường số N được lấy như là số nguyên mũ của 2 (đó là, 32, 64, 128…). Khi số mẫu x(n) không có
chiều dài như trên ta cộng thêm mẫu không để có chiều dài bằng với N (ví dụ nếu x(n) có 120 mẫu ta
sẽ cộng thêm 8 mẫu không để có 128 mẫu). Đây là thêm không hoặc padding không.
Để thuận tiện ta chú thích
)/( Nj
NeW
2
(8.12a)
Vì vậy
knNjkn
NeW )/(
2
(8.12b)
knNjkn
NeW )/(
2
(8.12c)
1
NN WW *
(8.12d)
Với dấu sao chú thích là liên hiệp phức. Cũng như vậy, thay vì viết (2 /N) biểu thức như trên ta cso
thể viết để rõ ràng hơn.
Ví dụ 8.1.1
Tìm DFT N điểm của tín hiệu
4
(a)
)()(
1nnx
(b)
1)(
2nx
(c)
Nnnnnx 003 0),()(
(d)
Nnnx n 0,2)(
4
(e)
Nnnnnnx 005 0),(4)(4)(
(f)
00006 )/2()1(0,cos)( kNandNnnnx
Giải
(a) Từ sự định nghĩa của DFT
1,...,1,0,11)()( 0)/2(
1
0
)/2(
1
NkeenkX kNj
N
n
knNj
(b) Từ sự định nghĩa của DFT
1
0
)/2(
21)(
N
n
knNj
ekX
Tổng có giá trị là N với k= 0, và 0 khi
0k
. Vì vậy
)()(
2kNkX
(c) Từ sự định nghĩa của DFT
1,...,1,01)()(
1
0
,)/2()/2(
)/2(
03
00
NkeeennkX
N
n
knNjknNj
knNj
(d) Từ sự định nghĩa của DFT
1
0
)/2(
1
0
)/2(
4)(
N
n
n
kNj
N
n
knNjn eekX
Sử dụng công thức chuỗi hình học hữu hạn( ), ta có
1,...,1,0,
1
1
)( )/2(
)/2(
4
Nk
e
e
kX kNj
N
kNj
(e) Chú ý rằng
)(
5nx
là xung chữ nhật số (thấy ) có độ rộng không mẫu.
Như trong (4.10a) và (4.10b), ta viết
)/2( Nj
NeW
knNjkn
N
knNjkn
NeWeW )/2()/2( ,
Vì vậy, từ định nghĩa của DFT và sử dụng công thức chuỗi hình học hữu hạn ( ), ta có
K
N
kn
N
n
n
kn
NW
W
WkX
1
1
)(
0
01
0
5
Tử số, lấy
2/
0
kn
N
W
làm thừa số chung, và mẫu số lấy
2/k
N
W
làm thừa số chung, biến đổi trên trở
thành
1,...,1,0,
)/sin(
)/sin(
)(
0
2/)1()/2((
2/2/
2/2/
2/)1(
5
0
00
0
Nk
Nk
Nkn
e
WW
WW
WkX
nkNj
k
N
k
N
kn
N
kn
N
nk
N
Ta có thể kiểm tra trường hợp
0
0n
(kết quả là 0) và trường hợp
1
0n
(kết quả như trong1
(b)).
(f) Diễn tả cosin trong thành phần của mũ phức.
00
2
1
2
1
0
cos)(
jnjn eennx
5
Vì vậy
nkj
N
n
nkj NN eekX )(
2
1
1
0
)(
2
10
2
0
2
)(
Với
00 )/2( kN
1
0
)(
2
1
1
0
)(
2
10
2
0
2
)(
N
n
nkkj
N
n
nkkj NN eekX
Tổng thứ nhất bằng không với
0
kk
, và bằng N với
0
kk
. Tổng thứ hai bằn không với
)( 0
kNk
, và bằng N với
)( 0
kNk
. Vì vậy biến đổi là
00
2
1,)( kNkandkkNkX
otherwise,0
Ta có thể hiểu
kN)/2(
là tần số DFT và viết
1,...,1,0,/
2 Nksampleradk
N
k
Nếu, đôi biến đổi có thể đặt trong dạng
1,...,1,0,)()(
1
0
NkenxX
W
n
nj
k
k
(DFT) (8.13)
1,...,1,0,)()(
1
0
1
NneXnx nj
N
k
k
N
k
(DFT) (8.14)
Vì vậy ta có thể tính
)( k
X
thay vì như thông thường X(k).
Ví dụ 8.1.2 (cũng thấy trong ví dụ 3.9.2)
(a) Tín đáp ứng tần số DFT
)( k
H
của một lọc FIR mà có đáp ứng xung là
h(0) = 0, h(1) = 1, h(2) = 2, h(3) = 3, otherwise h(n) = 0.
(b) Chứng mình rằng từ 4 giá trị của
)( k
H
đáp ứng xung có thể phục hồi một cách hoàn toàn
Giải
(a) Đáp ứng xung có 4 giá trị, vì vậy N = 4 và
4/2
k
. Cũng chú ý rằng dải
30 n
thì
h(n) = n. Đáp ứng tần số
)( k
H
là
3,2,1,0,)()()(
3
0
)2/(
3
0
)4/2(
4
2
kenhenhkH
n
knj
n
knj
Bây giờ
6321)0(,0
3
0
01)2/(
n
j
neHk
2232)(,1 2/32/
3
0
1)2/(
2jeeeneHk jjj
n
nj
2322)(,2 32
3
0
2)2/(
jjj
n
nj eeeeHk
22323)(,3 2/932/3
3
0
3)2/(
2
3jeeeeHk jjj
n
nj
Kết quả vẽ trong hình 8.3
H()
6
22
22
2