Chương 2:Các cổng logic cơ bản và đại số Boole

Ch

ng 2:Các c ng logic c b n

ươ

ơ ả

ổ và đ i s Boole ạ ố ằ

ạ ố

ế ả

ề

ạ ố

ng pháp bi u di n hàm Boole

ễ

2.1 Bi n và h ng trong đ i s boole 2.2 B ng chân tr ị 2.3 Các tiên đ và đ nh lý đ i s Boole ị 2.4 Các c ng logic c b n ơ ả ổ 2.5 Các ph ể ươ 2.6 T i thi u hóa hàm Boole ể ố 2.7 Bài t pậ

Chương 2: Các cổng logic cơ bản và đại số Boole

2.1 Bi n và h ng trong đ i s boole

ạ ố

ế

ằ

• Bi n và h ng:

ằ

ế – Bieán vaø haèng trong ñaïi soá Boole chæ nhaän moät

trong hai giaù trò laø 0 hoaëc 1

– Caùc giaù trò 0 vaø 1 khoâng phaûi laø caùc con soá

thöïc maø chæ bieåu dieãn moät möùc ñieän aùp, vaø chuùng ñöôïc goïi laø möùc logic.

– Ví duï: Trong maïch soá:

Möùc logic 0 ≈ möùc ñieän aùp töø 0V ñeán 0,8V. Möùc logic 1 ≈ möùc ñieän aùp töø 2V ñeán 5V.

ộ

NOT (

), (

• Các phép toán c b n ơ ả – C ng logic: OR ( + ) – Nhân logic: AND ( . ) , – L y bù: ) ấ

Chương 2: Các cổng logic cơ bản và đại số Boole

2.1 Bi n và h ng trong đ i s boole

ạ ố

ế

ằ

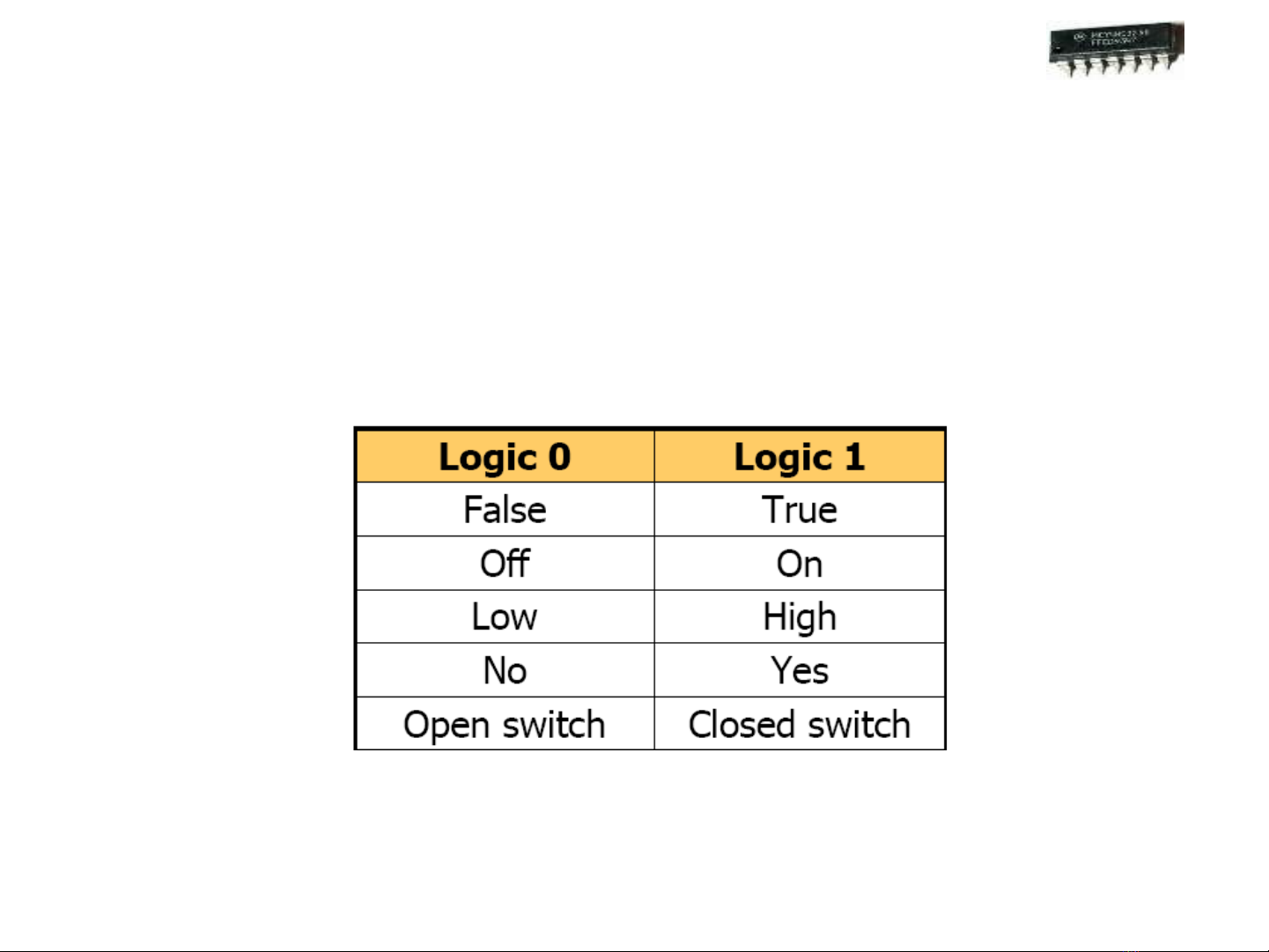
• Giá tr 0 và 1 trong đ i s Boole mang ý

ị nghĩa miêu t

các tr ng thái hay m c logic

ạ ố ạ

ả

ứ

Chương 2: Các cổng logic cơ bản và đại số Boole

ả

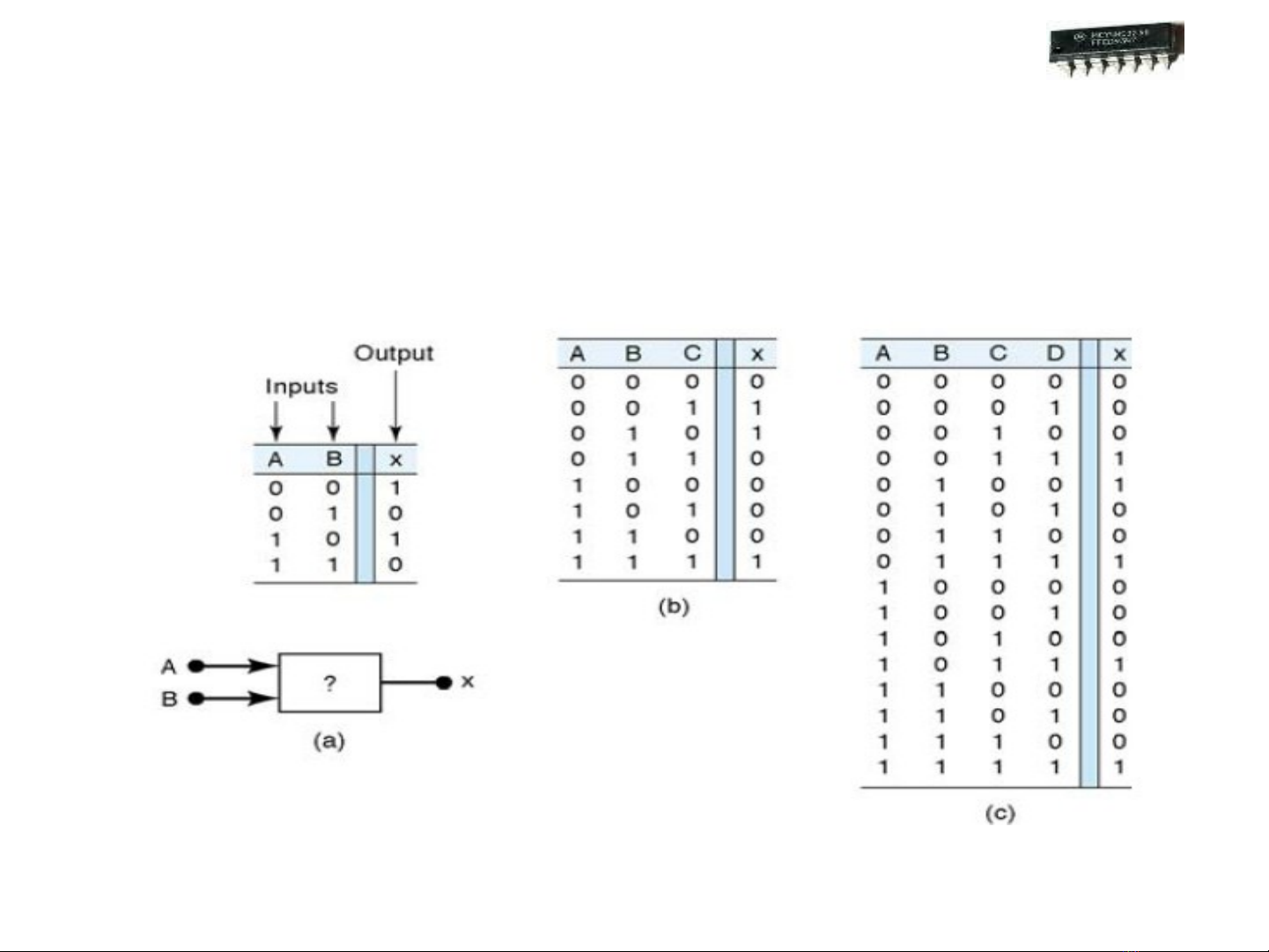
2.2 B ng chân tr (s th t) ị ự ậ m i quan h gi a các giá tr ngõ vào và ngõ ra

• Miêu t

ả ố

ệ ữ

ị

Chương 2: Các cổng logic cơ bản và đại số Boole

2.3 Các tiên đ và đ nh lý đ i s Boole ị

ạ ố

ề

• Tiên đề

ấ ả ế

t c k t qu thu c h nh phân ộ

ệ

ả

ị

– Tính kín: t – Giao hoán:

• x + y = y + x • x . y = y . x – Đ ng nh t ồ ấ • x + 0 = 0 + x = x • x . 1 = 1 . x = x

– Phân bố

• x + ( y . z ) = ( x + y ) . ( x + z ) • x . ( y + z ) = x . y + x . Z

– Bù:

Chương 2: Các cổng logic cơ bản và đại số Boole

2.3 Các tiên đ và đ nh lý đ i s Boole ị

ạ ố

ề

– Đ nh lý 1: ph đ nh hai lân

• Đinh lý ị

ủ ị

– Đ nh lý 2: đ ng nh t ấ

– Đ nh lý 3: qui t c gi a bi n và h ng

ế

ằ

ữ

– Đ nh lý 5: dán

– Đ nh lý 6: De Morgan

ị ồ • x + x = x • x . x = x ị ắ • x + 1 = 1 • x . 0 = 0 – Đ nh lý 4: nu t ị ố • x + x . y = x • x . (x + y) = x ị • x . ( x + y) = xy • x + ( x . y) = x + y ị • L • l

Chương 2: Các cổng logic cơ bản và đại số Boole

2.4 Các c ng logic c b n

ơ ả

ổ

Gi n đ th i gian ồ ờ

ả

• C ng NOT ổ Ký hi u:ệ

x t x x

• Chú ý: C ng NOT ch có m t ngõ vào

ộ

ổ

ỉ

x t

Chương 2: Các cổng logic cơ bản và đại số Boole

2.4 Các c ng logic c b n

ơ ả

ổ

• IC c ng NOT: 74LS04

ổ

Chương 2: Các cổng logic cơ bản và đại số Boole

2.4 Các c ng logic c b n

ơ ả

ổ

• C ng AND

ổ

x t

z = x y y t

z t

x y

z

ớ

V i AND có nhi u ngõ vào: ề -Ngõ ra s là 1 n u t ế ấ ả ẽ -Ngõ ra b ng 0 ch c n m t ngõ vào b ng 0 ộ ằ

t c ngõ vào là 1 ằ

ỉ ầ

0 0 0 1 1 0 1 1

0 0 0 1

Chương 2: Các cổng logic cơ bản và đại số Boole

2.4 Các c ng logic c b n

ơ ả

ổ

• IC c ng AND: 74LS08

ổ

Chương 2: Các cổng logic cơ bản và đại số Boole

2.4 Các c ng logic c b n

ơ ả

ổ

• C ng OR

ổ

x t

x y t

z = x +y y y z t

ề

ớ

x y

z

ằ

ế

ấ

t c ngõ vào

ế ấ ả

0 0 0 1 1 0 1 1

0 1 1 1

V i OR có nhi u ngõ vào: - Ngõ ra b ng 1 n u có ít nh t 1 ngõ vào b ng 1ằ - Ngõ ra b ng 0 n u t ằ b ng 0 ằ

Chương 2: Các cổng logic cơ bản và đại số Boole

2.4 Các c ng logic c b n

ơ ả

ổ

• IC c ng OR: 74LS32

ổ

Chương 2: Các cổng logic cơ bản và đại số Boole

2.4 Các c ng logic c b n

ơ ả

ổ

• IC c ng OR ổ

Chương 2: Các cổng logic cơ bản và đại số Boole

2.4 Các c ng logic c b n

ơ ả

ổ

• C ng NAND

ổ

x t

x z = x y y t y

z t

ớ

x y

z

ề ế

ằ

t c ngõ vào b ng 1

V i NAND có nhi u ngõ vào: - Ngõ ra b ng 1 n u có ít nh t 1 ngõ vào ấ b ng 0 -Ngõ ra b ng 0 n u t ằ

ế ấ ả

ằ

0 0 0 1 1 0 1 1

1 1 1 0

Chương 2: Các cổng logic cơ bản và đại số Boole

2.4 Các c ng logic c b n

ơ ả

ổ

• IC c ng NAND

ổ

Chương 2: Các cổng logic cơ bản và đại số Boole

2.4 Các c ng logic c b n

ơ ả

ổ

• C ng NOR

ổ

x t

x z = x + y y t y

z t

x y

z

ớ

ằ

ề ế

ằ

t c ngõ vào b ng 0

ế ấ ả

ằ

V i NOR có nhi u ngõ vào: Ngõ ra b ng 0 n u có ít nh t 1 ngõ vào ấ b ng 1 Ngõ ra b ng 1 n u t ằ

0 0 0 1 1 0 1 1

1 0 0 0

Chương 2: Các cổng logic cơ bản và đại số Boole

2.4 Các c ng logic c b n

ơ ả

ổ

• IC c ng NOR ổ

Chương 2: Các cổng logic cơ bản và đại số Boole

ơ ả

ổ

• C ng XOR (EXclusive _ OR )

2.4 Các c ng logic c b n ổ

z = x ¯ y y y

ớ

x y

z

ằ

t c ngõ vào b ng 0

ằ

ế ấ ả ề

ớ

0 0 0 1 1 0 1 1

0 1 1 0

ằ

ố ẻ

V i XOR có 2 ngõ vào: - Ngõ ra b ng 1 n u hai ngõ vào khác ế nhau -Ngõ ra b ng 0 n u t ằ V i XOR có nhi u ngõ vào: - Ngõ ra b ng 1 n u t ng s bit 1 là s l ố ế ổ

Chương 2: Các cổng logic cơ bản và đại số Boole

2.4 Các c ng logic c b n

ơ ả

ổ

• XNOR

x y

z

ớ

ế

ề

-V i XNOR có 2 ngõ vào, ngõ ra là 1 n u ngõ vào gi ng nhau ố -V i XNOR có nhi u ngõ vào, ngõ ra là 1 n u t ng bit 1 ngõ vào là s ch n

ớ ế ổ

ố ẵ

0 0 0 1 1 0 1 1

1 0 0 1

Chương 2: Các cổng logic cơ bản và đại số Boole

2.4 Các c ng logic c b n

ơ ả

ổ

• Dùng các c ng c b n bi u di n bi u th c sau

ơ ả

ứ

ể

ễ

ổ

X * 0 = ? X * 1 = X* X = X * X = X + 0 = X * 1 = X + X = X + X =

Chương 2: Các cổng logic cơ bản và đại số Boole

2.5 Các ph

ng pháp bi u di n hàm Boole

ươ

ể

ễ

Hàm boole có 2 d ng:ạ - Xác đ nh toàn ph n:t

i m i t

h p các bi n, hàm có giá tr c th (1 ho c 0),

ỗ ổ ợ

ầ ạ

ị

ị ụ ể

ế

ặ

VD1

ủ

ế

ầ

ị

ệ X, ta

ị có th gán t ể

- Xác đ nh không đ y đ : vài t h p bi n giá tr hàm không xác đ nh, ký hi u ổ ợ X b ng 0 ho c 1, VD2 t c tr ng thái ằ VD1: L p hàm 3 bi n, đ u ra b ng 1 n u s bit 1 nhi u h n bit 0 ề ằ ầ

ấ ả ạ ế

ặ ố

ế

ậ

ế

c phép thi, n u hoàn thành 1 trong

ế

VD2: L p cho phép thi. N u hoàn thành BT ậ và TN đ ượ 2 thì ch xét ờ

Chương 2: Các cổng logic cơ bản và đại số Boole

2.5 Các ph

ng pháp bi u di n hàm Boole

ươ

ễ

ể

ng pháp đ i s

2.5.1 B ng s th t ự ậ ả 2.5.2 Ph ươ

ạ ố

Chương 2: Các cổng logic cơ bản và đại số Boole

2.5 Các ph

ươ

ng pháp bi u di n hàm Boole ễ ể 2.5.1 B ng s th t ự ậ

ả

t kê t

t c các t

h p bi n, t

h p nào ch a xác đ nhký hi u X

ệ

ấ ả

ổ ợ

ế

ổ ợ

ệ

ị

VD1: L p hàm 3 bi n, đ u ra b ng 1 n u s bit 1 nhi u h n bit 0 ằ

ế

ề

ậ

ầ

ố

ế

c phép thi, n u hoàn thành 1 trong

ế

VD2: L p cho phép thi. N u hoàn thành BT ậ và TN đ ượ 2 thì ch xét ờ

u đi m:

Ư ể tr c quan, v i hàm nhi u bi n( >4), b ng r t dài

ự

ề

ế

ả

ấ

ớ

Chương 2: Các cổng logic cơ bản và đại số Boole

2.5 Các ph

ng pháp bi u di n hàm Boole

ể

ươ 2.5.2 Ph

ng pháp đ i s

ươ

ễ ạ ố

ừ

ố

t c ặ ấ ả

Có 2 d ng:ạ - Rút g n:ọ - Chu n t c: trong m i s h ng hay th a s có m t t ỗ ố ạ ẩ ắ ế

ủ

(Chu n t c tuy n

các bi n c a hàm: - T ng c a các tích ủ

ổ

ể -) CTT):là d ng t ng c a nhi u thành ph n mà m i thành ph n là tích c a đ y đ n bi n. ầ

ẩ ắ ỗ

ạ ầ

ủ ế

ổ ủ

ủ

ề

ầ

– Tích các t ngổ (Chu n t c h i

ẩ ắ

ủ

ề

ạ

ộ – CTH):là d ng tích c a nhi u thành ph n mà m i thành ph n là t ng c a đ y đ n bi n. ầ ầ

ủ

ế

ầ

ỗ

ổ

Chương 2: Các cổng logic cơ bản và đại số Boole

2.5 Các ph

ng pháp bi u di n hàm Boole

ể

ươ 2.5.2 Ph

ng pháp đ i s

ươ

ễ ạ ố

Chương 2: Các cổng logic cơ bản và đại số Boole

2.5 Các ph

ng pháp bi u di n hàm Boole

ể

ươ 2.5.2 Ph

ng pháp đ i s

ươ

ễ ạ ố

Chương 2: Các cổng logic cơ bản và đại số Boole

2.5 Các ph

ng pháp bi u di n hàm Boole

ươ 2.5.2 Ph

ễ ể ng pháp đ i s ạ ố

Chu n t c tuy n:

ươ ẩ ắ

ể

• Ví dụ

Chương 2: Các cổng logic cơ bản và đại số Boole

2.5 Các ph

ng pháp bi u di n hàm Boole

ươ 2.5.2 Ph

ễ ể ng pháp đ i s ạ ố

ươ ẩ ắ

ể

Chu n t c tuy n:

• Chú ý:

ỗ ố ạ

ệ

ọ

– M i s h ng g i minterm, ký hi u m

i, i=0,…,2n

ễ

1,x2) nh sau

– Có th bi u di n f(x ể ể • Nh phân ị

• Th p phân ậ

ổ

• T ng các minterm:

f(x1,x2) = m1 + m2 +m3

2.5 Các ph

ng pháp bi u di n hàm Boole

ươ 2.5.2 Ph

ươ

ễ ể ng pháp đ i s ạ ố chu n t c h i ộ ẩ ắ

• M i th a s trong chính t c h i g i ộ ọ

ừ

ố

ỗ

Maxterm, ký hi u Mệ

ắ i, i = 0,…2n

Ví d hàm 2 bi n ta có các maxterm:

ụ

ế

Chương 2: Các cổng logic cơ bản và đại số Boole

2.5 Các ph

ng pháp bi u di n hàm Boole

ươ 2.5.2 Ph

ươ

ễ ể ng pháp đ i s ạ ố chu n t c h i ộ ẩ ắ

• Ví dụ

t d ng chu n t c h i?

ế ạ

ẩ ắ

ộ

Chương 2: Các cổng logic cơ bản và đại số Boole

2.5 Các ph

ng pháp bi u di n hàm Boole

ng h p tùy đinh

ươ 2.5.2 Ph ươ Xét ví d có tr ụ

ễ ể ng pháp đ i s ạ ố ợ ườ

Bi u di n hàm f(A,B,C,D)

ể

ễ

Chương 2: Các cổng logic cơ bản và đại số Boole

2.6 Rút g n hàm Boole

ọ

ổ

ụ

ươ ng pháp đ i s

ể ế

ị

• Ph

• M c tiêu: S d ng ít c ng nh t ấ ử ụ • Có hai ph ng pháp • Ph ạ ố ươ – Dùng các tiên đ và đ nh lý đ bi n đ i ề ổ ng pháp Bìa Karnaugh ươ

Chương 2: Các cổng logic cơ bản và đại số Boole

2.6 Rút g n hàm Boole

ọ

ng pháp đ i s

ươ

ạ ố

• Ví d :ụ

Chương 2: Các cổng logic cơ bản và đại số Boole

ọ

2.6 Rút g n hàm Boole ng pháp Bìa Karnaugh Ph

ươ

ố

ộ

ư ả ể ể ệ

ệ ữ

ứ

ố

• Gi ng nh b ng chân tr , bìa Karnaugh là m t ị cách đ th hi n m i quan h gi a các m c logic ngõ vào và ngõ ra.

ng pháp đ

ượ

c s d ng ử ụ

ươ đ đ n gi n bi u th c logic.

• Bìa Karnaugh là m t ph ả

ể

• Ph

ng pháp

ộ ứ ng pháp này d th c hi n h n ph ễ ự

ệ

ươ

ể ơ ươ đ i s . ạ ố

ệ

ố

ớ ấ ng trình ch kh o sát s ỉ

ả

• Bìa Karnaugh có th th c hi n v i b t kỳ s ngõ ể ự vào nào, nh ng trong ch ố ươ ư ngõ vào nh h n 6. ỏ ơ

Chương 2: Các cổng logic cơ bản và đại số Boole

ọ

2.6 Rút g n hàm Boole ng pháp Bìa Karnaugh Ph

ươ

ng h p trong b ng chân tr t

ị ươ

ợ

ả

• Xây d ng BK ự – M i m t tr ộ ườ ớ

ứ

– Các ô trong bìa Karnaugh đ

ỗ ng v i 1 ô trong bìa Karnaugh ượ

c đánh s sao ố cho 2 ô k nhau ch khác nhau 1 giá tr . ị ỉ

ề

– Do các ô k nhau ch khác nhau 1 giá tr nên ỉ

ề

ị

ạ ể ạ

ơ ở ạ

ả

ầ

i đ t o m t ộ d ng t ng các ổ

chúng ta có th nhóm chúng l ể thành ph n đ n gi n h n ơ tích.

Chương 2: Các cổng logic cơ bản và đại số Boole

ọ

2.6 Rút g n hàm Boole ng pháp Bìa Karnaugh Ph

ươ

• Bìa hai bi nế

Vd:

F (A, B) = S (0, 2) + d(3) = P

(1) . D(3)

F

A

0 1

B

0 1

B

0 1

B

0 0 2 0 1 1 0

Bìa hai bi nế

Chu n t c tuy n

ẩ ắ

ể

Chu n h i tuy n ộ

ể

ẩ

1 1 3 1 X 1 0 X

Chương 2: Các cổng logic cơ bản và đại số Boole

ọ

2.6 Rút g n hàm Boole ng pháp Bìa Karnaugh Ph

ươ

Vd: F (A, B, C) = S (2, 4, 7) + d(0,1) = P

• Bìa 3 bi nế

(3, 5, 6) . D(0, 1)

F

AB

00 01 11 10

C

00 01 11 10

C

0 0 2 6 4 0 X 1 1

1 1 3 7 5 1 X 1

F

AB

00 01 11 10

C

0 X 0

1 X 0 0

Chương 2: Các cổng logic cơ bản và đại số Boole

2.6 Rút g n hàm Boole

ọ

ng pháp Bìa Karnaugh

ươ

• Bìa 4 bi nế

Vd:

F (A, B, C, D) = S (1, 3, 9, 11, 12, 13, 14, 15) + d(0, 4, 8)

F

AB

00 11 10 01

CD

00 01 11 10

CD

00 X X X 1 00 X X X

01 1 1 1 01 0

11 1 1 1 11 0

10 1 10 0 0 0

Chương 2: Các cổng logic cơ bản và đại số Boole

2.6 Rút g n hàm Boole

ọ

ng pháp Bìa Karnaugh

ươ

• Bìa 5 bi nế

A

F

0 1

BC

00 01 11 10 11 01 00 10

DE

00 12 8 28 20 16 24 0 4

01 13 9 25 29 21 17 1 5

11 15 11 27 31 23 19 3 7

10 14 10 26 30 22 18 2 6

Chương 2: Các cổng logic cơ bản và đại số Boole

2.6 Rút g n hàm Boole

ọ

ng pháp Bìa Karnaugh

ươ

• Nguyên t c nhóm

ắ

– Nhóm 2 ô “1” k nhau, lo i ra bi n xu t hi n

ệ ở

ấ

ạ

– Nhóm 4 ô “1” k nhau, lo i ra 2 bi n xu t hi n

ệ

ấ

ế ề c hai tr ng thái bù và không bù. ả ề

ạ

ở ả

ạ

– Nhóm 8 ô “1” k nhau, lo i ra 3 bi n xu t hi n

ề

ạ

ệ

ấ

ế c hai tr ng thái bù và không bù. ế c hai tr ng thái bù và không bù.

ạ

ở ả – …..

• Chú ý: ch nhóm 2, 4, 8, 16, 2

i k nhau

ỉ

ề

Chương 2: Các cổng logic cơ bản và đại số Boole

2.6 Rút g n hàm Boole

ọ

ng pháp Bìa Karnaugh

ươ

• Nhóm 2 ô (lo i 1 bi n) k c n ạ

ế ậ

ế

Chương 2: Các cổng logic cơ bản và đại số Boole

2.6 Rút g n hàm Boole

ọ

ng pháp Bìa Karnaugh

ươ

• Nhóm 4 ô (lo i 2 bi n) k c n ạ

ế ậ

ế

Chương 2: Các cổng logic cơ bản và đại số Boole

2.6 Rút g n hàm Boole

ọ

ng pháp Bìa Karnaugh

ươ

• Nhóm 4 ô (lo i 2 bi n) k c n ạ

ế ậ

ế

Chương 2: Các cổng logic cơ bản và đại số Boole

2.6 Rút g n hàm Boole

ọ

ng pháp Bìa Karnaugh

ươ

Chương 2: Các cổng logic cơ bản và đại số Boole

2.6 Rút g n hàm Boole

ọ

ng pháp Bìa Karnaugh

ươ

• n

Chương 2: Các cổng logic cơ bản và đại số Boole

2.6 Rút g n hàm Boole

ọ

ng pháp Bìa Karnaugh

ươ

• n

Chương 2: Các cổng logic cơ bản và đại số Boole

2.6 Rút g n hàm Boole

ọ

ng pháp Bìa Karnaugh

ươ

ọ ễ

ể

ị ằ

• Nguyên t c rút g n ắ – B c 1: Bi u di n hàm đã cho trên bìa Karnaugh. ướ – B c 2: Nhóm các ô có giá tr b ng 1 theo các quy ướ t c:ắ

ấ n (n nguyên).

ổ ổ

ề

c 2 cho đ n khi t

t c các ô

• T ng các ô là l n nh t. • T ng các ô ph i là 2 • Các ô này ph i n m k nhau – B c 3: ướ

ấ ả

ế

logic 1 đ u đ

ượ ị

ắ

ớ ả ả ằ Làm l i b ạ ướ c s d ng. ề ử ụ Xác đ nh k t qu theo các quy t c: ả ế ủ

ế

trên.

– B c 4: ướ • M i nhóm s là m t tích c a các bi n. ẽ ộ • K t qu là t ng c a các tích ủ ổ

ỗ ế

ả

ở

Chương 2: Các cổng logic cơ bản và đại số Boole

2.6 Rút g n hàm Boole

ọ

ng pháp Bìa Karnaugh

ươ

• Ví d : Rút g n bi u th c sau đây:

ứ

ụ

ể

ọ

Chương 2: Các cổng logic cơ bản và đại số Boole

2.6 Rút g n hàm Boole

ọ

ng pháp Bìa Karnaugh

ươ

• n

Chương 2: Các cổng logic cơ bản và đại số Boole

2.6 Rút g n hàm Boole

ọ

ng pháp Bìa Karnaugh

ươ

• Tr ng thái có tr

ng h p giá tr hàm không xác đ nh

ạ

ườ

ợ

ị

Chương 2: Các cổng logic cơ bản và đại số Boole

2.6 Rút g n hàm Boole

ọ

ng pháp Bìa Karnaugh

ươ • Rút g n hàm f: ọ