
11
∠Biên soạn: Ngô Đức Tài - H0889 971 004
NGÔ ĐỨC TÀI
SĐT: 0889 971 004
NGÔ ĐỨC TÀI
SĐT: 0889 971 004
SƯU TẦM VÀ BIÊN SOẠN
ππ
π
π
π
π
π
π
π
π
π
π
π
π
π
π
π
π
π
π
x
y
O
π
2
3π
2
π
2π
1
−1
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
CHƯƠNG 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
11
HỌC KÌ 1
ĐỒNG THÁP 2025

22 ∠Biên soạn: Ngô Đức Tài - H0889 971 004
MỤC LỤC
Chương I. Hàm số lượng giác và phương trình lượng giác 3
Chuyên đề 1. Góc lượng giác . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
Chuyên đề 2. Giá trị lượng giác của một góc lượng giác . . . . . . . . 18
Chuyên đề 3. Các công thức lượng giác . . . . . . . . . . . . . . . . . . . . 31
Chuyên đề 4. Hàm số lượng giác và đồ thị . . . . . . . . . . . . . . . . . . 46
Chuyên đề 5. Phương trình lượng giác cơ bản. . . . . . . . . . . . . . . . 61
Chuyên đề 6. Ôn tập chương 1 . . . . . . . . . . . . . . . . . . . . . . . . . . 81
33
∠Biên soạn: Ngô Đức Tài - H0889 971 004
1
Chương
HÀM SỐ LƯỢNG GIÁC VÀ
PHƯƠNG TRÌNH LƯỢNG
GIÁC
Mục lục của chương
Chuyên đề 1. Góc lượng giác ....................................3
Chuyên đề 2. Giá trị lượng giác của một góc lượng giác .........18
Chuyên đề 3. Các công thức lượng giác .........................31
Chuyên đề 4. Hàm số lượng giác và đồ thị ......................46
Chuyên đề 5. Phương trình lượng giác cơ bản ...................61
Chuyên đề 6. Ôn tập chương 1 .................................81
44 ∠Biên soạn: Ngô Đức Tài - H0889 971 004
11
C
h
u
y
ê
n
đ
ề
GÓC LƯỢNG GIÁC
I. GÓC LƯỢNG GIÁC
Khi xét chuyển động quay của một tia Om quanh góc O
của nó tính từ vị trí ban đầu Oa theo chiều cố định, người ta
quy ước chiều quay ngược ngược chiều kim đồng hồ là chiều
dương và chiều quay cùng chiều kim đồng hồ là chiều âm. Oa
m
+
−
Một vòng quay theo chiều dương tương ứng góc quay 360◦, một vòng quay theo chiều
âm tương ứng với góc quay −360◦. Khi tia Om quay:
•nửa vòng theo chiều dương, ta nói Om quay góc 1
2.360◦= 180◦.
•1
6vòng theo chiều dương, ta nói Om quay góc 1
6.360◦= 60◦.
•5
4vòng theo chiều âm, ta nói Om quay góc 5
4.(−360◦) = −450◦.
1) Khái niệm góc lượng giác
Cho hai tia Oa, Ob :
•Nếu một tia Om quay quanh gốc Ocủa nó theo một chiều cố định bắt đầu
từ vị trí tia Oa và dừng ở vị trí tia Ob thì ta nói tia Om quét một góc lượng
giác có tia đầu Oa, tia cuối Ob, kí hiệu (Oa, Ob) = α.
•Khi tia Om quay một góc α, ta nói số đo của góc lượng giác (Oa, Ob)bằng
α, kí hiệu sđ(Oa, Ob) = α.
Oa
b
m
+
Oa
b
m−
LƯU Ý. Với hai tia Oa và Ob cho trước, có vô số góc lượng giác tia đầu Oa và tia
cuối Ob. Ta dùng chung kí hiệu (Oa, Ob)cho tất cả các góc lượng giác này.
55
∠Biên soạn: Ngô Đức Tài - H0889 971 004
LChuyên đề 1. Góc lượng giác
Nhận xét: Số đo của các góc lượng giác có cùng tia đầu Oa và tia cuối Ob sai khác
nhau một bội nguyên của 360◦nên có công thức tổng quát là:
sđ(Oa, Ob) = α◦+k360◦(k∈Z),thường viết là (Oa, Ob) = α◦+k360◦
với α◦là số đo của một góc lượng giác bất kì có tia đầu Oa và tia cuối Ob.
KVí dụ 1KVí dụ 1 ⋆⋆⋆⋆⋆
Cho \
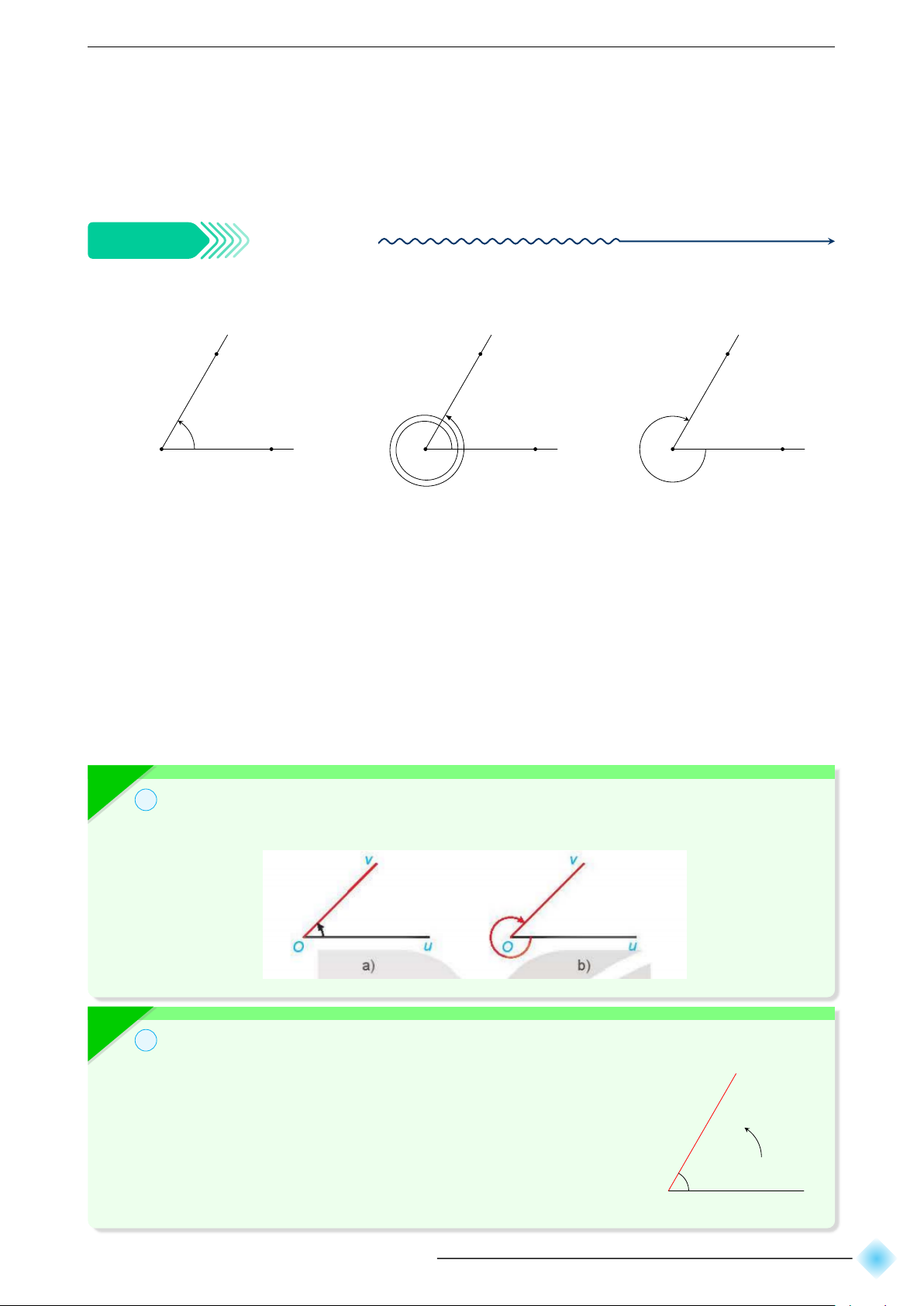
MON = 60◦. Xác định số đo của các góc lượng giác được biểu diễn trong hình bên
và viết công thức tổng quát của số đo góc lượng giác (OM, ON).
a) M
N
O
b) M
N
Oc) M
N
O
b
Hướng dẫn giải.
☞Số đo góc lượng giác (OM, ON)trong a) là 60°.
☞Số đo góc lượng giác (OM, ON)trong Hình b) là 60◦+ 2.360◦= 780◦.
☞Số đo góc lượng giác (OM, ON)trong Hình c) là 60°- 360°= -300°.
Công thức tổng quát là (OM, ON) = 60◦+k360◦(k∈Z).
L
L1Cho góc hình học uOv = 45◦. Xác định số đo của các góc lượng giác được biểu
diễn trong hình bên và viết công thức tổng quát của số đo góc lượng giác (Ou, Ov).
L
L2
Cho góc hình học uOv có số đo 60◦. Xác định số đo của góc
lượng giác (Ou,Ov) và (Ov,Ou).
u
v
+
60◦
O


























