Phương pháp tọa độ không gian: Chuyên đề hay nhất của Ngô Nguyên

CHUYÊN ĐỀ

PHƯƠNG PHÁP

TỌA ĐỘ KHÔNG GIAN

BIÊN SOẠN

TRẮC NGHIỆM HÌNH HỌC 12

Điện thoại: 0916.563.244

Website: TOANMATH.com

Mail: nhinguyenmath@gmail.com

Tài luyện thi TNQG năm 2017

CHUYÊN ĐỀ PHƯƠNG PHÁP TỌA ĐỘ KHÔNG GIAN TRẮC NGHIỆM TOÁN 12

NGÔ NGUYÊN – 0916.563.244

MỤC LỤC

TÓM TẮT LÍ THUYẾT ................................................................................................................................................................ 2

CÁC DẠNG BÀI TẬP .................................................................................................................................................................... 4

CHỦ ĐỀ 1. CÁC PHÉP TOÁN VỀ TỌA ĐỘ VÉC TƠ. XÁC ĐỊNH ĐIỂM – MỘT SỐ TÍNH CHẤT HÌNH HỌC

............................................................................................................................................................................................................. 4

I. PHƯƠNG PHÁP GIẢI VÀ BÀI TẬP CÓ HƯỚNG DẪN ....................................................................................... 4

II. BÀI TẬP TỰ LUYỆN ................................................................................................................................................ 4

CHỦ ĐỀ 2. PHƯƠNG TRÌNH MẶT CẦU ........................................................................................................................... 27

I. PHƯƠNG PHÁP GIẢI VÀ BÀI TẬP CÓ HƯỚNG DẪN ..................................................................................... 27

II. BÀI TẬP TỰ LUYỆN .............................................................................................................................................. 29

CHỦ ĐỀ 3. PHƯƠNG TRÌNH MẶT PHẲNG .................................................................................................................... 42

I. PHƯƠNG PHÁP GIẢI VÀ BÀI TẬP CÓ HƯỚNG DẪN ..................................................................................... 42

II. BÀI TẬP TỰ LUYỆN .............................................................................................................................................. 44

CHỦ ĐỀ 4. PHƯƠNG TRÌNH ĐƯỜNG THẲNG ............................................................................................................ 71

I. PHƯƠNG PHÁP GIẢI VÀ BÀI TẬP CÓ HƯỚNG DẪN ..................................................................................... 71

II. BÀI TẬP TỰ LUYỆN .............................................................................................................................................. 73

CHUYÊN ĐỀ PHƯƠNG PHÁP TỌA ĐỘ KHÔNG GIAN TRẮC NGHIỆM TOÁN 12

NGÔ NGUYÊN – 0916.563.244

TÓM TẮT LÍ THUYẾT

TỔNG HỢP MỘT SỐ CÔNG THỨC PHƯƠNG PHÁP TỌA ĐỘ KHÔNG GIAN

Trong không gian Oxyz cho:

   

; ; , ; ;

A A A B B B

A x y z B x y z

và

   

1 2 3 1 2 3

; ; , ; ;a a a a b b b b

. Khi đó:



 

;;

B A B A B A

AB x x y y z z   



     

2 2 2

B A B A B A

AB x x y y z z     



 

1 1 2 2 3 3

;;a b a b a b a b    



 

1 2 3

k.a ; ;ka ka ka



222

1 2 3

aaaa  



1 1 2 2 3 3

a ; ;b a b a b a b    



1 1 2 2 3 3

a. . . .b a b a b a b  



1 2 3

a / / . , 0 a

b a k b a b b b b



      





1 1 2 2 3 3

a . 0 . . . 0b a b a b a b a b      



2 3 3 1 12

a, ; ;

a a a a aa

bb b b b bb













,,abc

đồng phẳng

,:m n a mb nc    

hay

, . 0a b c









,,abc

không đồng phẳng

,:m n a mb nc    

hay

, . 0a b c







M chia đoạn AB theo tỉ số

1 ; ;

1 1 1

A B A B A B

x kx y ky z kz

k MA kMB M k k k

  



    

  



Đặc biệt: M là trung điểm AB:

;;

2 2 2

A B A B A B

x x y y z z

M  







G là trọng tâm tam giác ABC:

;;

3 3 3

A B C A B C A B C

x x x y y y z z z

G     







G là trọng tâm tứ diện ABCD:

;;

4 4 4

A B C D A B C D A B C D

x x x x y y y y z z z z

G        







Véctơ đơn vị:

(1;0;0); (0;1;0); (0;0;1)i j k  

Điểm trên các trục tọa độ:

( ;0;0) ; (0; ;0) ; (0;0; )M x Ox N y Oy K z Oz  

Điểm thuộc các mặt phẳng tọa độ:

     

( ; ;0) ; (0; ; ) ; ( ;0; )M x y Oxy N y z Oyz K x z Oxz  

Diện tích tam giác ABC:

ABC

S AB AC





Diện tích hình bình hành ABCD:

ABCD

S AB AC





Thể tích khối tứ diện ABCD:

1,.

ABCD

V AB AC AD





Thể tích khối hộp

. ' ' ' 'ABCD A B C D

. ' ' ' ' , . '

ABCD A B C D

V AB AD AA





 

u x y z u xi y j zk;;    

CHUYÊN ĐỀ PHƯƠNG PHÁP TỌA ĐỘ KHÔNG GIAN TRẮC NGHIỆM TOÁN 12

NGÔ NGUYÊN – 0916.563.244

Phương trình mặt cầu

Mặt cầu (S) tâm I(a;b;c) bán kính R có phương trình:

2 2 2 2

( ) ( ) ( )x a y b z c R     

Pt :

2 2 2 2 2 2

2 2 2 0 , a 0x y z ax by cz d b c d          

là phương trình của một mặt cầu .Mặt cầu

này có tâm I(a;b;c) và bán kính

2 2 2

R= a b c d  

Phương trình mặt phẳng: mp(P) qua điểm

0 0 0

( ; ; )M x y z

có VTPT

( ; ; )n a b c

có phương trình:

0 0 0

( ) ( ) ( ) 0a x x b y y c z z

     

Vị trí tương đối giữa hai mặt phẳng:

Cho hai mặt phẳng (P):Ax+By+Cz+D=0&(P):A’x+B’y+C’z+D’=0 với A’B’C’#0

(P) cắt (Q)

: : ': ': 'A B C A B C

(P) //(Q)

' ' ' '

A B C D

   

(P)



(Q)

' ' ' '

A B C D

   



( ) ( ) . ' . ' . ' 0P Q A A B B C C    

Khoảng cách và góc

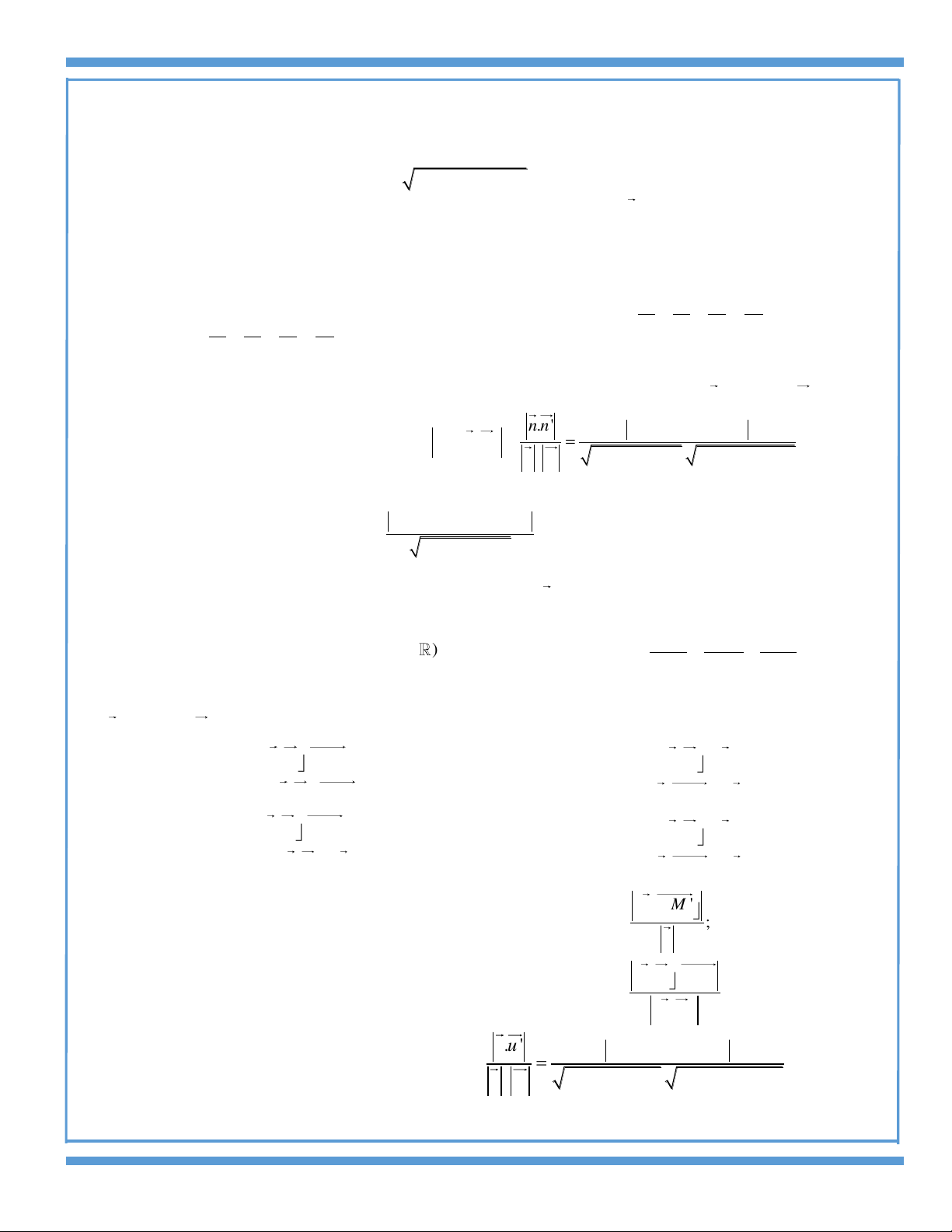
Góc giữa hai mp: Cho hai mp (P)&(Q) có hai vecto pháp tuyến lầ n lượt là

( ; ; ) & '( '; '; ')n A B C n A B C

.Gọi



là góc giữa hai mp.khi đó:

 

2 2 2 '2 2 2

.' . ' . ' . '

os os , ' .' . ' '

nn A A B B C C

c c n n

nn A B C A B C





      

Khoảng cách từ một điểm đến một mp: Khoảng cách từ điểm

 

0 0 0

;;M x y z

đến mp

(P):Ax+By+Cz+D=0 là:

0 0 0

2 2 2

d( ;( )) By Cz D

A B C

  



Phương trình đường thẳng trong không gian

Đường thẳng d qua điểm

 

0 0 0

;;M x y z

có vecto chỉphương

( ; ; )u a b c

thì:

Phương trình tham số :

()

x x at

y y bt t

z z ct





  







; Phương trình chính tắc:

0 0 0 ; a.b.c 0

x x y y z z

a b c

  

  

Vị trí tương đối của hai đường thẳng: Cho đường thẳng d&d’có các vecto chỉ phương

( ; ; ) & '( '; '; ')u A B C u A B C

và qua hai điểm M(x,y,z)&M(x’;y’;z’) khi đó:

d &d’ chéo nhau

, ' . ' 0u u MM







d &d’ đồng phẳng

, ' . ' 0u u MM







d &d’ cắt nhau

, ' . ' 0

, ' 0

u u MM

 

 









d &d’ song song

, ' 0

u MM





  









d &d’ trùng nhau

, ' 0

u MM





  









Khoảng cách từ một điểm M đến một đường thẳng d:

d( , ) ; ( ' )

u MM

M d M d







khoảng cách giữa hai đường thẳng chéo nhau d & d’:

 

, ' . '

d , '

u u MM









Góc giữa hai đường thẳng d & d’:

 

2 2 2 2 2 2

.' AA ' ' '

os , ' .' . ' ' '

uu BB CC

uu A B C A B C



       

CHUYÊN ĐỀ PHƯƠNG PHÁP TỌA ĐỘ KHÔNG GIAN TRẮC NGHIỆM TOÁN 12

NGÔ NGUYÊN – 0916.563.244

CÁC DẠNG BÀI TẬP

CHỦ ĐỀ 1. CÁC PHÉP TOÁN VỀ TỌA ĐỘ VÉC TƠ. XÁC ĐỊNH ĐIỂM – MỘT SỐ TÍNH CHẤT

HÌNH HỌC

I. PHƯƠNG PHÁP GIẢI VÀ BÀI TẬP CÓ HƯỚNG DẪN

Phương pháp:

Dạng 1: Chứng minh A, B, C là ba đỉnh tam giác

A,B,C là ba đỉnh tam giác

,AB AC

không cùng phương hay

,0AB AC









 

;;

G G G

G x y z

là trọng tâm tam giác ABC thì:

;;

3 3 3

A B C A B C A B C

G G G

x x x y y y z z z

x y z

     

  



ABC

S AB AC





. Suy ra diện tích của hình bình hành ABCD là:

ABCD

S AB AC





Đường cao:

2. ABC

AH BC





Dạng 2: Tìm D sao cho ABCD là hình bình hành

Chứng minh A, B, C không thẳng hàng

ABCD là hình bình hành

AB DC

Dạng 3: Chứng minh ABCD là một tứ diện:



;;AB AC AD

không đồng phẳng hay

; . 0AB AC AD









 

;;

G G G

G x y z

là trọng tâm tứ diện ABCD thì:

;;

4 4 4

A B C D A B C D A B C D

G G G

x x x x y y y y z z z z

x y z

        

  

Thể tích khối tứ diện ABCD:

1;.

ABCD

V AB AC AD





Đường cao AH của tứ diện ABCD:

3BCD

BCD

V S AH AH S

  

Thể tích hình hộp:

. ' ' ' ' ; . '

ABCD A B C D

V AB AD AA





II. BÀI TẬP TỰ LUYỆN

Câu 1. Cho 3 điểm A(2; 1; 4), B(–2; 2; –6), C(6; 0; –1). Tích

.AB AC

bằng:

A. –67 B. 65 C. 67 D. 33

Chuyên đề Phương pháp tọa độ không gian - Ngô Nguyên

Nhằm phục vụ quá trình học tập, giảng dạy của giáo viên và học sinh Chuyên đề Phương pháp tọa độ không gian do Ngô Nguyên biên soạn sẽ là tư liệu ôn tập hữu ích, giúp các bạn hệ thống lại kiến thức đã học.

Chủ đề:

Tài liệu liên quan

Tài liêu mới

AI tóm tắt

Giới thiệu tài liệu

Đối tượng sử dụng

Từ khoá chính

Nội dung tóm tắt

Hỗ trợ

Phương thức thanh toán

Theo dõi chúng tôi