Chuyên đ: PH NG TÍCH – TR C ĐNG PH NGề ƯƠ Ụ Ẳ ƯƠ
THPT Chuyên Nguy n T t Thành – Yên Báiễ ấ
I. Ph ng tích c a m t đi m đi v i đng tròn ươ ủ ộ ể ố ớ ườ
1. Đnh lý 1.1ị Cho đng tròn (O; R) và đi m M c đnh, OM = ườ ể ố ị d. M tộ
đng th ng thay đi qua M c t đng tròn t i hai đi m A và B. Khi đóườ ẳ ổ ắ ườ ạ ể
2 2 2 2
.MA MB MO R d R
= − = −
2.Đnh nghĩa.ị Giá tr không đi ị ổ
2 2
.MA MB d R
= −
trong đnh lý 1.1 đcị ượ
g i là ọph ng tíchươ c a đi m M đi v i đng tròn (O) và kí hi u ủ ể ố ớ ườ ệ
/(O)M
.
Ta có:
( )
2 2
/
.
M O
MA MB d R= = −�
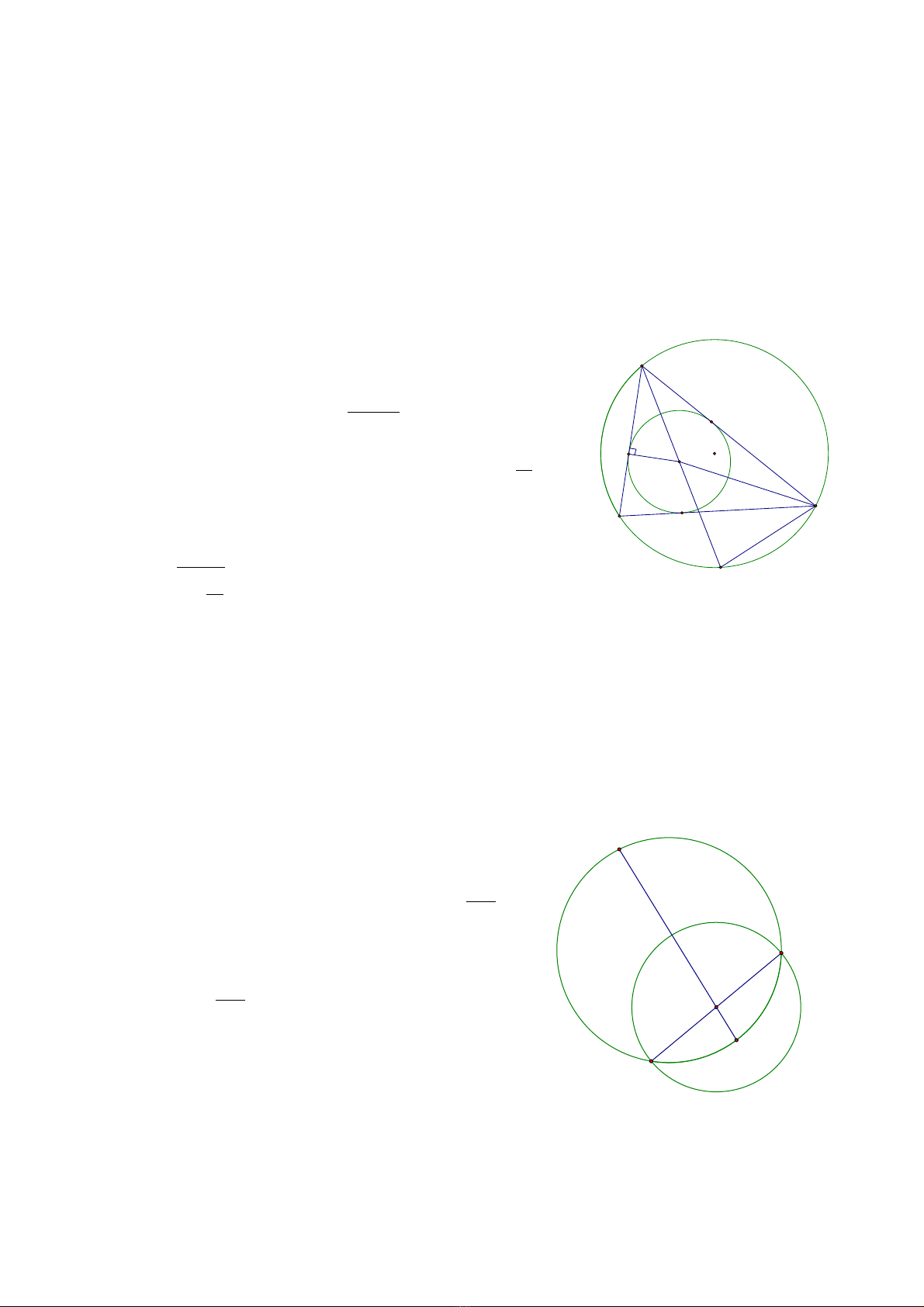
3.Đnh lý 1.2ị N u hai đng th ng AB và CD c t nhau t i P vàế ườ ẳ ắ ạ
. .PA PB PC PD
=
thì 4 đi m A, B, C, D cùng thu c m t đng tròn. ể ộ ộ ườ
Ch ng minh.ứ Gi s đng tròn ngo i ti p tam giác ABC c t CD t iả ử ườ ạ ế ắ ạ
D’. Khi đó ta có theo đnh lý 1.1 ta có ị
. .PA PB PC PD
=
, suy ra
. .PC PD PC PD D D
=
. Suy ra 4 đi m A, B, C và D cùng thu c m tể ộ ộ
đng tròn. ườ
4.Chú ý:
1. Khi M n m trên (O) thì ằ
( )
/
0
M O
=�
2. Khi M n m ngoài đng tròn (O) và MT là ti p tuy n c a (O) thìằ ườ ế ế ủ
3. N u A, B c đnh và ế ố ị
.AB AM const
=
M c đnh. Ý t ng này giúpố ị ưở
ta gi i các bài toán v đng đi qua đi m c đnh. ả ề ườ ể ố ị
II. Tr c đng ph ng c a hai đng tròn – Tâm đng ph ngụ ẳ ươ ủ ườ ẳ ươ
1. Tr c đng ph ngụ ẳ ươ
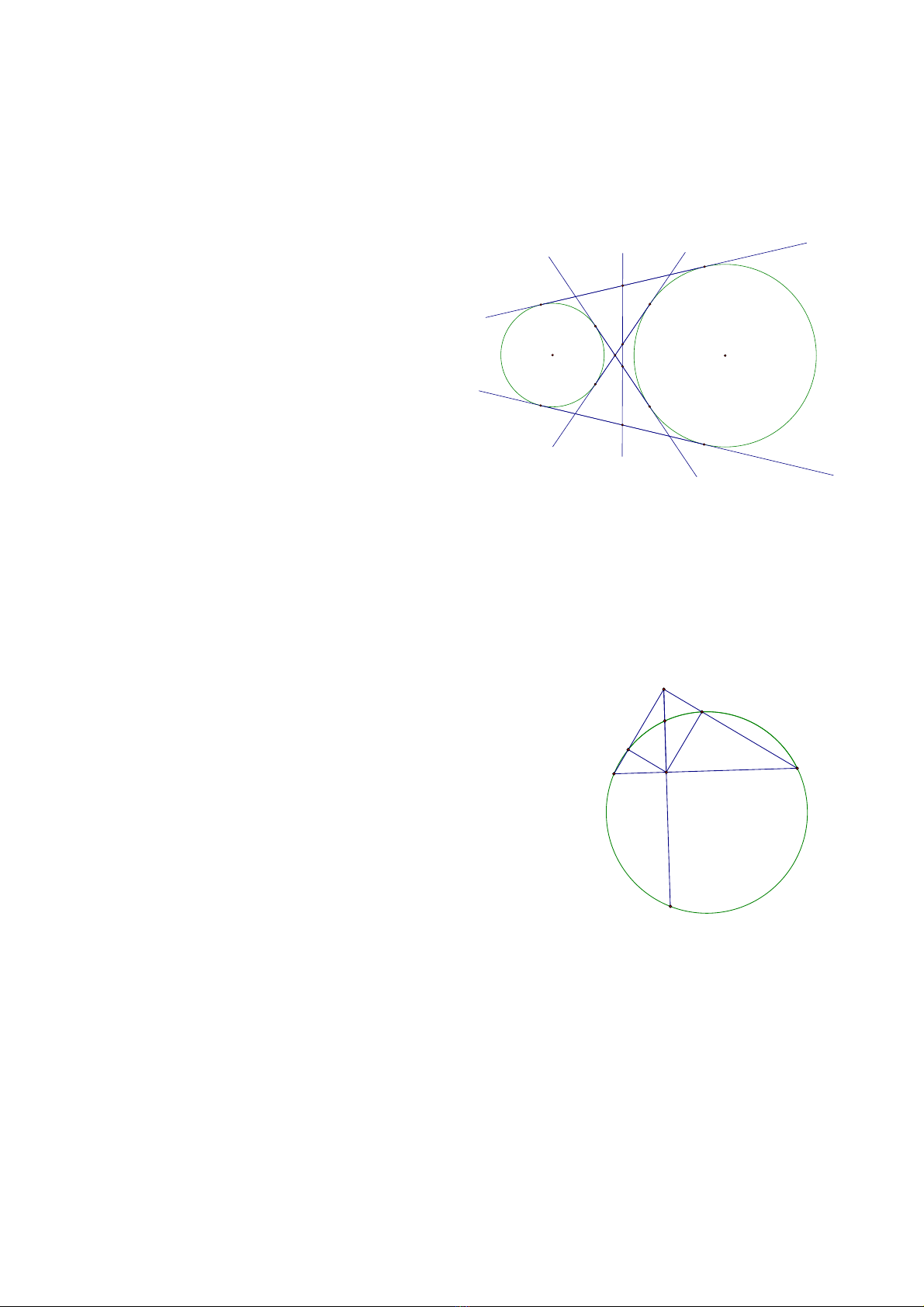
a) Đnh lý 2.1 ịCho hai đng tròn không đng tâm (Oườ ồ 1; R1) và (O2; R2).
T p h p các đi m M có ph ng tích đi v i hai đng tròn b ng nhau là m tậ ợ ể ươ ố ớ ườ ằ ộ
đng th ng, đng th ng này đc g i là tr c đng ph ng c a hai đngườ ẳ ườ ẳ ượ ọ ụ ẳ ươ ủ ườ
tròn (O1) và (O2).
b) Các h quệ ả
Cho hai đng tròn (O) và (I). T đnh lý 2.1 ta suy ra đc các tính ch t sau:ườ ừ ị ượ ấ
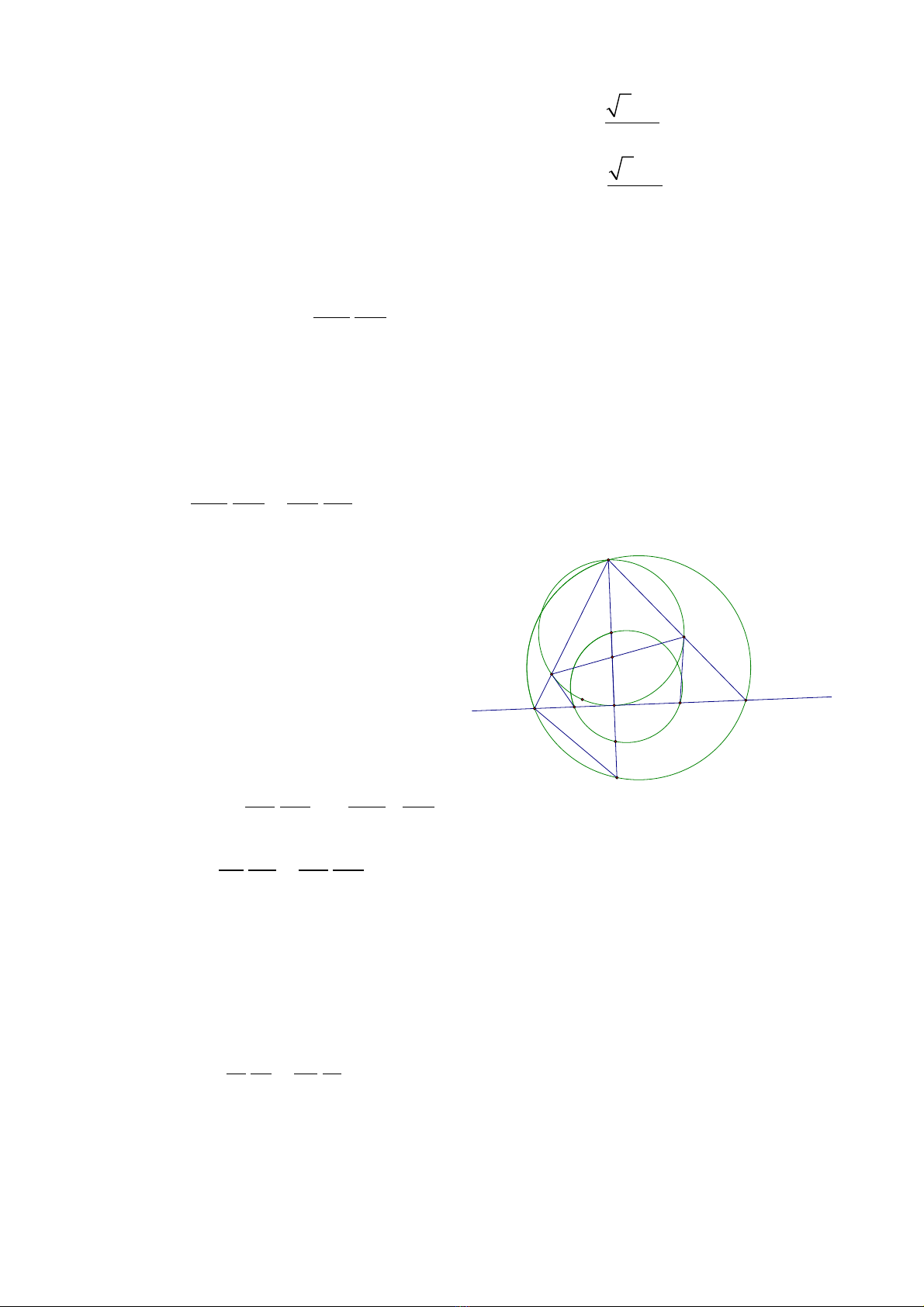
1) Tr c đng ph ng c a hai đng tròn vuông góc v i đng th ngụ ẳ ươ ủ ườ ớ ườ ẳ
n i tâm. ố
2) N u hai đng tròn c t nhau t i A và B thì AB chính là tr c đngế ườ ắ ạ ụ ẳ
ph ng c a chúng.ươ ủ
3) N u đi m M có cùng ph ng tích đi v i (O) và (I) thì đng th ngế ể ươ ố ớ ườ ẳ
qua M vuông góc v i OI là tr c đng ph ng c a hai đng tròn.ớ ụ ẳ ươ ủ ườ
4) N u hai đi m M, N có cùng ph ng tích đi v i hai đng tròn thìế ể ươ ố ớ ườ
đng th ng MN chính là tr c đng ph ng c a hai đng tròn.ườ ẳ ụ ẳ ươ ủ ườ
5) N u 3 đi m có cùng ph ng tích đi v i hai đng tròn thì 3 đi m đóế ể ươ ố ớ ườ ể
th ng hàng.ẳ
6) N u (O) và (I) ti p xúc nhau t i A thì đng th ng qua A và vuôngế ế ạ ườ ẳ
góc v i OI chính là tr c đng ph ng c a hai đng tròn.ớ ụ ẳ ươ ủ ườ
2. Tâm đng ph ngẳ ươ
a) Đnh lý 2.2 ịCho 3 đng tròn (Cườ 1), (C2) và (C3). Khi đó 3 tr c đngụ ẳ
ph ng c a các c p đng tròn trùng nhau ho c song song ho c cùng đi quaươ ủ ặ ườ ặ ặ
m t đi m, đi m đó đc g i là tâm đng ph ng c a ba đng tròn. ộ ể ể ượ ọ ẳ ươ ủ ườ
b)Các h qu . ệ ả
1.N u 3 đng tròn đôi m t c t nhau thì các dây cung chung cùng đi quaế ườ ộ ắ
m t đi mộ ể
2.N u 3 tr c đng ph ng song song ho c trùng nhau thì tâm c a 3ế ụ ẳ ươ ặ ủ
đng tròn th ng hàng.ườ ẳ
3.N u 3 đng tròn cùng đi qua m t đi m và có các tâm th ng hàng thìế ườ ộ ể ẳ
các tr c đng ph ng trùng nhau.ụ ẳ ươ
4.Cách d ng tr c đng ph ng c a hai đng tròn không c t nhauự ụ ẳ ươ ủ ườ ắ
Cho hai đng tròn (Oườ 1) và (O2) không c t nhau, ta có cách d ng tr c đng ắ ự ụ ẳ
ph ng c a hai đng tròn nh sau:ươ ủ ườ ư
1. D ng đng tròn (Oự ườ 3) c t c hai đng tròn (Oắ ả ườ 1) và (O2) l n l t t i ầ ượ ạ
A, B và C, D.
2. Đng th ng AB và CD c t nhau t i Mườ ẳ ắ ạ
4. Đng th ng qua M vuông góc v i Oườ ẳ ớ 1O2 chính là tr c đng ph ng ụ ẳ ươ
c a (Oủ1) và (O2).
III. Các bài t p áp d ngậ ụ
Bài 1. Cho góc
ﾷ
xOy
, A thu c Ox; B,C thu c Oy sao cho ộ ộ
2
.OA OB OC
=
.
Ch ng minh r ng: Đng tròn (ABC) ti p xúc Ox t i A.ứ ằ ườ ế ạ
H ng d nướ ẫ
Gi i s đng tròn (ABC) c t Ox t iả ử ườ ắ ạ
A’.
Ta có OA.OA’ = OB.OC
Theo gi thi t ả ế
2
.OA OB OC
=
nên ta có:
2
. 'OA OA OA
=
y
x
C
B
A
O
OA = OA’
'A A
V y đng tròn (ABC) ti p xúc Ox t i A.ậ ườ ế ạ
Bài 2. Cho ∆ABC có (O, R) và (I, r) l n l t là đng tròn ngo i ti p và ầ ượ ườ ạ ế
đng tròn n i ti p c a ∆ABC. Ch ng minh r ng: ườ ộ ế ủ ứ ằ
2 2
2OI R Rr
= −
H ng d nướ ẫ
G i M là giao c a AI và đng tròn (O). Ta cóọ ủ ườ
2 2
. (1)IA IM R OI
= −
.
∆MIC có
ﾷ
ﾷ
ﾷ
ﾷ
(2)
2
A C
MIC MCI IM MC
+
= = =�
Theo đnh lí Sin trong ∆AMC, MC = 2Rị
sin 2
A
(3).
D ng ự
IH AB
⊥
t i H. Trong ∆IAH cóạ
(4)
sin 2
r
IA A
=
Thay (2), (3), (4) vào (1) ta có:
2 2 2 2
2 2Rr R OI OI R Rr
= − = −�
Bài 3. Cho đng tròn (O,R) và đi m A n m ngoài đng tròn. G i BC ườ ể ằ ườ ọ
là đng kính thay đi c a (O,R). Ch ng minh r ng: Đng tròn (ABC) luôn ườ ổ ủ ứ ằ ườ
đi qua m t đi m c đnh khác Aộ ể ố ị
H ng d nướ ẫ
G i A’ là giao đi m th 2 c a AO và đngọ ể ứ ủ ườ
tròn (ABC).
Ta có
2
. ' .OA OA OB OC R
= =
2
'R
OA OA
=�
.
V y A’ n m trên đng th ng OA c đnhậ ằ ườ ẳ ố ị
và
2
'R
OA OA
=
không đi nên A’ c đnh.ổ ố ị
V y m i đng tròn (ABC) đu đi quaậ ọ ườ ề
đi m A’ c đnhể ố ị
Bài 4. Hai đng tròn ngoài nhau có b n ti p tuy n chung. Ch ng minh r ng: ườ ố ế ế ứ ằ
Trung đi m các đo n ti p tuy n chung n m trên m t đng th ngể ạ ế ế ằ ộ ườ ẳ
M
O
H
I
A
B
C
A'
B
O
A
C
H ng d nướ ẫ
G i I, J, M, N là trung đi m cácọ ể
đo n ti p tuy n chung.ạ ế ế
1 2
2 2
/( ) /( )
,
I O I O
IA IB
= =� �
mà IA = IB
nên
1 2
/( ) /( )I O I O
=� �
. Ch ng minhứ
t ng t ta có J, M, N cùng ph ngươ ự ươ
tích v i (Oớ1) và (O2). V y I, J, M, Nậ
cùng n m trên tr c đng ph ngằ ụ ẳ ươ
c a hai đng tròn. ủ ườ
Bài 5. Cho ∆ABC vuông A, đng cao AH. G i E, F theo th t là ở ườ ọ ứ ự
hình chi u c a H trên AB, AC. Ch ng minh r ng: Khi A, H không thay đi còn ế ủ ứ ằ ổ
B, C thay đi thì:ổ
a) T giác BCFE n i ti pứ ộ ế
b) Đng tròn ngo i ti p t giác BCFE luônườ ạ ế ứ
đi qua 2 đi m c đnhể ố ị
H ng d nướ ẫ
a) Ta có
(góc có c nh t ngạ ươ
ng vuông góc)ứ
Do AEHF là hình ch nh t nênữ ậ
ﾷ
ﾷ
ﾷ
ﾷ
AHF AEF ACH AEF
= =�
mà
ﾷ
ﾷ
0
180AEF BEF
+ =
nên
ﾷ
ﾷ
0
180BEF FCB
+ =
Tứ
giác BECF n i ti pộ ế
b) G i P, Q là giao đi m c a AH v i đng tròn (BEFC)ọ ể ủ ớ ườ
Ta có
2
. .HP HQ HB HC AH= =
.
M t khác ặ
2
. .AP AQ AE AB AH
= =
2
2 2
( )( )
( ) .
AH HP AH HQ AH
AH AH HQ HP HP HQ AH
AH HQ HP
− + =�
+ − − =�
= −�
P
Q
E
F
H
A
B
C
N
M
J
I
C
A
D
B
O1
O2
V y ậ
2
.
HP HQ AH
HP HQ AH
− =
=
gi i h ta đc ả ệ ượ
5 1
2
5 1
2
HP AH
HQ AH
−
=
+
=
P, Q c đnhố ị
V y đng tròn (BEFC) luôn đi qua 2 đi m c đnh P, Q.ậ ườ ể ố ị
Bài 6. Cho đng tròn (O) ti p xúc đng th ng d t i H. Hai đi m M, N di ườ ế ườ ẳ ạ ể
đng trên d sao cho ộ
2
.HM HN k
= −
(
0k
cho tr c ). T M, N k ti p tuy n ướ ừ ẻ ế ế
MA và NB c a (O). ( v i A, B khác H).ủ ớ
a) Ch ng minh r ng: Đng tròn (OMN) luôn đi qua 2 đi m c đnh. ứ ằ ườ ể ố ị
b) Ch ng minh r ng: Đng th ng AB luôn đi qua 1 đi m c đnh. ứ ằ ườ ẳ ể ố ị
H ng d nướ ẫ
a) G i P là giao đi m c a OH v i đng tròn (OMN), cóọ ể ủ ớ ườ
2
. .HM HN HO HP k
= = −
Mà H, O c đnh, k không điố ị ổ
nên P c đnh. V y đng trònố ị ậ ườ
(OMN) luôn đi qua hai đi m cể ố
đnh O, Pị
b) G i IH là đng kính c aọ ườ ủ
(O); E, F là giao đi m c aể ủ
IA, IB v i d.ớ
D th y M, N l n l t làễ ấ ầ ượ
trung đi m c a EH, FHể ủ
Ta có
2
. 2. .2 4HE HF HM HN k
= = −
. D ng đng tròn (IEF) c t IH t i ự ườ ắ ạ
đi m th hai Jể ứ
2
/(IEF)
. . 4
H
HI HJ HE HF k
= = = −�
J c đnh.ố ị
Trong các tam giác vuông∆IHE và ∆IHF. Ta có
2
. .IA IE IB IF IH
= =
T giác ứ
ABEF n i ti pộ ế
ﾷ
ﾷ
IAB EFB
=
(cùng bù
ﾷ
EAB
)
Mà
ﾷ
ﾷ
EFB EJI
=
nên
ﾷ
ﾷ
IAB EJI=
G i K là giao đi m c a AB và IJ ta có t giác AKJE n i ti pọ ể ủ ứ ộ ế
2
/( )
. .
I AKJE
IA IE IK IJ IH
= = =�
K c đnhố ị
V y AB luôn đi qua đi m K c đnhậ ể ố ị
d
P
J
K
F
E
I
N
M
O
H
A
B