
Biên son: Lê Kỳ Hi
Trang 1
A. Chuyên ñ 1: Phương trình mũ
I. Ki"n th#c cơ b&n v hàm s) mũ :
1. Đ+nh nghĩa :
. ...
n
a a a a
=
(tích ca n s a) vi a là cơ s, n là s mũ
Quy ưc :
+
1
a a
=
(vi mi a).
+
0
1
a
=
(vi a khác 0).
Lũy th#a mũ âm :
1
n
n
a
a
−
=
( vi a khác 0;
*
n N
∈
)
Lũy th#a mũ h'u t( : vi
0
a
>
và
, *
m n N
∈
+
( )
m
m
m
nn
n
a a a
= =
.
+
1 1
m
nm
m
n
n
a
a
a
−
= =
.
+
1
n
n
a a
=
.
2. Các tính ch1t :
+ ( )
n n n
ab a b
=
.
+
n
n
n
a a
b b
=
.
+
m n m n
a a a
+
=
.
+
m
m n
n
a
a
a
−
=
.
+
(
)
(
)
.
n m
m n m n
a a a
= =
.
Chuyên ñ : Phương trình – B1t phương
Trình
–
H
5
phương trình mũ
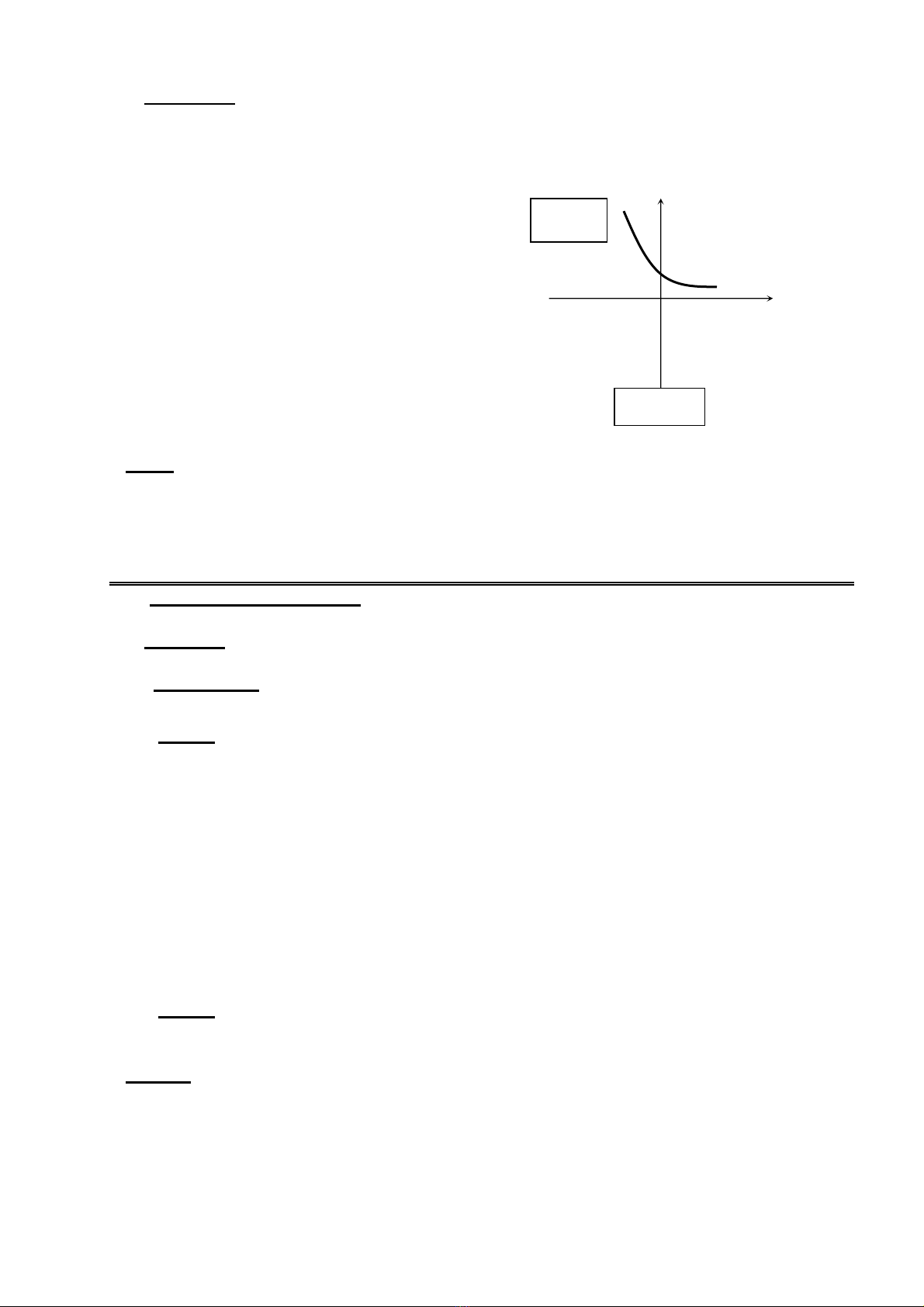
1
a
>
x
y a
=
y
x
1
Biên son: Lê Kỳ Hi
Trang 2
3. Hàm s) mũ :
D-ng :
(
)
0, 1
x
y a a a
= > ≠
.
TXĐ :
D
=
ℝ
.
TGT :
T
+
=
ℝ
.
Tính ñơn ñi3u :
+ 1:
x
a y a
> =
ñ4ng bi6n trên
ℝ
.
+ 0 1:
x
a y a
< < =
ngh8ch bi6n trên
ℝ
.
Đ4 th8 hàm s : hình v: bên
Chú ý :
+ Khi xét lũy th#a vi s mũ 0 và s mũ nguyên âm thì cơ s ph@i khác 0.
+ khi xét lũy th#a vi s mũ không nguyên thì cơ s ph@i dương.
II. Các dng toán thư:ng g;p :
1. Bài toán 1: S= d>ng phương pháp bi"n ñ?i tương ñương
1.1.Phương pháp: Ta s dng phương pháp bi"n ñ#i tương ñương sau.
1.2.
Dng 1: Phương trình dng
(
)
(
)
f x g x
a a=
TH1:
Khi a là mCt hDng s thEa mãn
0 1
a
< ≠
thì
(
)
(
)
( ) ( )
f x g x
a a f x g x
= ⇔ =
.
TH2:
Khi a là mCt hàm ca
x
thì :
( ) ( )
( ) ( )
1
0 1
f x g x
a
a
a a
f x g x
=
< ≠
= ⇔
=
hoHc
( ) ( ) ( )
0
1 0
a
a f x g x
>
− − =
1.3. Dng 2: Phương trình dng
( )
( )
0 1, 0
log
f x
a
a b
a b
f x b
< ≠ >
= ⇔ =
.
Đ;c bi5t :
A
Khi
0
b
=
hoHc
0
b
<
thì k6t luIn ngay phương trình vô nghi3m.
A
Khi
1
b
=
ta vi6t
(
)
( )
0 0
0
f x
b a a a f x
= ⇔ = ⇔ =
0 1
a
< <
x
y a
=
y
x
1
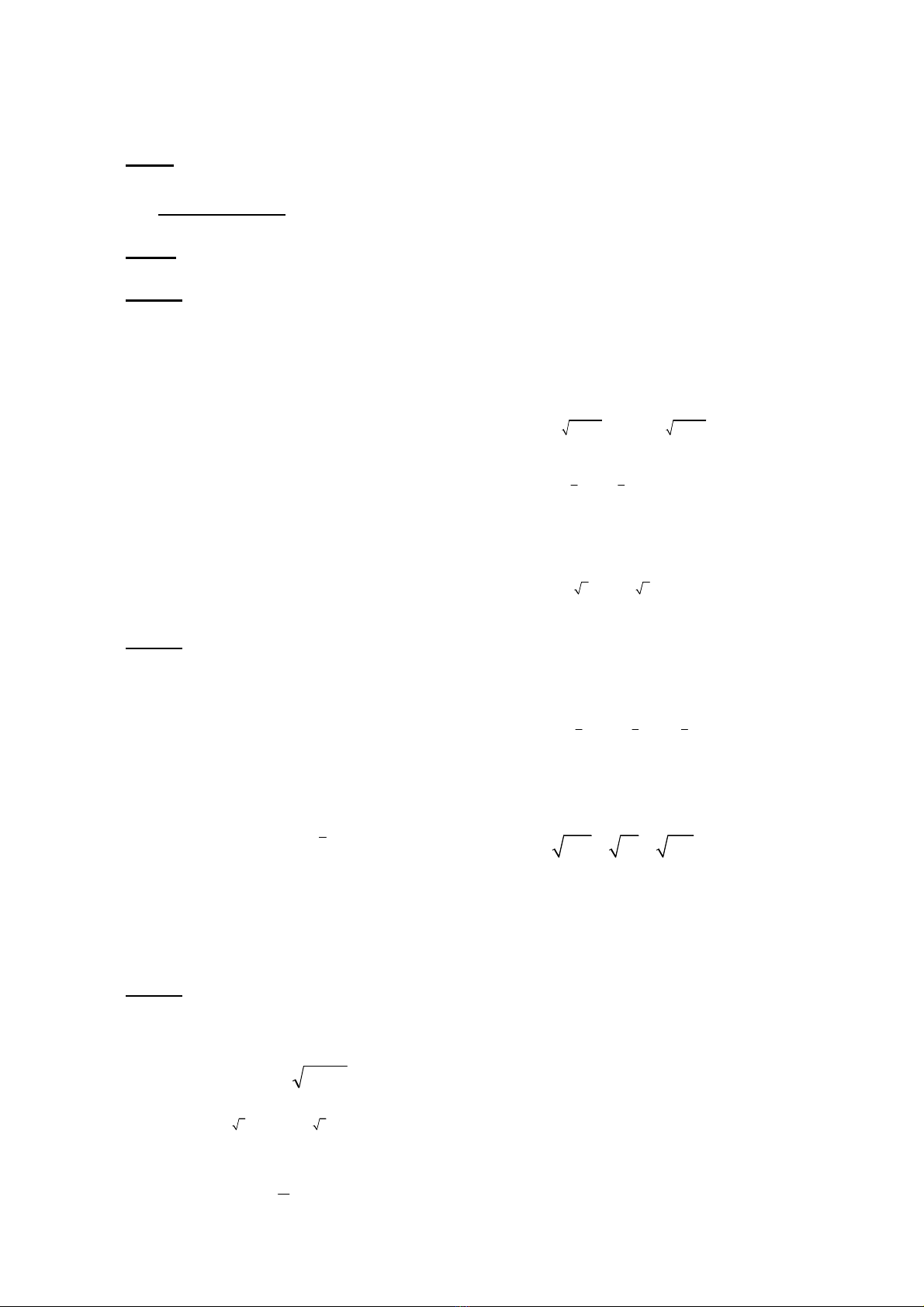
Biên son: Lê Kỳ Hi
Trang 3
A
Khi
1
b
≠
mà b có thL biLu diMn thành
(
)
( )
f x
c c
b a a a f x c
= ⇔ = ⇔ =
.
Chú ý : Trư&c khi bi"n ñ#i tương ñương thì
(
)
f x
và
(
)
g x
ph*i có nghĩa.
1.4. Bài tCp áp d>ng :
Loi 1: Khi cơ s) là mt hEng s).
Dng 1: Cùng mũ, cùng cơ s).
Gi&i các phương trình sau :
1.
3 2cos 1 cos
4 7.4 2 0
x x
+ +
− − =
.
2.
2 2
1 3
16 64 4 3 0
x x− −
− ⋅ + =
.
3.
9 9 3
log log log 27
4 6 2 2 0
x x
− ⋅ + =
.
4.
2 2
2 2 1
9 7 3 2
x x x x x x− − − − −
− ⋅ =
.
5.
2 2
sin cos
9 9 10
x x
+ =
.
6.
1 3
3
64 2 12 0
x x
+
− + =
.
7.
2
cos2 cos
4 4 3
x x
+ =
.
8.
2 2
4 6.2 8 0
x x
− + =
.
9.
2 2
1 2
9 10.3 1 0
x x x x+ − + −
− + =
.
10.
1
2 2 1
x x−
− =
.
Dng 2: Cùng mũ, khác cơ s).
Gi&i các phương trình sau :
1.
2 2 2
15.25 34.15 15.9 0
x x x
− + =
.
2.
1 1 1
6.9 13.6 6.4 0
x x x
− + =
.
3.
3 1
125 50 2
x x x
+
+ =
.
4.
6.9 13.6 6.4 0
x x x
− + =
.
5.
2
4.3 9.2 5.6
x
x x
− =
.
6.
3 3 3
25 9 15 0
x x x
− + =
.
7.
xxx
6242.33.8 +=+ .
8.
20515.33.12
1
=−+
+xxx
.
9.
xxx
543 =+ .
10.
3.8 4.12 18 2.27 0
x x x x
+ − − =
.
Dng 3: Cùng cơ s) , khác mũ.
Gi&i các phương trình sau :
1.
xxx
9133.4
13
−=−
+
.
2.
2 2
2 1 2 2
2 9.2 2 0
x x x x+ + +
− + =
.
3.
1
4 4 3.2
x x x x
+ +
− = .
4.
1 1
5 6.5 3.5 52
x x x
+ −
+ − =
.
5.
( )
1
5 7
2
1,5 3
x
x
+
−
=
. 6.
( ) ( )
7 1 2
0,5 . 0,5 2
x x+ −
=
.

Biên son: Lê Kỳ Hi
Trang 4
7.
2
2 3
1
1
7
7
x x
x
− −
+
=
.
8.
(
)
2 3
2 1 2 1
x−
− = +
.
9.
(
)
3
5 9.5 27.125 5 64
x x x x− −
+ + + =
.
10.
( )
1
2
2
4
2
22
11
+
=
+
+−+ xxxx
.
Dng 4: Tích cơ s) bEng 1.
Gi&i các phương trình sau :
1.
(
)
(
)
2 3 2 3 14
x x
− + + =
.
2.
(
)
(
)
4 15 4 15 8
x x
− + + =
.
3.
(
)
(
)
cos cos
5
7 4 3 7 4 3
2
x x
+ + − =
.
4.
(
)
(
)
7 3 5 7 3 5 14.2
x x
x
+ + − = .
5.
(
)
(
)
2 3 2 3 2
x x
x
+ + − =
.
6.
(
)
(
)
2 1 2 1 2 2 0
x x
− + + − =
.
7.
(
)
(
)
sin sin
5 2 6 5 2 6 2
x x
+ + − =
.
8.
(
)
(
)
3
3 5 16 3 5 2
x x
x
+
+ + − = .
9.
(
)
(
)
(
)
(
)
32.432.34732 +=−+++
xx
.
10.
(
)
( )
(
)
32
4
3232
121
2
2
−
=−++
−−− xxx
.
Loi 2: Khi cơ s) là mt hàm cPa x.
Gi&i các phương trình sau :
1.
( ) ( )
sin 2 3cos
2 2
2 2
x x
x x x x
−
+ − = + − .
2.
( )
( )
2
2
4
3 5 2 2
3 6 9
x x
x x
x x x
+ −
− +
− = − + .
3.
(
)
2
2
1
x
x x
−
− =
.
4.
( )
2
1
2
1 1
x
x x
−
− + =
.
5.
( )
2
4
2
2 2 1
x
x x
−
− + =
.
6.
(
)
2
2
1
x
x x
−
− =
.
7.
2
2
1
x x
x
−
=
.
8.
( )
2
2
2
3 3
x x
x x
−
− = − .
9.
( ) ( )
3
1 1
3
1 1
x x
x x
− −
− = − .

Biên son: Lê Kỳ Hi
Trang 5
2. Bài toán 2: S= d>ng phương pháp logarit hóa và ñưa v cùng cơ s).
2.1. Phương pháp: Đ/ chuy/n 0n s kh1i s mũ lũy th2a ta có th/ logarit theo cùng m6t cơ s
c* 2 v" c7a phương trình, ta có các d8ng :
2.2.
Dng 1: Phương trình dng :
( )
( )
0 1, 0
log
f x
a
a b
a b
f x b
< ≠ >
= ⇔ =
.
2.3.
Dng 2: Phương trình dng cơ s) khác nhau và s) mũ khác nhau.
(
)
(
)
(
)
(
)
( ) ( )
log log .log
f x g x f x g x
a a a
a b a b f x g x b
= ⇔ = ⇔ =
.
HoHc
(
)
(
)
( ) ( )
log log .log
f x g x
b b b
a b f x a g x
= ⇔ = .
Đ;c bi5t
: Cơ s) khác nhau nhưng s) mũ bEng nhau
Khi
( ) ( )
( ) ( )
(
)
( )
0
1 0
f x
f x f x
a a
f x g x a b f x
b b
= ⇔ = ⇔ = = ⇔ =
.
Chú ý :
9 Phương pháp áp dng khi có d8ng tích – thương c7a các hàm s mũ.
9 M6t s phương trình c=n rút g?n trư&c khi logarit hóa.
2.4. Bài tCp áp d>ng :
Gi&i các phương trình sau :
1.
1
5 .8 500
x
xx
−
=.
2.
2
2 3
2
3 .4 18
x
xx
−
−
=
.
3.
2
4 2
2 .5 1
x x− −
=
.
4.
2
2
3
2
2
x x−
=
.
5.
4
2
8 4.3
x
x
x
−
+
=.
6.
1 1
2 1
2 2
4 3 3 2
x x
x x
− +
−
−=−.
7.
(
)
2
0,5
log sin 5sin .cos 2
1
4
9
x x x+ +
=
.
8.
1 2 3 1
5 5 5 3 3 3
x x x x x x
+ + + +
+ + = + + .
9.
2 2
3 2 6 2 5
2 3 3 2
x x x x x x
+ + − + −
− = −
.
10.
(
)
2
log 4
32
x
x
+
=
.
11.
2
3 .2 1
x x
=
.
12.
1
4
3 .9
27
x x
x
−
=.


























