
II. ĐỘNG HỌC
Chương 3 : ĐỘNG HỌCĐIỂM
-Điểm là mô hình đơn giản nhất củađốitượng khảo sát
-Đường mà điểm vạch ra trong không gian trong quá trình chuyển
động gọi là quỹ đạo.
-Phương trình mô tảchuyểnđộng củađiẻm gọi là phương trình
chuyểnđộng củađiểm
- Ba phương pháp: véc tơ, toạ độ đề các, toạ độ tựnhiên được sử
dụng để mô tảchuyểnđộng củađiểm
1. Phương pháp véc tơ
1.2. Phương trình chuyểnđộng củađiểm
)(trr
O
M
r
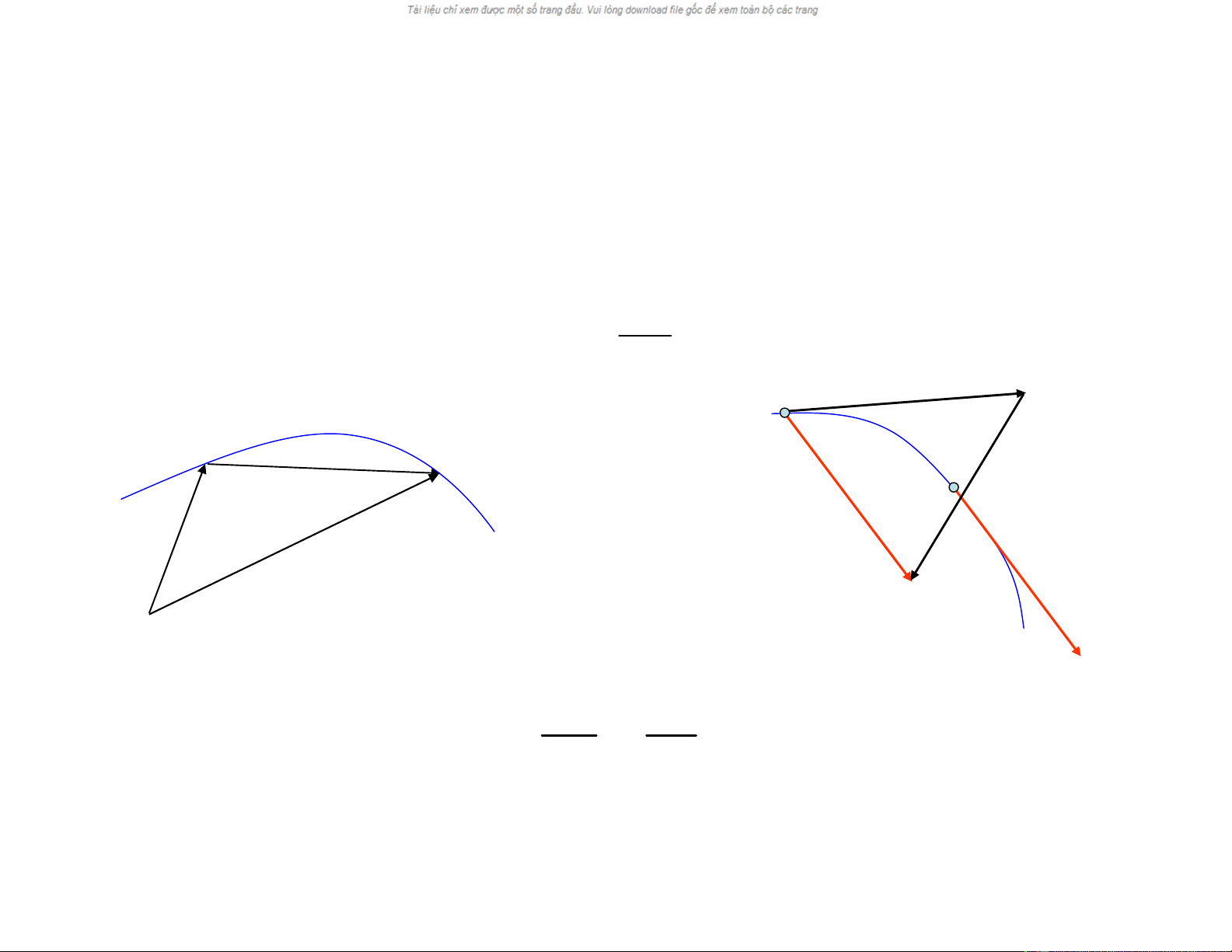
1.2. Vận tốc chuyểnđộng củađiểm
Quãng đường mà điểm M dịch chuyển trong khoảng thời gian t là
cung MM1, khi t đủ nhỏr được coi là dịch chuyển củađiểm M.
- Vận tốc trung bình củađiểm M dịch chuyển trong khoảng thời
gian t được tính như sau:
t
r
vtb
M(t) M1(t+t)
O
r
r
1
r
M(t)
M1(t+t)
1
v
v
v
1
v
- Vận tốc của M tại thờiđiểm t được tính theo công thức sau:
r
dt
rd
t
r
tv
t
lim
0
)(
- Vận tốc củađiểm bằng đạo hàm bậc nhất theo thời gian của bán
kính véc tơ định vị điểm. Thứnguyên [ Chiều dài/thời gian], m/s

1.3. Gia tốc chuyểnđộng củađiểm
- Gia tốc chuyểnđộng củađiểm M tại thờiđiểm t là đạilượng véc tơ
thểhiện sựbiến thiên vận tốc theo thời gian.
rv
dt
vd
t
v
tw
t
lim
0
)(
Véc tơ gia tốc luôn hướng vềphía lõm của quỹ đạo. Thứnguyên
[chiều dài/ thời gian2], m/s2
1.4. Phán đoán tính chất chuyểnđộng củađiểm
Chuyểnđộng nhanh dần hoặc chậm dần củađiểmđược xem xét
thông qua tích vô hướng của và
2. Phương pháp toạđộtựnhiên
Khi biết quỹ đạo củađiểmngười ta khảo sát chuyểnđộng củađiểm
bằng phương pháp tọađộ tựnhiên.
2.2. Phương trình chuyểnđộng củađiểm
Chọn một gốc tọađộ O và một chiềudương của quỹ đạo.
v
w
OM
S
s = s(t)
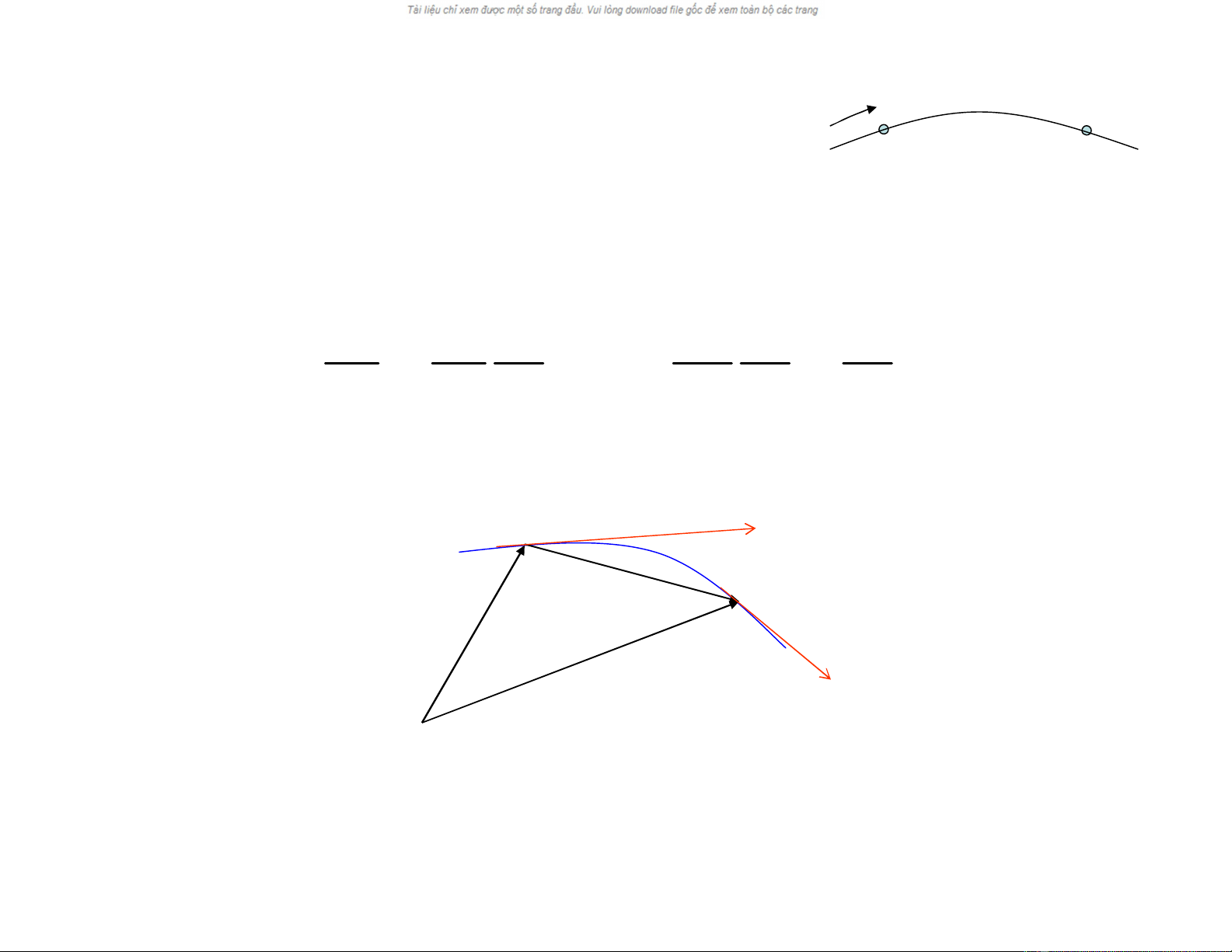
2.2. Vận tốc chuyểnđộng củađiểm
- Từ định nghĩa vềvận tốc
.lim)( 0v
dt
ds
dt
ds
s
r
dt
ds
ds
rd
dt
rd
tv t
-Ở đây véc tơ đơn vịtrên tiếp tuyến tại M
r
r
r
r
1
M
M1
2.3. Gia tốc chuyểnđộng củađiểm
Từ định nghĩa gia tốc:
O

ds
d
dt
ds
dt
sd
dt
d
dt
ds
dt
sd
dt
ds
dt
d
dt
vd
tw
...)(
2
2
22
- Trong đó: vuông góc với véc tơ tại M, gọi là
phương pháp tuyến chính tại M có véc tơ đơn vịlà
k là độ cong và là bán kính cong của quỹ đạo tại M
- Mặt phẳng tạo bởiphương tiếp tuyến và pháp tuyến chính tại M
gọi là mặt phẳng mật tiếp của quỹ đạo tại M.
- Hệtoạđộnhận M làm gốc ( , , ) gọi là hệtọađộ tựnhiên.
- Công thức tổng quát:
s
ds
d
s
0
lim
n
1
lim
0
k
ds
d
sds
d
t
n
b
n
v
dt
sd
dt
vd
tw
..)( 2
2
2




















![Bộ câu hỏi lý thuyết Vật lý đại cương 2 [chuẩn nhất/mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251003/kimphuong1001/135x160/74511759476041.jpg)
![Bài giảng Vật lý đại cương Chương 4 Học viện Kỹ thuật mật mã [Chuẩn SEO]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250925/kimphuong1001/135x160/46461758790667.jpg)




