
1
Chương 9. Chuẩn độ kết tủa
Lâm Ngọc Thụ
Cơ sở hóa học phân tích. NXB Đại học quốc gia Hà Nội 2005.
Từ khoá: Cơ sở hóa học phân tích, Chuẩn độ kết tủa, Chuẩn độ, Đường chuẩn độ hỗn
hợp, Chất chỉ thị hóa học.
Tài liệu trong Thư viện điện tử ĐH Khoa học Tự nhiên có thể được sử dụng cho mục
đích học tập và nghiên cứu cá nhân. Nghiêm cấm mọi hình thức sao chép, in ấn phục
vụ các mục đích khác nếu không được sự chấp thuận của nhà xuất bản và tác giả.
Mục lục
Chương 9 Chuẩn độ kết tủa........................................................................................... 2
9.1 Đường chuẩn độ kết tủa......................................................................................... 2
9.2 Ý nghĩa của chữ số khi tính đường chuẩn độ........................................................ 4
9.3 Những yếu tố ảnh hưởng đến tính rõ ràng của điểm cuối..................................... 4
9.4 Đường chuẩn độ hỗn hợp....................................................................................... 7
9.5 Những chất chỉ thị hóa học của phương pháp chuẩn độ kết tủa......................... 10

2
Chương 9
Chuẩn độ kết tủa
Những phương pháp chuẩn độ dựa trên sự tạo thành muối bạc ít tan là những phương
pháp phân tích đã được biết từ lâu. Cho đến bây giờ, những phương pháp đó vẫn thường được
sử dụng để xác định bạc và những ion như clorua, bromua, iođua và tioxianat. Ứng dụng
những phương pháp chuẩn độ kết tủa trong đó chất chuẩn không phải là muối bạc mà là
những hợp chất khác còn tương đối hạn chế.
9.1 Đường chuẩn độ kết tủa
Trước khi nghiên cứu chương này, sinh viên cần ôn lại những luận điểm cơ sở về độ tan
của kết tủa ở chương 5.
Đường chuẩn độ có ích cho việc lựa chọn chỉ thị và cả phép tính sai số trong chuẩn độ. Ví
dụ sau đây sẽ chỉ rõ cách xây dựng đường chuẩn độ kết tủa xuất phát từ tích số tan của kết tủa
tạo thành.
Ví dụ: Hãy dựng đường chuẩn độ 50 ml dung dịch KBr 0,005 M bằng dung dịch AgNO3
0,010 M.
Chúng ta tính pBr và pAg mặc dù thường chỉ cần tính một trong 2 đại lượng ấy là đủ (lựa
chọn đại lượng nào là do ảnh hưởng của các ion đến tính chất của chỉ thị quyết định).
Điểm đầu: Ở đầu phép chuẩn độ chúng ta có dung dịch Br– 0,00500 M, Ag+ chưa có. Do
đó pBr– = –log(5,00.10–3) = 2,30; giá trị pAg không xác định được.
Điểm sau khi thêm 5 ml thuốc thử: Nồng độ ion bromua trong trường hợp này hạ thấp do
kết tủa được tạo thành và do cả sự pha loãng dung dịch. Do đó:
3
NaBr
50,00 0,005 5,00 0,010
C3
50,00 5,00
−
,64.10M
×
−×
==
+
Thành phần đầu ở tử số là lượng milimol NaBr ban đầu, thành phần thứ 2 là lượng
milimol AgNO3 thêm vào. Ion bromua tồn tại trong dung dịch do phần NaBr chưa bị chuẩn và
do độ tan của AgBr, do đó nồng độ chung của Br– lớn hơn nồng độ NaBr chưa bị chuẩn một
lượng bằng độ tan của kết tủa, nghĩa là:
[Br–] = 3,64.10–3 + [Ag+]

3
Số hạng thứ 2 trong tổng số đó phản ánh sự đóng góp của AgBr vào nồng độ Br–, mà mỗi
ion Br– được tạo thành từ một ion Ag+. Nếu nồng độ NaBr không quá nhỏ thì có thể bỏ qua số
hạng thứ 2, nghĩa là nếu:
[Ag+] << 3,64.10–3 ion.g/l
thì
[Br–] ≈ 3,64.10–3 ion.g/l
pBr– = –log(3,64.10–3) = 2,439 = 2,44
Có thể tính đại lượng pAg một cách thuận tiện khi sử dụng logarit âm để diễn tả tích số
tan của AgBr:
–log([Ag+][Br–]) = –logT = –log(5,2.10–13);
–log[Ag+] – log[Br–] = –logT = 12,28
hoặc
pAg + pBr = pT =12,28
pAg = 12,28 – 2,44 = 9,84
Có thể tính một cách tương tự nồng độ Br– và Ag+ ở các điểm khác của đường chuẩn độ
cho đến điểm tương đương.
Điểm tương đương: Ở điểm này không có dư cả AgNO3 và NaBr, do đó:
[Ag+] = [Br–]
Thực hiện những phép thay thế tương ứng trong phương trình tích số tan chúng ta có:
[Ag+] = [Br–] = 13
5,2.10− = 7,21.10–7 mol/l
pAg = pBr = –log(7,21.10–7) = 6,14
Điểm sau khi thêm 25,10 ml thuốc thử: Trong dung dịch có dư AgNO3, do đó:
3
5
AgNO
25,10 0,010 50,00 0,005
C 1,33.10 M
75,10
−
×
−×
==
và
[Ag+] = 1,33.10–5 + [Br–] ≈ 1,33.10–5 ion.g/l

4
Thành phần thứ 2 bên phải phản ánh lượng ion Ag+ đi vào dung dịch do độ tan
của AgBr, thường có thể bỏ qua đại lượng đó:
pAg = –log(1,33.10–5) = 4,876 = 4,88
pBr–= 12,28 – 4,88 = 7,40
Những điểm bổ sung để xây dựng đường chuẩn độ sau điểm tương đương có thể thu được
bằng cách tương tự.
9.2 Ý nghĩa của chữ số khi tính đường chuẩn độ
Tính đường chuẩn độ ở gần điểm tương đương thường không có độ chính xác cao bởi vì
nó dựa trên cơ sở sử dụng hiệu số hai số lớn gần nhau về giá trị. Ví dụ, khi tính nồng độ
AgNO3 sau khi thêm 25,10 ml dung dịch AgNO3 0,010 M; tử số trong công thức tính (0,2510
– 0,2500) chỉ chứa 2 chữ số có nghĩa. Do đó, nồng độ AgNO3 trong trường hợp tốt nhất cũng
chỉ có thể tính với độ chính xác đến 2 chữ số có nghĩa. Hơn nữa để làm giảm sai số khi làm
tròn, chúng ta kiểm tra phép tính đó với độ chính xác đến 3 số lẻ và làm tròn sau khi tính pAg.
Khi làm tròn hàm số p, cần nhớ rằng (chương 2) logarit gồm có phần đặc tính (những chữ
số ở bên trái dấu phẩy ngăn cách với số lẻ thập phân) và phần định trị; phần đặc tính được
diễn tả chỉ bằng số số nguyên trong giá trị lấy logarit. Do đó chỉ có thể làm tròn phần định trị
đến số tương ứng của chữ số có nghĩa.
Trong ví dụ đã được phân tích trên đây, các điểm của đường chuẩn độ đủ tách biệt khỏi
bước nhảy chuẩn độ. Chúng ta có khả năng tính bước nhảy với độ chính xác cao. Chúng ta có
thể đưa ra pAg ở điểm đầu bằng 2,301, nhưng độ chính xác đó ít có ý nghĩa bởi vì, trước hết
chúng ta quan tâm đến vùng gần điểm tương đương. Do đó, ở đây cũng như khi xây dựng các
đường chuẩn độ khác, chúng ta sẽ làm tròn hàm số p đến 2 số sau dấu phẩy. Độ chính xác
không cao cũng hoàn toàn thỏa mãn bởi vì điều quan trọng cần biết là sự biến đổi của hàm số p
chứ không phải là giá trị tuyệt đối của nó. Những biến đổi đó đủ lớn và ít phụ thuộc vào sai số
trong phép tính.
9.3 Những yếu tố ảnh hưởng đến tính rõ ràng của điểm cuối
Để có sự rõ ràng và do đó dễ dàng xác định được điểm cuối của phép chuẩn, điều cần
thiết nhất cần biết là ở gần điểm tương đương chỉ cần thêm một lượng nhỏ chất chuẩn cũng
làm cho hàm số p biến đổi rõ rệt. Do đó, cần thiết phải xét những yếu tố ảnh hưởng đến giá trị
bước nhảy của hàm số p trong quá trình chuẩn độ.
Nồng độ thuốc thử: bảng 9.1 dẫn ra những kết quả tính theo phương pháp đã được phân
tích trong ví dụ dẫn ra trên đây. Tính toán được tiến hành đối với 3 nồng độ ion bromua và
ion bạc khác nhau 10 lần. Những kết quả tính toán pAg đối với cả 3 trường hợp được diễn tả
trên hình 9.1, minh họa rõ ràng ảnh hưởng của nồng độ đến đường chuẩn độ. Khi tăng nồng
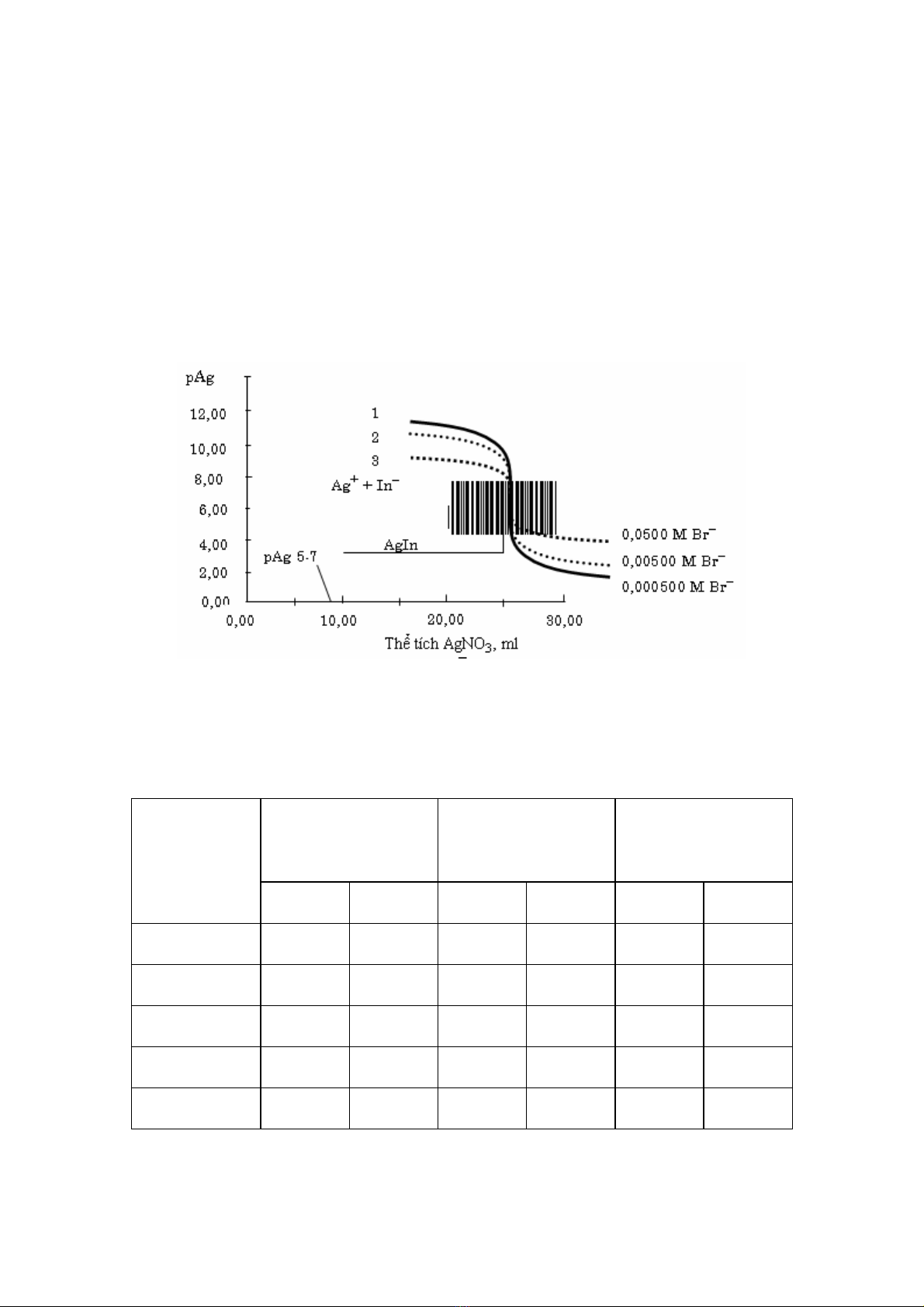
5
độ chất cần chuẩn và chất chuẩn, sự biến đổi pAg ở vùng gần điểm tương đương trở nên rõ
hơn.
1. Chuẩn độ dung dịch Br– 0,0500 M bằng dung dịch Ag+ 0,100 M.
2. Chuẩn độ dung dịch Br– 0,00500 M bằng dung dịch Ag+ 0,0100 M.
3. Chuẩn độ dung dịch Br– 0,000500 M bằng dung dịch Ag+ 0,00100 M.
Hiện tượng tương tự cũng được quan sát thấy nếu thay thế pAg trên trục tung bằng pBr.
Hình 9.1
Ảnh hưởng của nồng độ thuốc thử đến đường chuẩn độ 25,0 ml dung dịch NaBr
Bảng 9.1 Sự biến đổi pAg và pBr trong quá trình chuẩn độ những dung dịch có nồng
độ khác nhau
Chuẩn 25,0 ml Br–
0,0500 M bằng
AgNO3 0,100 M
Chuẩn 25,0 ml Br–
0,00500 M bằng
AgNO3 0,010 M
Chuẩn 25,0 ml Br–
0,00500 M bằng
AgNO3 0,001 M
Thể tích
AgNO3 (ml)
pAg pBr pAg pBr pAg pBr
0,00 – 1,30 – 2,30 – 3,30
10,00 10,68 1,60 9,68 2,60 8,68 3,60
20,00 10,13 2,15 9,13 3,15 8,13 4,15
23,00 9,72 2,56, 8,72 3,56 7,72 4,56
24,90 8,41 3,87 7,41 4,87 6,50 5,78a
























![Bài tập so sánh hơn và so sánh nhất của tính từ [kèm đáp án/mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250808/nhatlinhluong27@gmail.com/135x160/77671754900604.jpg)
![Tài liệu tham khảo Tiếng Anh lớp 8 [mới nhất/hay nhất/chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250806/anhvan.knndl.htc@gmail.com/135x160/54311754535084.jpg)




![Tài liệu Lý thuyết và Bài tập Tiếng Anh lớp 6 [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250802/hoihoangdang@gmail.com/135x160/18041754292798.jpg)





