V t lý l p 12 ậ ớ
CÔNG TH C TÍNH NHANH KHI LÀM BÀI T P TR C NGHI MỨ Ậ Ắ Ệ
I.CON L C LÒ XOẮ:
m
k
=
ω
,
k
m
T
π
2=
,
m
k
f
π
2
1
=
1.Công th c đ c l p:ứ ộ ậ
2
2
2
2A
v
x=+
ω
T đó tìm v, A ho c x t i các th i đi mừ ặ ạ ờ ể
Li đ xộ- A 0 + A
V n t c vậ ố 0
A
ω
±
0
Gia t c aố
A
2
ω
+
0
A
2
ω
+
L c h i ph cự ồ ụ kA 0 kA
2. Đ nh lu t b o toàn c năng:ị ậ ả ơ
22
max0
22
2
1
2
1
2
1
2
1kAmvkxmv ==+
3.Tìm pha ban đ u ng v i th i đi m t= 0:ầ ứ ớ ờ ể
* T i v trí cân b ng: x=0 , v>0 ạ ị ằ
⇒
v<0
⇒
2
π
ϕ
=
*T i v trí biên ạ ị
πϕ
ϕ
=⇒−=
=⇒=
Ax
Ax 0
* T i v trí b t kỳ có li đ ạ ị ấ ộ
0
0
00 ,x
v
Tanvvxx
ω
ϕ
±
±
=⇒±=±=
4..L c tác d ng lên giá đ , dây treoự ụ ỡ :
- Con l c lò xo n m ngang: ắ ằ
KxlKF =∆=
- Con l c lò xo th ng đ ng: ắ ẳ ứ
)( 0xlKF ±∆=
; l c đàn h i:ự ồ
C c đ i khi x=+Aự ạ
C c ti u : +n u ự ể ế
0
lA ∆<
thì x= -A
⇒
)(
0
AlKF −∆=
,
+ n u ế
0
lA ∆>
thì
0
lx ∆=
(lò xo ko bi n d ng ) ế ạ
⇒
F=0
S u T mư ầ 1
V t lý l p 12 ậ ớ
III.SÓNG C - GIAO THOA – SÓNG D NG:Ơ Ừ
ω
π
λ
2
v
f
v
vT ===
đ l ch pha: ộ ệ
λ
π
ϕ
d2
=∆
*V trí c c đ i : ị ự ạ
),.........3,2,1.(
12 ±±±==− kkdd
λ
, khi đó A= 2a
*V trí c c ti u : ị ự ể
),.........3,2,1.()
2
1
(
12 ±±±=+=− kkdd
λ
, khi đó A= 0
1.Xác đ nh tr ng thái dao đ ng c a 1 đi m M trong mi n giao thoa gi a 2 sóng:ị ạ ộ ủ ể ề ữ
Xét:
k
dd =
−
λ
12
nguyên thì M dao đ ng v i Aộ ớ ma x, n u k l M ko dao đ ng A=0ế ẻ ộ
2.Bi u th c sóng t ng h p t i M trong mi n giao thoa:ể ứ ổ ợ ạ ề
)cos( Φ+= tAu M
ω
v i: ớ
λ
π
)(
cos2 12 dd
aAM
−
=
và
λ
π
)( 21 dd +
−=Φ
3.Tìm s đi m dao đ ng c c đ i, c c ti u trong mi n giao thoa:ố ể ộ ự ạ ự ể ề
*C c đ i: ự ạ
λλ
2121 SS
k
SS ≤≤−
( k c Sể ả 1, S2)
* C c ti u: ự ể
2
1
2
12121 −<<−−
λλ
SS
k
SS
Chú ý l y k nguyênấ
4. V trí đi m b ng, nút:ị ể ụ
B ng: ụ
22
21
1
λ
k
SS
d+=
Nút:
2
)
2
1
(
2
21
1
λ
++= k
SS
d
Đi u ki n: 0ề ệ
211 SSd ≤≤
5.Đi u ki n đ có sóng d ng:ề ệ ể ừ
a.Hai đ u c đ nhầ ố ị ;
Chi u dài: ề
2
λ
kl =
s múi sóng k=ố
λ
l2
, s b ng k, s nút (k+1)ố ụ ố
T n s : ầ ố
l
v
kf
f
v
kl
f
v
22 =→=→=
λ
a.M t đ u c đ nhộ ầ ố ị ; Chi u dài: ề
2
)
2
1
(
λ
+= kl
, s b ng ( k+1), s nút (k+1)ố ụ ố
S u T mư ầ 2
V t lý l p 12 ậ ớ
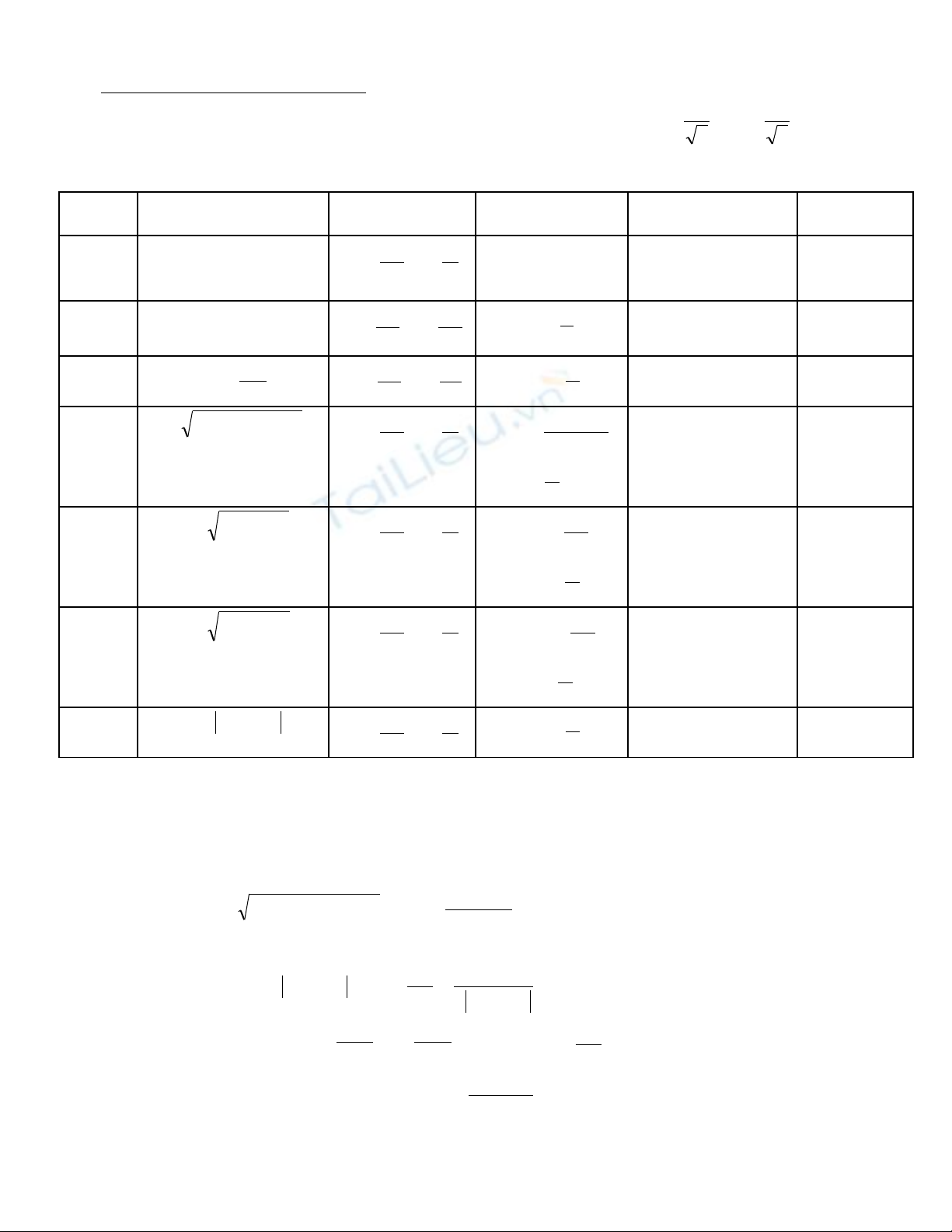
IV.DÒNG ĐI N XOAY CHI U:Ệ Ề
1.N uế
)cos()cos( 00
ϕωω
+=⇒= tUutIi
và ng c l i; ta luôn có ượ ạ
2
0
I
I=
;
2
0
U
U=
2.Đ nh lu t Ohm cho các lo i đo n m ch:ị ậ ạ ạ ạ
Đo nạ
m chạĐi n trệ ở ĐL Ohm Đ l ch pha ộ ệ
iu /
ϕ
Gi n đ véc tả ồ ơ Công su tấ
Ch cóỉ
R
R
R
U
I
R
U
I== ,
0
0
0=
ϕ
P=UI=RI2
Ch cóỉ
L
ω
LZ L=
LL Z
U
I
Z
U
I== ,
0
0
2
π
ϕ
=
P=0
Ch cóỉ
C
C
ZL
ω
1
=
Zc
U
I
Zc
U
I== ,
0
0
P=0
RLC
22 )( CL ZZRZ −+=
Z
U
I
Z
U
I== ,
0
0
Z
R
R
ZZ CL
=
−
=
ϕ
ϕ
cos
,tan
P=UIcosϕ
=RI2
RL
22
L
ZRZ +=
Z
U
I
Z
U
I== ,
0
0
Z
R
R
Z
L
=
=
ϕ
ϕ
cos
,tan
P=UIcosϕ=
RI2
RC
22
C
ZRZ +=
Z
U
I
Z
U
I== ,
0
0
Z
R
R
ZC
=
−=
ϕ
ϕ
cos
,tan
P=UIcosϕ=
RI2
LC
CL
ZZZ −=
Z
U
I
Z
U
I== ,
0
0
P=0
3.Xác đ nh đ l ch pha gi a 2 hdt t c th i uị ộ ệ ữ ứ ờ 1, u2:
iuiuuu /2/12/1
ϕϕϕ
−=
* Hai đo n m ch vuông pha : ạ ạ
1tantan 21 −=
ϕϕ
4.M ch RLC tìm đk đ I max ; u,i cùng pha ; ho c cosạ ể ặ
ϕ
=max:
CL ZZ =
hay
1
2=
ω
LC
N u m c thêm t C thì t trên tìm Cế ắ ụ ừ td n u Cếtd> C ghép song song, ng c l iượ ạ
5.Tìm Um :
R
CL
CLR U
UU
UUUU −
=−+=
ϕ
tan,)( 22
6.Tìm đi u ki n đ P=max:ề ệ ể
* Khi R thay đ i: ổ
CL
CL
ZZ
U
R
U
PZZR −
==−= 22
,
22
max
* Khi L ho c C thay đ i: ặ ổ
22
1
,
1
ωω
C
L
L
C==
lúc đó
R
U
P
2
max =
7.Tìm đk đ Uểc đ t max khi C thay đ i: ạ ổ
C
Z
ZR
Z
L
L
C⇒
+
=22
* N u tìm UếL khi L thay đ i thì thay C b ng Lổ ằ
S u T mư ầ 3
V t lý l p 12 ậ ớ
V.MÁY BI N TH - M C T I:Ế Ế Ắ Ả
1.M c sao:ắ Ud=
p
U3
n u t i đ i x ng Iế ả ố ứ t i ả=
tai
p
Z
U
Công su t tiêu th m i t i ấ ụ ỗ ả
2
cos ttttp IRIUP ==
ϕ
2.Máy bi n th :ế ế R=0 ta luôn có;
2
1
1
2
1
2
I
I
N
N
U
U==
VI. M CH DAO Đ NG LC:Ạ Ộ
Các đ i l ng đ c tr ngạ ượ ặ ư q, i=q’ , L , C
Ph ng trình vi phânươ
0"0
1
"2=+⇔=+ qqq
LC
q
ω
T n s góc riêngầ ố
LC
1
=
ω
Nghi m c a pt vi phânệ ủ
)cos(
0
ϕω
+= tQq
Chu kỳ riêng
LCT
π
2=
Năng l ng dao đ ngượ ộ
td WW ,
dao đ ng v i t n s f’=2f, chu kỳ T’=ộ ớ ầ ố
2
T
quCuq
C
Wd2
1
2
1
2
122 ===
2
2
1LiWd=
2
0
2
0
22
2
1
2
1
2
1
2
1LIQ
C
Liq
C
W==+=
1.Bi u th c c ng đ dòng đi nể ứ ườ ộ ệ :
⇔+= )cos(
0
ϕωω
tQi
)cos(
0
ϕω
+= tIi
v i *ớ
L
C
U
LC
Q
QI 0
0
00 ===
ω
*
00 CUQ =
;
0
0
22 I
Q
LCT
ππ
==
2.Máy thu, có m c m ch LC , Tìm C:ắ ạ - N u bi t f : ế ế
Lf
C22
4
1
π
=
,
- n u bi t ế ế λ:
cL
C2
2
4
π
λ
=
v i c=3.10ớ8m/s
* Khi m c Cắ1 t n s fầ ố 1, khi m c Cắ2 t n s fầ ố 2 ; t n s f khi : - ầ ố
2
2
2
1
2
21 :fffntCC +=
-
2
2
2
1
2
21
111
:fff
ssCC +=
3.Tìm d i b c sóng ả ướ
λ
ho c f ặ:
LCc
πλ
2=
t đó: ừ
maxmin
λλλ
≤≤
LC
f
π
2
1
=
maxmin fff ≤≤
4.Tìm góc xoay
α
∆
đ thu đ c sóng đi n t có b c sóng ể ượ ệ ừ ướ
λ
:
min
min
0
0
0180180 CC
CC
C
C
mã −
−
=
∆
∆
=∆
α
S u T mư ầ 4
V t lý l p 12 ậ ớ
VII.GIAO THOA ÁNH SÁNG:
•Cho trong kho ng L có N vân thì kho ng vân i b ng (N-1) lúc đó ả ả ằ
1−
=N
l
i
•
kix
a
D
i== ,
λ
1.Nh n bi t vân t i ( sáng ) b c m yậ ế ố ậ ấ :
i
x
k=
, k nguyên : sáng ; k l : t i vd: k=2,5 vân t i th 3ẻ ố ố ứ
2. Tìm s vân t i, sáng trong mi n giao thoa:ố ố ề
* Xét s kho ng vân ố ả trên n a mi n giao thoa ử ề có b r ng L thì: ề ộ
i
L
n=
= k( nguyên) + m( l )ẻ
* S vân trên ốn a mi nử ề giao thoa: Sáng k , T i : n u: m<0,5 có k ,n u m>0,5 có k+1ố ế ế
*S vân trên ốc mi nả ề giao thoa:
sáng: N= 2k+1 T i N’=2k N’=2(k+1)=2k +2ố
3.Có 2 ánh sáng đ n s c,tìm v trí trùng nhau:ơ ắ ị
xKKKK →→=
212211
,
λλ
4.Giao toa v i ánh sáng tr ng, tìm b c sóng ánh sáng đ n s c cho vân t i(sáng) t i 1 đi m M:ớ ắ ướ ơ ắ ố ạ ể
Gi i h : M sáng ả ệ
λ
λ
→= a
D
KxM
M t i ố
λ
λ
→+= a
D
KxM)
2
1
(
và
đotím
λλλ
≤≤
k⇒
( s vân)ố
5.Khi đ t b n m t song song ( e, n ) thì vân trung tâm ( h vân ) d ch chuy n: ặ ả ặ ệ ị ể
a
Dne
x)1(
0
−
=
VIII. HI N T NG QUANG ĐI N:Ệ ƯỢ Ệ
0
λ
hc
A=
v i 1ev= 1,6.10ớ-19 J ;
2
max0
2
1vmUe eh =
;
2
max0
2
1vmA
hc
e
+=
λ
1.Tìm v n t c e khi t i Anot: ậ ố ớ
AKe eUvmmv =− 2
max0
2
2
1
2
1
ho c ặ
AKhe eUUevm =−
2
2
1
2.Đ I= 0 thì ĐK là: ể
0<< hAK UU
tìm Uh, t đó l y ừ ấ
hAK UU >
3.Tìm s e trong 1s: ố q= ne =Ibht = Ibh t đó suy ra nừ
e
Ibh
=
s photon trong 1s N=ố
hc
P
λ
Hi u su t ệ ấ
N
n
H=
4.Tìm Vma x c a t m KL ( qu c u ) khi đ c chi u sáng:ủ ấ ả ầ ượ ế
2
max0max 2
1vmeV e
=
,
n u n i đ t ế ố ấ
R
V
R
U
Imax
max ==
5.Tia R n ghen: ơ
h
eU
f=
max
;
eU
hc
=
min
λ
S u T mư ầ 5