Lâm Hữu Minh - sherlockttmt@gmail.com
1
CÔNG THỨC VẬT LÝ TRỌNG TÂM THI ĐH - CĐ
Định luật cơ bản của ghi nhớ: Dành thời gian ngồi nhìn 1 vấn đề cần ghi nhớ để tìm ra (hoặc
tìm cách áp dụng) 1 kĩ thuật ghi nhớ nào đó chính là cách ghi nhớ vấn đề tự nhiên nhất, dù có tìm
ra (hay áp dụng) kĩ thuật được hay không.
Nguyên lí ghi nhớ công thức bằng âm thanh: Nghe (phát âm) nhiều về hình thức công thức sẽ
tạo âm điệu riêng cho công thức trong cảm nhận, do đó chỉ có thể phát âm để viết ra công thức.
Các bước ghi nhớ công thức bằng ý nghĩa tự nhiên:
_ Quan sát công thức để tìm ra sự đặc biệt riêng trong hình thức của nó (sự tương tự của nó với
một sự vật, một nguyên lí hiển nhiên, các kí tự chung của 2 vế, liên hệ với tên gọi, …). Khi cần
phân biệt 2 công thức, thường tìm sự khác biệt về độ dài, rộng, phức tạp, liên hệ tên gọi,…
_ Xây dựng một suy luận hoàn chỉnh (không nhất thiết phải có lời đầy đủ) để suy ra công thức từ
1 yếu tố nhỏ và các ý nghĩa tự nhiên đã gán.
_ Tập nhớ lại công thức từ những lời suy luận đã gán đến khi không còn nhầm lẫn giữa các suy
luận của mỗi công thức.
Cơ sở của cách thức này: não người dễ nhớ những thứ gần gũi với cuộc sống, những thứ có sự
logic chặt chẽ về hình thức, sinh động, trong khi đó công thức thường rắc rối mà khô khan, hình
thức không logic, xa rời đời sống.
Ở đây, cách ghi nhớ in nghiêng đặt trong ngoặc, không ghi tức dễ học thuộc. Ngoài ra mỗi người
có một lối tư duy khác nhau nên có thể tự sáng tạo ra những cách ghi nhớ khác cho riêng mình.
I. Công thức chung
x = f(t)
v = x’
a = v’ = x”; F = ma; 2 2
1 1
W ; W
2 2
d t
mv kx mgh
Chuyển động tròn đều:
2
;
ht
v
a v R
R
Bản chất của CTĐLTG (công thức độc lập thời gian): 2 2
sin ( ) cos ( ) 1
t t
CTXX (công thức xấp xỉ):
2
10 sin tg cos 1
2
o
2
(2 1)
(2 1)
2
k
k nguoc ph
cùng pha
vuông ph
k
a
a
Các hằng số lấy từ bảng const của MTBT, tự làm tròn theo hằng số trong SGK
II. Dao động cơ - điều hoà
cos( )x A t
; max
(biên độ); 2
max
a
(biên độ); số dao động trong :
t
t N
T
Tại 1 thời điểm: (li độ)22
2
v
(biên độ)2 (Suy từ CTĐLTG)
Lâm Hữu Minh - sherlockttmt@gmail.com
2
max min
: 2 sin ; 2 1 cos
2 2 2
T
Khi t S A S A
(vẽ đường tròn lượng giác)
Quãng đường đi được trong
2 2
1 1
2 1
: | | sin( )
t t
t t
t t t S v dt A t dt
(Coi như
2
2
1
1
2 1
'
t
t
t
t
S x x x x dt
)
Tổng hợp dao động:
2 2
1 2 1 2
1 1 2 2
1 1 2 2
2 cos
sin sin
cos cos
A A A A A
A A
tg A A
(dựa vào
sin
cos
tg và từ “tổng hợp”)
2 dao động có cùng A gặp nhau lần đầu khi
1 2
1 2
t
1. Con lắc lò xo
Khi đặt xiên 1 góc
so với mp ngang, ở VTCB: 0
sin
lmg
k
(vẽ hình)
1 1
2 2
1 2 1 2
2 2
( )
có có
c
m T
m m T T T
Tóm
(định lí Pitago và “m1 + m2”)
2 2
1 2 2 2
2 1 1 1
T f k g
T f k g
(dễ suy luận)
0 0
0 min
0
( ) ( )
( ) 0 ( )
dh dh
k l A A l
F k l x F A l
(vẽ hình); ph
F kx
Xảy ra cộng hưởng khi con lac ngoai luc
S
T T
v
(
S
: quãng đường giữa 2 lần liên tiếp bị ngoại lực; v:
vận tốc hệ) (bản chất là
S
t
v
)
Ghép lò xo:
_ Nối tiếp:
1 2
1 1 1
k k k
khi cùng treo vật m:
2 2 2
1 2
T T T
(thực ra 2 công thức là 1)
_ Song song: 1 2
k k k
khi cùng treo vật m:
2 2 2
1 2
1 1 1
T T T
(như trên)
(vẽ hình: nhìn thấy ghép song song khó đứt hơn
ghép song song cứng hơn. Ghép nối tiếp dài
hơn
công thức nối tiếp cồng kềnh hơn. Tưởng tượng thực tế: ghép song song là chập 2 lò xo
thành 1)
Lâm Hữu Minh - sherlockttmt@gmail.com
3
Nhốt thế năng khi vật có li độ xo:
( ) 1
2 2
2 1
0
W
W
'
t bi nhot
t
l
l
l l
A A x
l l
( 0
1 2
x
l l l
) (
1 1 2 2
W W W
'
sau truoc bi nhot
Al k l k
)
Va chạm mềm: 1
( )mv Mv m M V
, nếu m được ném xuống với v0 thì 2
1 0
2v v gh
(vì 2 2
1 0
2v v gh
)
Va chạm đàn hồi:
1 2 1
1
1 2
1 1 1 1 2 2
2 2 2
1 1 1 1 2 2 1 1
2
1 2
( )
'
' '
' ' 2
'
m m v
v
m m
m v m v m v
m v m v m v
m v
v
m m
(nhớ 1 công thức suy ra
công thức còn lại, còn dựa vào
1 1 2
1 2 1 2 1
1 2 '
2 ' 2
có
c
v m m
m m m v ó m
Vật m1, m2 dao động không rời nhau
max
A A
:
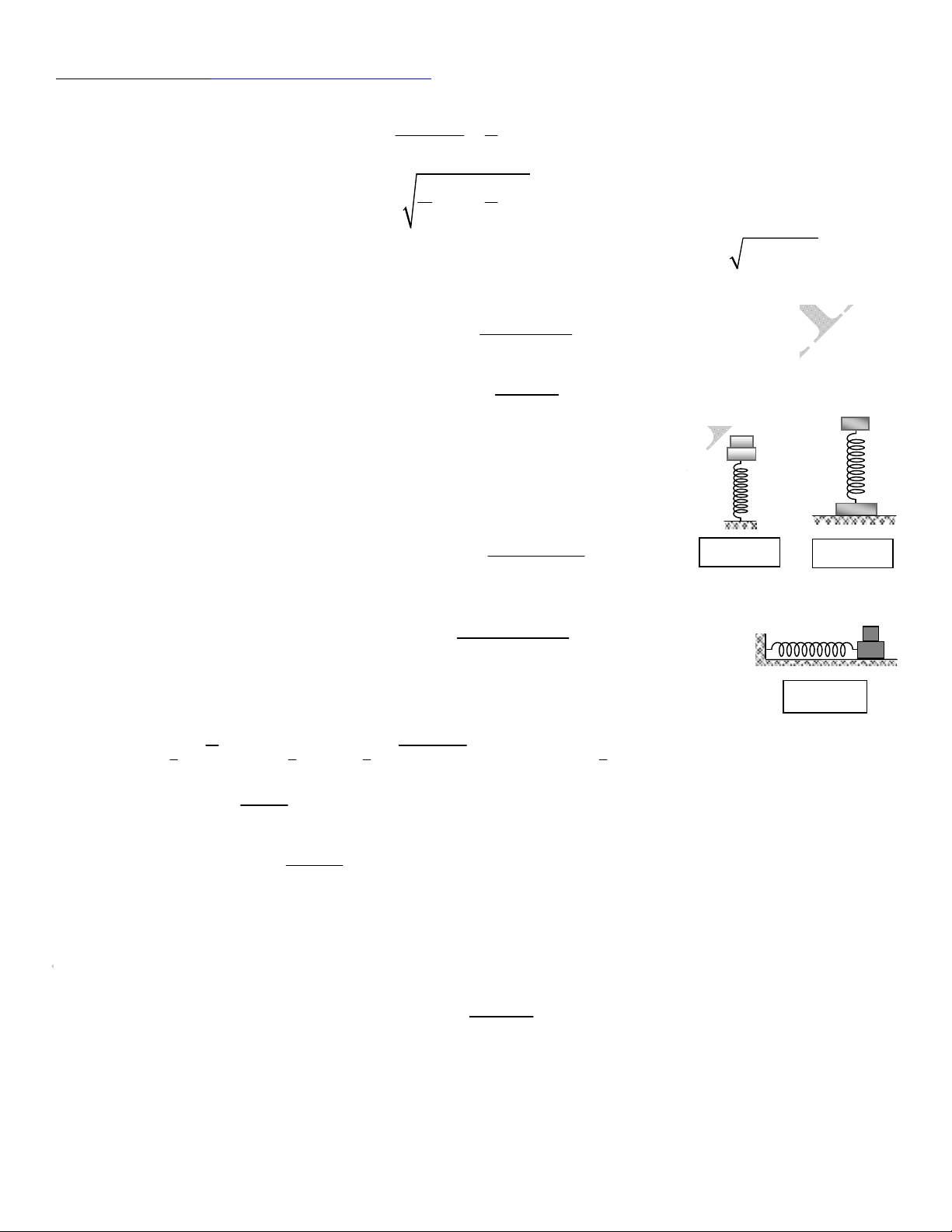
_ Với dao động thẳng đứng: 1 2
max max
( )
dh
m m g
F P A
k
(hình 1;
2)
_ Với dao động ngang: 1 2
max max
( )
dh ms
m m g
F F A
k
(hình 3)
(nhớ bản chất là 2 lực phải cân bằng)
Dao động tắt dần:
2 2
( )
2
2 2 2 2
2
12
2
ngoai luc
ngoai luc T
T T T T
F
F W m A A A A
m
(hiển nhiên)
số dao động
( )T
A
NA
thời gian dao động:
t NT
(vì coi T không đổi)
_ Tổng quãng đường:
ngoai luc
W
SF
(Với con lắc lò xo: 2
;
ngoai luc ms
F F mg m k
)
(nguyên lí: toàn bộ cơ năng chuyển thành công của ngoại lực để dừng lại:
ngoai luc ngoai luc
W A F S
)
_ Biên độ còn lại sau n dao động: n
A A n A
(hiển nhiên)
_ Vận tốc max:
max 0
' ( )v A A x
tại 0
ngoai luc
F
x
k
(nguyên lí:
max
v
tại VTCB, khi
0
ngoai luc đh
F F kx
)
k
m1
m2
Hình 1
m
2
m
1
k
Hình 2
Hình 3
m1
k
m2
Lâm Hữu Minh - sherlockttmt@gmail.com
4
_ Số lần qua vị trí lò xo không biến dạng: 0
2
T
A
NA
(giống công thức tính số dao động
nhưng là số lần nên có “[ ]”, và mỗi
2
T
qua vị trí này 1 lần)
Trạng thái lò xo lúc dừng khi ban đầu kích thích bằng cách:
+ Kéo dãn, là: dãn nếu N0 chẵn, nén nếu N0 lẻ
+ Nén lại, là: nén nếu N0 chẵn, dãn nếu N0 lẻ
(do số “chẵn” đẹp hơn số “lẻ” nên “N0 chẵn” luôn ưu tiên có trạng thái giống kích thích ban
đầu)
_ Vật dừng lại tại vị trí cách vị trí lò xo không biến dạng 1 đoạn:
2
2
T
T
x A n A
(
2
:
T
n
số khoảng thời gian
2
T
thực hiện được):
+ 0
2
2
5
T
T
A
n N A
+ 0
2
2
1 5
T
T
A
n N A
(Tưởng tượng thực tế)
Dao động duy trì: năng lượng cần cung cấp trong 1T:
2 2
( )
1
( ' )
2
T
k A A
W
E
T T

(Nhớ là: độ giảm năng lượng trong 1T)
Tổng năng lượng cung cấp:
dao dong
W
Et
2. Con lắc đơn
0
2 (cos cos )
v gl
(học thuộc); lực căng
0
(3cos 2cos )R mg
(nhớ “mg” vì R do P,
vẽ hình suy ra)
2 2
0
0
2 2
0
( )
10 3
12
v gl
mg
(từ CTXX);
2 2
2
sin
t
t n
n
tiêp tuyên
huong tâm
a g
a a a
v
al
2
0
1
2
W mgl
(suy từ W của S0)
Lâm Hữu Minh - sherlockttmt@gmail.com
5
1 2
1 2
T T
T T
chu kì trùng phùng
1 2
( 1)t n T nT
(n: số dao động của T2) (nhớ dạng 1
2
1
T n
T n
)
Lắc dao động trong ngoại lực
F
(gây gia tốc
a
) có phương:
_ Thẳng đứng:
'g g a
_ Ngang:
2 2
; '
a
tg g a g
g
(vẽ hình)
Biến thiên T:
0 0 0
2 2 2 2
o
T t h d l g
T R R l g
(
o
t
: nhiệt độ; h: độ cao; d: độ sâu)
(tổng quát:
0
T
T
(trạng thái) = (trạng thái sau) – (trạng thái trước))
Lượng thời gian đã bị sai sau khoảng thời gian
0 0
0
:T
t t t
T
(nhớ bản chất
0
%
sai
t T t
là công thức tính x
%
của y ở cấp tiểu học với
%sai
T
là của 1To)
Lắc vướng đinh:
1 2
2
T T
T
(T1: khi chưa bị mắc đinh; T2: khi bị mắc đinh) (vẽ hình)
Lắc va chạm mặt phẳng xiên góc
so với phương thẳng đứng: 02
2
T
T t
với
0
arcsin
t
(vẽ hình, dùng đường tròn lượng giác với biên độ
0
, li độ
)
Khi mặt phẳng thẳng đứng:
0
2
T
T
3. Năng lượng
2
1
W
2
tm
(biên độ)22
cos ( )
t
; 2
1
W
2
dm
(biên độ)22
sin ( )
t
(suy từ công thức
chung)
Các W dao động với
2
W A
f f
(hạ bậc sin2, cos2, dễ thuộc)
W W
d t
n
tại
1
A
x
n
(từ
max
W W W W
d t t
)
III. Sóng cơ
1. Đại cương
Nguồn tại O
sóng tại M: 2
cos cos( )
M
d
u A t A t
(nếu giữa M, N với
MN d
thì coi 1 điểm là nguồn)