
1
UBND THÀNH PH H CHÍ MINHỐ Ố Đ C NG CHI TI T H C PH NỀ ƯƠ Ế Ọ Ầ
TR NG ĐI H C SÀI GÒNƯỜ Ạ Ọ MÔN CHUNG C P Đ 4Ấ Ộ
H C PH NỌ Ầ
GI I TÍCH 2Ả
1. Thông tin v h c ph nề ọ ầ
- Tên h c ph n: GI I TÍCH 2ọ ầ Ả
- Mã h c ph n: 864006ọ ầ
- S tín ch : 3ố ỉ
- S ti t (lí thuy t, bài t p, th o lu n, th c hành): 45 (45; 0; 0; 0)ố ế ế ậ ả ậ ự
- Trình đ đào t o: đi h cộ ạ ạ ọ
- Đi u ki n đ h c h c ph n:ề ệ ể ọ ọ ầ
+ Đòi h i h c ph n h c tr c: 864005_Gi i tích 1ỏ ọ ầ ọ ướ ả
+ Đòi h i h c ph n h c song hành: khôngỏ ọ ầ ọ
+ Sĩ s sinh viên t i đa: 60ố ố
2. B môn ph trách gi ng d y ộ ụ ả ạ
B môn Gi i tích khoa Toán - ng d ngộ ả Ứ ụ
3. Mô t h c ph nả ọ ầ
Cung c p cho ng i h c phép tính vi phân, tích phân c a hàm nhi u bi nấ ườ ọ ủ ề ế
và ph ng trình, h ph ng trình vi phân v i các n i dung sau:ươ ệ ươ ớ ộ
- Phép tính vi phân c a hàm nhi u bi n: gi i h n, liên t c, đo hàm riêng, viủ ề ế ớ ạ ụ ạ
phân toàn ph n và các ng d ng.ầ ứ ụ
- Phép tính tích phân c a hàm nhi u bi n: Tích phân ph thu c tham s . Tíchủ ề ế ụ ộ ố
phân kép. Tích phân b i. Tích phân đng, tích phân m t và các ng d ng.ộ ườ ặ ứ ụ
- Ph ng trình và h ph ng trình vi phân.ươ ệ ươ
4. M c tiêu h c ph nụ ọ ầ
4.1. V ki n th cề ế ứ
- Trang b cho sinh viên nh ng ki n th c c b n v phép tính vi tích phânị ữ ế ứ ơ ả ề
c a hàm nhi u bi n làm n n t ng đ h c t p ti p các môn v t lý, xác su tủ ề ế ề ả ể ọ ậ ế ậ ấ
th ng kê, toán k thu t và các môn chuyên ngành khác. ố ỹ ậ
- G m các n i dung chính: ồ ộ
+ Phép tính vi phân c a hàm nhi u bi n. ủ ề ế
2
+ Tích phân c a hàm nhi u bi n: Tích phân ph thu c tham s . Tích phânủ ề ế ụ ộ ố
b i. Tích phân đng, tích phân m t và các ng d ng. ộ ườ ặ ứ ụ
+ Ph ng trình và h ph ng trình vi phân.ươ ệ ươ
4.2. V kĩ năngề
- Thông qua môn Gi i tích 2ả có th rèn luy n cho sinh viên các k năng sauể ệ ỹ
- Có các k năng tính toán v phép tính vi phân c a hàm nhi u bi n s : Cácỹ ề ủ ề ế ố
phép tính đo hàm, gradient, tích phân hàm nhi u bi n s . ạ ề ế ố
- Có k năng gi i ph ng trình vi phân c p 1, 2, h ph ng trình vi phân. ỹ ả ươ ấ ệ ươ
- Có k năng liên h các ki n th c toán h c vào các v n đ c a V t lý vàỹ ệ ế ứ ọ ấ ề ủ ậ
các ngành khoa h c công ngh khác.ọ ệ
- ng d ng công c gi i tích đ h c t p, nghiên c u các v n đ chuyên mônỨ ụ ụ ả ể ọ ậ ứ ấ ề
c a mình.ủ
4.3. V thái đề ộ
- Nghiêm túc, chu n b bài tr c khi đn l p, tích c c nghe gi ng trên l p.ẩ ị ướ ế ớ ự ả ớ
Có ý th c rèn luy n các k năng trên.ứ ệ ỹ
- Làm đy đ các bài t p, bài ki m tra và bài t p l n.ầ ủ ậ ể ậ ớ
5. N i dung và k ho ch d y h c h c ph nộ ế ạ ạ ọ ọ ầ
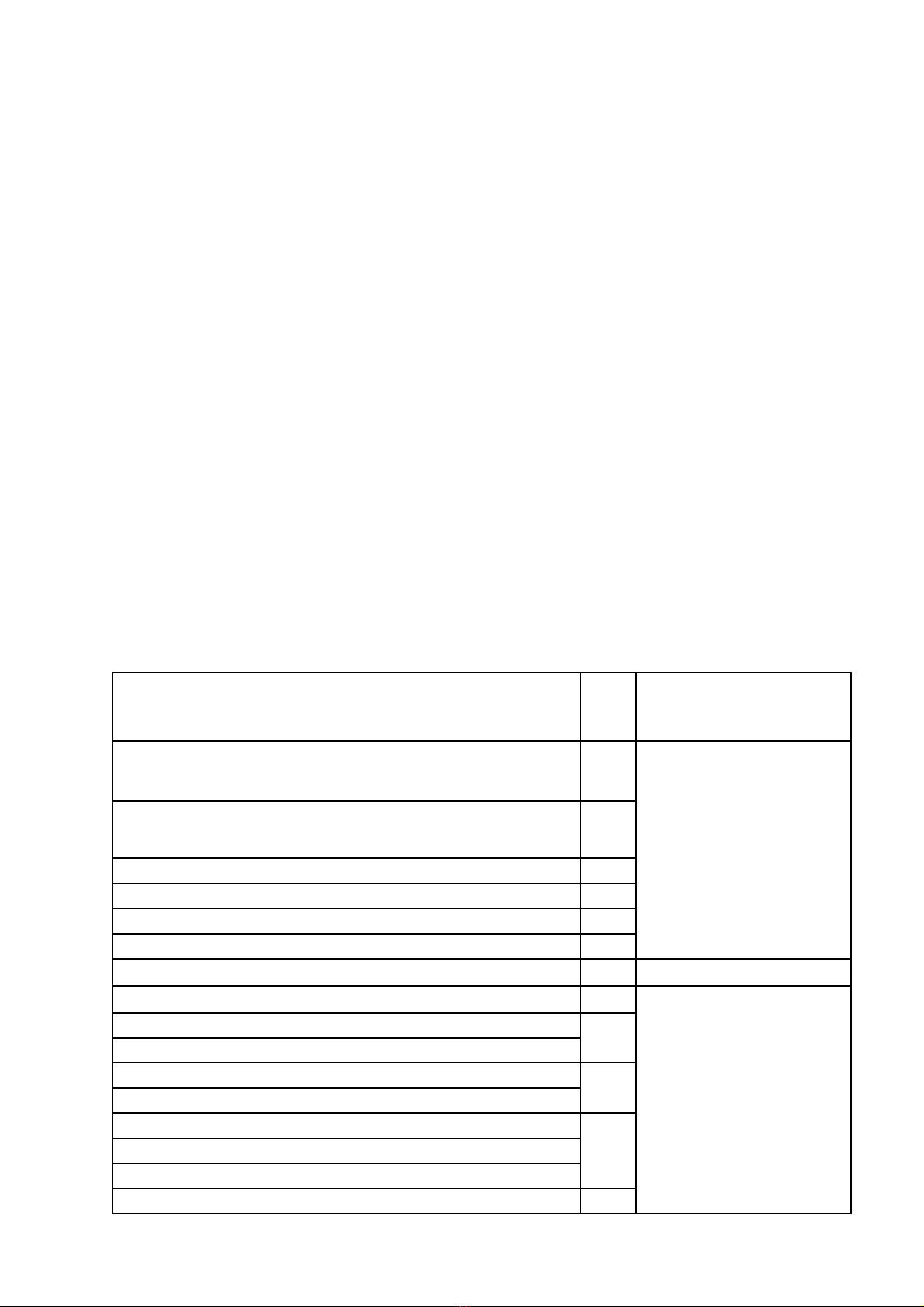
N i dung chi ti t c a h c ph nộ ế ủ ọ ầ Số
ti tế
Hình th c t ch c,ứ ổ ứ
ph ng pháp d y - h cươ ạ ọ
và ki m tra, đánh giáể
Ch ng 1:PHÉP TÍNH VI PHÂN HÀM NHI Uươ Ề
BI NẾ12
1.1 Không gian
n
ᄀ
. Khái ni m kho ng cách, lân c n,ệ ả ậ
mi nề2
1.2 Gi i h n - S liên t c c a hàm nhi u ớ ạ ự ụ ủ ề bi n sế ố 2
1.3 Đo hàm riêng và vi phân toàn ph nạ ầ 2
1.4 Công th c Taylor c a hàm hai bi n. C c tr ứ ủ ế ự ị 2
1.5 Tr ng vô h ng, Tr ng vect , Rôta, Diveườ ướ ườ ơ 2
1.6 Bài t pậ2
Ch ng 2. TÍCH PHÂN B Iươ Ộ 11
2.1 Tích phân xác đnh ph thu c tham sị ụ ộ ố 2
2.2 Tích phân suy r ng ph thu c tham sộ ụ ộ ố
2.3 Đnh nghĩa tích phân kép. Cách tính tích phân kép.ị2
2.4 Tính tích phân kép theo t a đ c c ọ ộ ự
2.5 Đnh nghĩa tích phân b i 3.ị ộ 2
2.6 Cách tính tích phân b i 3. Đi bi n s . ộ ổ ế ố
2.7 Tính tích phân b i 3 theo t a đ tr , t a đ c u ộ ọ ộ ụ ọ ộ ầ
2.8 M t vài ng d ng c a tích phân b i ộ ứ ụ ủ ộ 2

3
2.9 Bài t p ậ1
2.10 Ki m tra gi a k ể ữ ỳ 2
CH NG 3. TÍCH PHÂN ĐNG – TICHƯƠ ƯỜ
PHÂN MĂT10
3.1 Khái ni m tích phân đng lo i 1, cách tính tíchệ ườ ạ
phân đng lo i 1.ườ ạ 1
3.2 Khái ni m tích phân đng lo i 2, cách tính tíchệ ườ ạ
phân đng lo i 2.ườ ạ 2
3.3 Công th c Green và đnh lý 4 m nh đ t ngứ ị ệ ề ươ
đng.ươ
3.4 Đi u ki n tích phân đng không ph thu cề ệ ườ ụ ộ
đng đi. ườ 1
3.5 ng d ng c a tích phân đng lo i 1, lo i 2Ứ ụ ủ ườ ạ ạ 3
3.4 Khái ni m tích phân m t lo i 1, cách tính tíchệ ặ ạ
phân m t lo i 1ặ ạ
13.5 M t đnh h ng. Khái ni m tích phân m t lo i 2,ặ ị ướ ệ ặ ạ
cách tính tích phân m t lo i 2ặ ạ
3.6 Công th c Stokes, Công th c Ostrogradskyứ ứ
3.7 Bài t pậ2
CH NG 4. PH NG TRINH VI PHÂN VÀ HƯƠ ƯƠ Ệ
PH NG TRÌNH VI PHÂNƯƠ 10
4.1 Khái ni m chung v ph ng trình vi phân . ệ ề ươ 2
4.2 Đnh nghĩa ph ng trình vi phân c p 1 và đnh lýị ươ ấ ị
t n t i nghi mồ ạ ệ
4.3 Các d ng ph ng trình vi phân c p 1 ạ ươ ấ 2
4.4 Đnh nghĩa ph ng trình vi phân c p 2ị ươ ấ
4.5 Ph ng trình vi phân tuy n tính c p 2. ươ ế ấ
2
4.6 Ph ng trình vi phân tuy n tính c p 2 v i h sươ ế ấ ớ ệ ố
h ngằ
4.7 Đnh nghĩa h ph ng trình vi phân. Ph ng phápị ệ ươ ươ
gi i.ả2
4.8 Hê ph ng trinh vi phân v i h s h ng) ươ ớ ệ ố ằ
4.9 Bài t pậ2
ÔN T P Ậ2
6. Tài li u h c t pệ ọ ậ
6.1. Tài li u chínhệ

4
1. Nguy n Đình Trí, ễToán h c cao c p t p 3ọ ấ ậ , NXB Giáo D c Vi t Nam 2007.ụ ệ
6.2. Tài li u khácệ
2. Đô Công Khanh, Nguyên Minh Hăng, Ngô Thu L ng (2006), ươ Toan cao câp –
Giai tich nhiêu biên , NXB ĐHQG Tp. HCM.
3. Đinh Th L c, Ph m Huy Đi n, T Duy Ph ng (2002), ế ụ ạ ể ạ ượ Gi i tích các hàmả
nhi u bi n: Nh ng nguyên lý c b n và tính toán th c hànhề ế ữ ơ ả ự , NXB ĐHQG Hà
N i.ộ
4. James Stewart (2011), Multivariable Calculus, 7th Edition, Brooks Cole.
5. Ph m Hoàng Quân (2011), ạGiáo trình Gi i tích 3, 4ả, Khoa Toán- ng d ng,Ứ ụ
ĐH Sài Gòn.
6. Phan Qu c Khánh (1998), ốPhép tính vi tích phân (t p 2)ậ, NXB Giáo D c Vi tụ ệ
Nam.
7. Ph n m m hay công c h tr th c hành: MAPLE 17ầ ề ụ ỗ ợ ự
7. Ph ng pháp đánh giá h c ph nươ ọ ầ
7.1. Thang đi m: thang đi m 10, làm tròn đn ph n nguyênể ể ế ầ
7.2. S bài ki m tra quá trình (nhi u l n ho c m t l n ki m tra gi a kì): 1ố ể ề ầ ặ ộ ầ ể ữ
7.3. Hình th c thi k t thúc h c ph n: t lu n, đ đóng (thí sinh không đcứ ế ọ ầ ự ậ ề ượ
mang tài li u vào phòng thi), th i gian làm bài: 90 phút.ệ ờ
7.4. Các đi m quá trình và tr ng s /h s t ng ngể ọ ố ệ ố ươ ứ
- Đi m chuyên c n: h s 0.1;ể ầ ệ ố
- Đi m th c hành/bài t p: h s 0.0;ể ự ậ ệ ố
- Đi m th o lu n trên l p: h s 0.0;ể ả ậ ớ ệ ố
- Đi m trung bình c a các bài ki m tra quá trình: h s 0.3;ể ủ ể ệ ố
- Đi m thi k t thúc h c ph n (h s ph i l n h n ho c b ng 0.5): h s 0.6ể ế ọ ầ ệ ố ả ớ ơ ặ ằ ệ ố
7.5. Đi m h c ph n: là đi m trung bình chung c a các đi m nêu m c 7.4ể ọ ầ ể ủ ể ở ụ
Thành ph H Chí Minh, ngày 20 tháng 04 năm 2016ố ồ
DUY TỆTR NG NGÀNH ƯỞ TR NG B MÔN ƯỞ Ộ NG I BIÊN SO NƯỜ Ạ
TS.Lê Minh Tri tếTS.Lê Minh Tu nấ


























