Tuyển tập Hội nghị Khoa học thường niên năm 2024. ISBN: 978-604-82-8175-5
101
ÁP DỤNG PHÉP PHÂN TÍCH TRỰC CHUẨN
GIẢI PHƯƠNG TRÌNH ĐỐI LƯU - KHUẾCH TÁN
Nguyễn Đức Hậu
Trường Đại học Thủy lợi, email: ndhau.dhtl@tlu.edu.vn
1. GIỚI THIỆU CHUNG
Phương pháp phân tích trực chuẩn theo giá
trị riêng (POD) được sử dụng đầu tiên trong
bài toán phân tích dữ liệu bởi Lumley [1]
năm 1967 để xác định cấu trúc của dòng chảy
rối. Phương pháp này được sử dụng để xấp xỉ
hệ phương trình Navier-Stokes nhằm xây
dựng lại và kiểm soát dòng chảy. Phương
pháp POD sẽ xác định một hệ sơ sở trực
chuẩn để xấp xỉ (một cách tối ưu) các dữ liệu
ban đầu là tập hợp rời rạc hoặc liên tục có cỡ
lớn [2, 3]. Trong bài báo này tác giả sử dụng
phương pháp POD nghiên cứu phương trình
đối lưu-khuếch tán một chiều.
2. PHƯƠNG PHÁP NGHIÊN CỨU
2.1. Phương pháp phân tích trực chuẩn
theo giá trị riêng (POD)
Tích trong của hai trường véc tơ u và v
được xác định như sau:

,: d

uv u vx, (1)
với chuẩn được xác định bởi:
:,
uuu.
Trung bình theo thời gian của đại lượng
f
trên khoảng thời gian T là:
0
1
:
T
f
fdt
T
. (2)
Trường vận tốc được phân tích thành:
 
0
,',ttux u x u x ,
ở đó:

1
', N
ii
i
tat
ux vx,
với

2
1
N
iiL
v là hệ cơ sở POD.
Ten sơ tương quan được xác định bởi:

(,) ' , ' ,ttRx
y
ux u
y
.
Bài toán xác định giá trị riêng i
và véc tơ
riêng i
u:

,iii
Rx
y
u
y
ux.
Ta có:
1
N
iijj
j
T
uv,
do đó:
 
11 1
NN N
jk ik j i i j j
jk j
QT T


vx vx,
ở đó ma trận Q được xác định bởi:
 

1
,
N
jk j m k m
m
Qatat
vv . (3)
Bài toán trở thành:

11
0
NN
jk ik i i j j
jk
QT T




 vx .
Dạng ma trận của bài toán là:
ii
i
Qt t .
Trực chuẩn hóa:
1
'
N
iijj
j
T
uv; 1
iu.
2.2. Xét phương trình đối lưu-khuếch tán
2
2
uu u
tx x



,
ở đó u là vận tốc, t là thời gian, 1/Re
.
Điều kiện biên tại 0
x
và
x
là:
0, cosut t,
và:
lim , 0
xuxt

.
Tuyển tập Hội nghị Khoa học thường niên năm 2024. ISBN: 978-604-82-8175-5
102
Bài toán trên có nghiệm là:

cos
x
ue xt
,
với:
2
22116 2
4

,
2
22116
4

.
3. KẾT QUẢ NGHIÊN CỨU
Nghiệm của phương trình đối lưu-khuếch
tán một chiều có thể biểu diễn dạng:
, cos . cos sin sin
xx
uxt te x te x




2
1
ii
i
atvx
,
ở đó:
1() cosat t, 2() sinat t, (4)
12
() cos , () sin .
xx
vx e xv x e x


 (5)
Xét trong chu kì 2T
và miền không
gian
0, . Tính toán ma trận Q trong
(3) nhờ các công thức (1) và (2), đối với các
hàm trong (4) và (5), và 2N, ta nhận được:

22
2
22
2
1
8






Q,
và các mod POD sau khi đã chuẩn hóa là:

1
22
2
cos sin ,
x
ux e
x
x







2
22
2
cos sin ,
x
ux e
x
x






các hệ số thời gian được xác định bởi:

122
22
2
4
sin cos ,
at
tt








222
22
2
4
sin cos .
at
tt







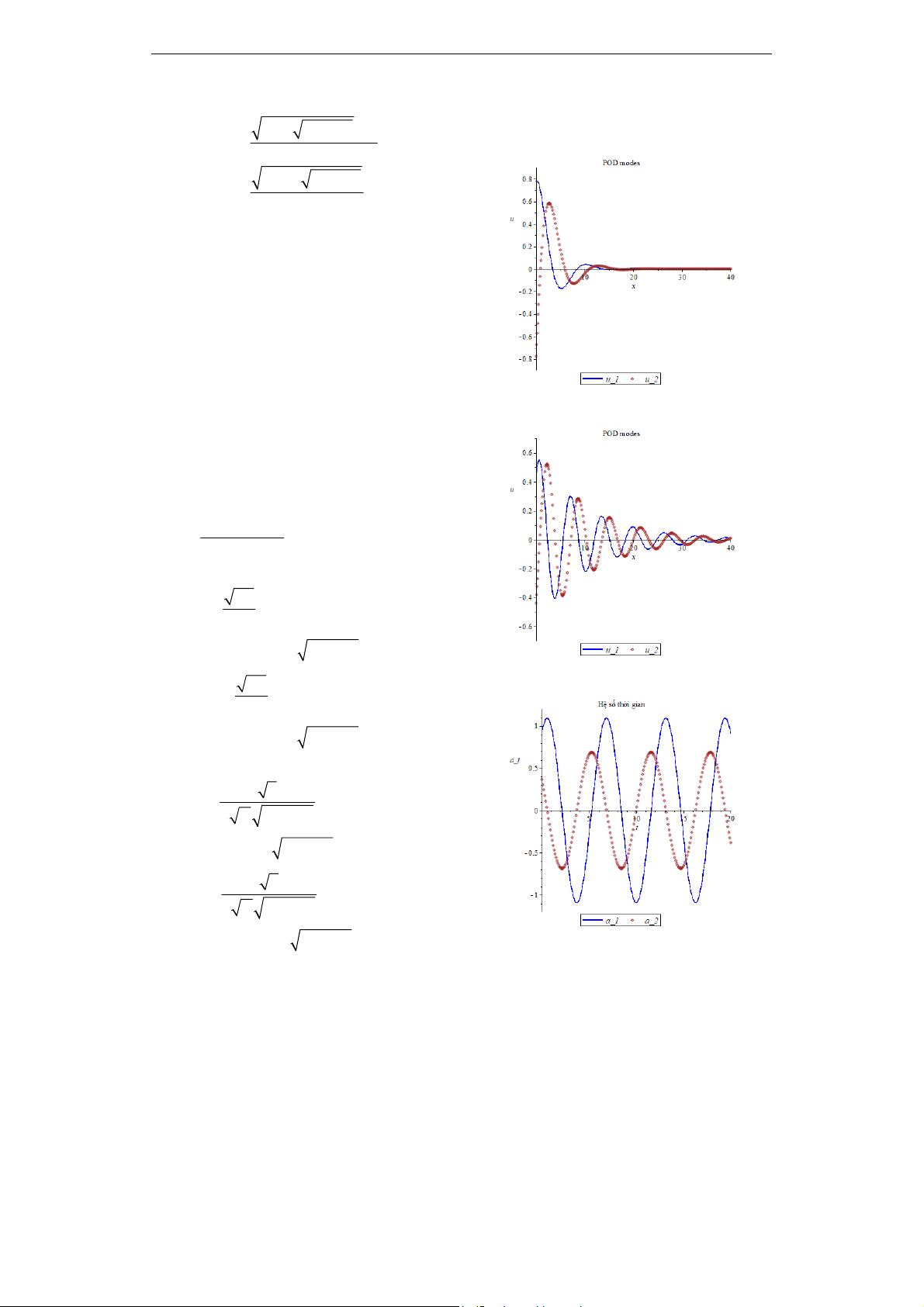
Trong các hình 1 và hình 2 biểu diễn hai
POD modes trong trường hợp
= 1 và
= 0.1.
Hình 3 và hình 4 biểu diễn hai hệ số thời gian
trong trường hợp
= 1 và
= 0.1.
Hình 1. POD mode trong trường hợp
= 1
Hình 2. POD mode trong trường hợp
= 0.1
Hình 3. Hệ số thời gian trong trường hợp
= 1
Tuyển tập Hội nghị Khoa học thường niên năm 2024. ISBN: 978-604-82-8175-5
103
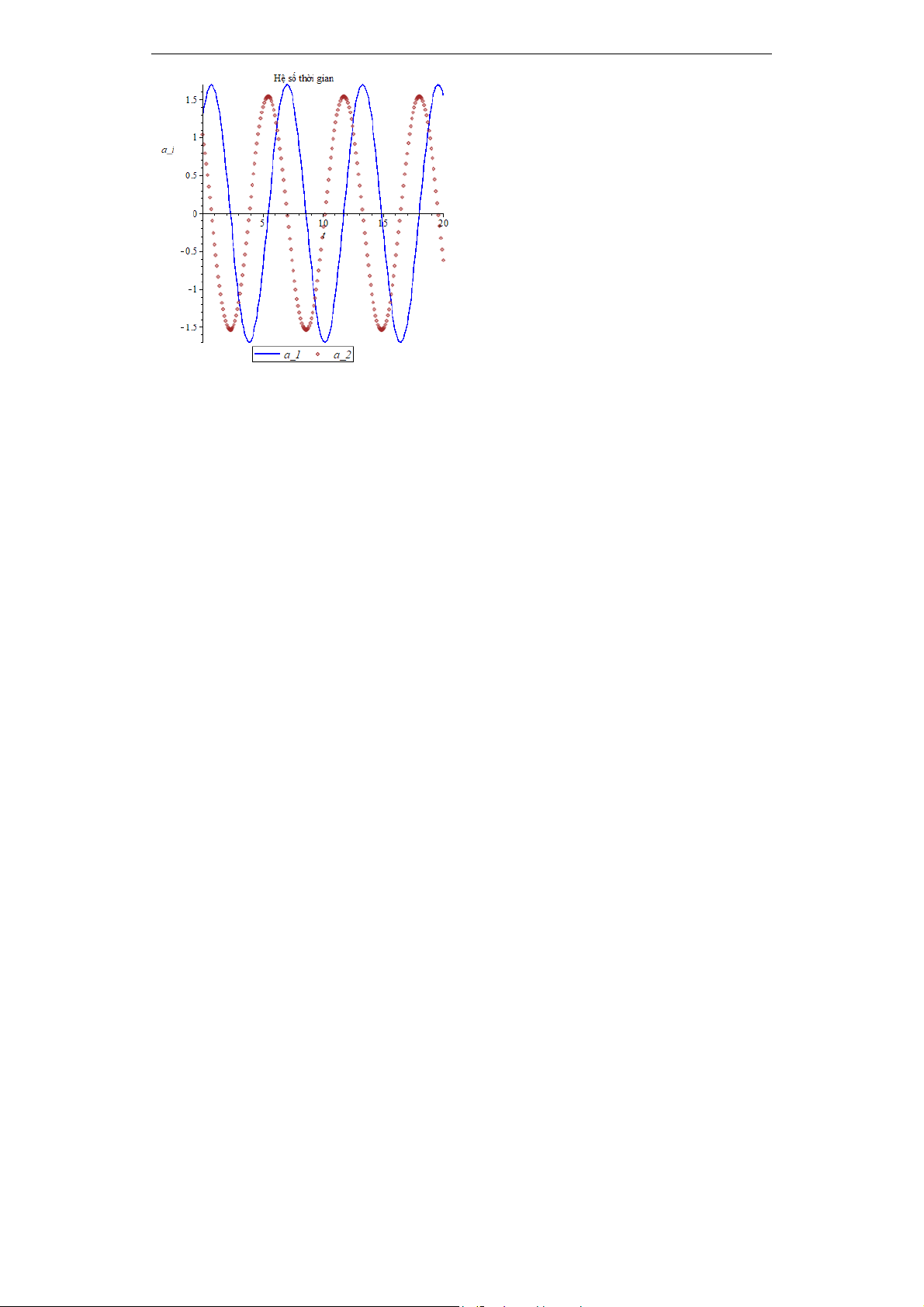
Hình 4. Hệ số thời gian trong trường hợp
= 0.1
4. KẾT LUẬN
Trong bài báo này tác giả sử dụng phương
pháp POD để nghiên cứu nghiệm của phương
trình đối lưu-khuếch tán trong trường hợp
một chiều. Hai mod POD sau khi đã chuẩn
hóa và hệ số thời gian đã được xác định.
5. TÀI LIỆU THAM KHẢO
[1] Lumley, J. L. (1967), The structure of
inhomogeneous turbulent flows,
Atmospheric turbulence and radio wave
propagation, Moscow : Nauka, 167-178.
[2] Nguyễn Đức Hậu (2023). Áp dụng phép
phân tích trực chuẩn phân tích dữ liệu trong
bài toán dòng chảy rối. Tuyển tập Hội nghị
Khoa học Thường niên năm 2023, tr. 84-86.
[3] Sirovich, L. (1987), Turbulence and the
dynamics of coherent structures, Quarterly
of Applied Mathematics, 5, 561-590.