


  !!"

#$%&'%()*+&,%!-.,/0
1$%2,3,4!567789:/0
;$%,%!-<&5=& >?73,
/0=>?
@,%!-!<&'%()*+/0A00
 !"#
B$??&(.!<$??
CD,%E.,$??F(.8(
CC8<5G,HI&J<K,I
C$? HLMJ<!<I8.%L
CN<EOP$F(.8(?QR SOP$

$%&
C@&,%!-!<PTU$
CB,%!-!<VWXTU$
DX?,Y??!5Z,SOP$??5G,TU$
'()(
$%,%!-!<&'%()*+[P$
1$%,%!-!<&'%()*+X\
;$%,%!-!<&'%()*+/]+
@$%,%!-!<&'%()*+$\]+

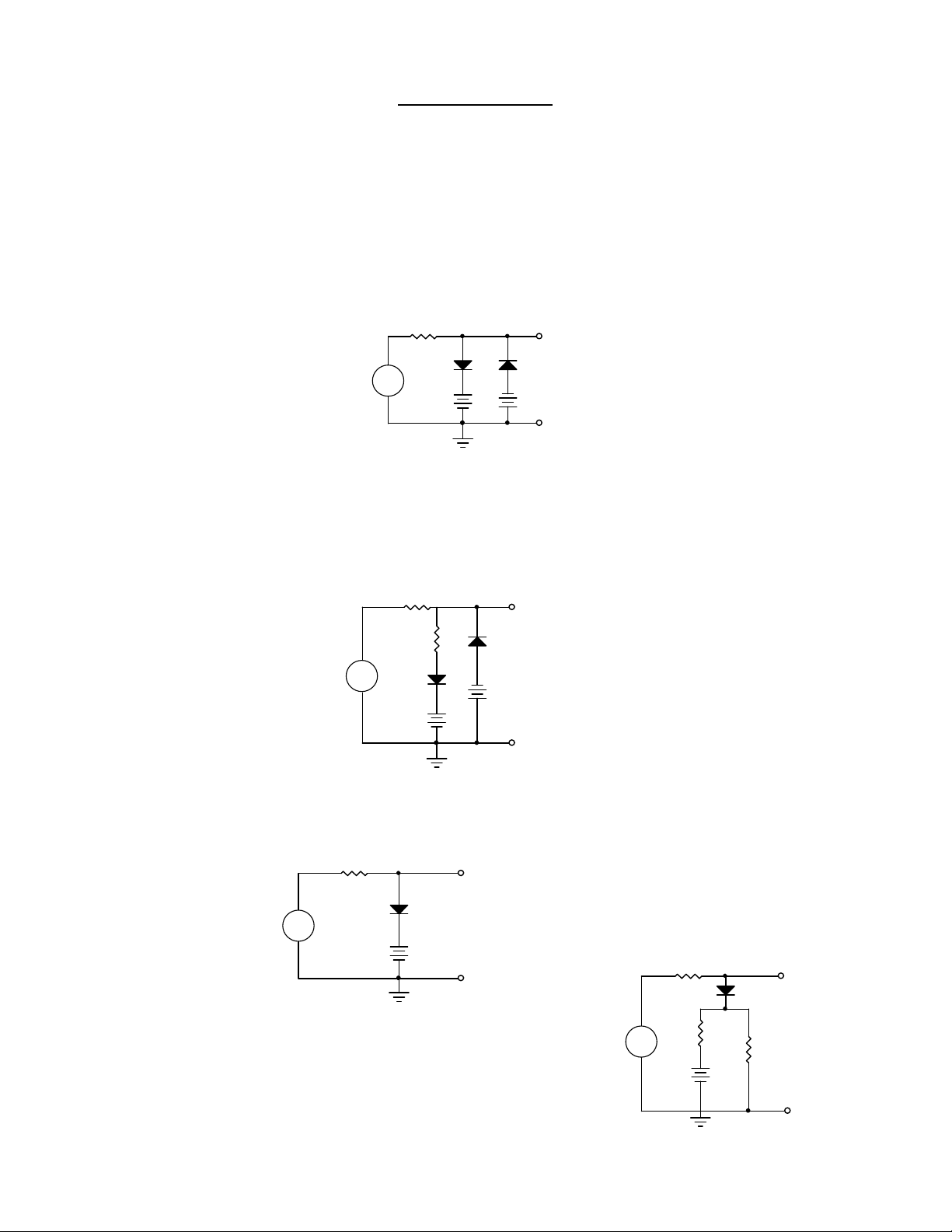
BÀI TP DIODE
Cho mch nh hình v xác nh in áp u ra
(
)
io vfv
=
1a. VEVEtvi6;8;sin10 21
=
=
=
ω
; Diode D1 và D2 là lý tng
1b. VEVEtvi4;2;sin5 21
=
=
=
ω
; Diode D1 và D2 có
Ω
=
=
10;7,0 DD RVU
1c. vi có dng xung tam giác biên  VEVEVUm5;3;8 21
=
=
=
;
Diode D1 và D2 là lý tng
1d. vi có dng xung vuông biên  VEVEVUm2;3;5 21
=
=
=
;
Diode D1 và D2
Ω
=
=
12;7,0 DD RVU
2a. VEVEtvi2;5;sin8 21
=
=
=
ω
; Diode D1 và D2 là lý tng
2b. VEVEtvi1;3;sin5 21
=
=
=
ω
; Diode D1 và D2 có
Ω
=
=
10;7,0 DD RVU
2c. vi có dng xung tam giác biên  VEVEVUm5;2;10 21
=
=
=
;
Diode D1 và D2 là lý tng
3a. VEtvi5;sin8
=
=
ω
; Diode D là lý tng
3b. VEtvi2;sin5
=
=
ω
; Diode D có
Ω
=
=
10;7,0 DD RVU
4a. VEtvi15;sin10
=
=
ω
; Diode D là lý tng
4b. VEtvi15;sin10
=
=
; Diode D có
Ω
=
=
10;7,0 DD RVU
+
+
~

\^CD8
/

/
C
U
C
U
+
~

\^C8
/
U
+
+
~

C8\
\C^C
8
/

/C
UC
U

\
^C
8
+
~

\C^C8
8\
/
U
5a. VEtvi5;sin10
=
=
ω
; Diode D là lý tng;
Ω
=
k
R
10
5b. VEtvi5;sin10
=
=
ω
; Diode D có
Ω
=
=
10;7,0 DD RVU ;
Ω
=
k
R
10
6a. Xác nh
(
)
tfvo
=
; bit tvRC i
sin20;
=
>>
; Diode D là lý tng
6b. Xác nh
(
)
tfvo
=
; bit
>>
RC
; vi có dng xung vuông biên  VUm10
=
;
Diode D là lý tng
BÀI TP BJT
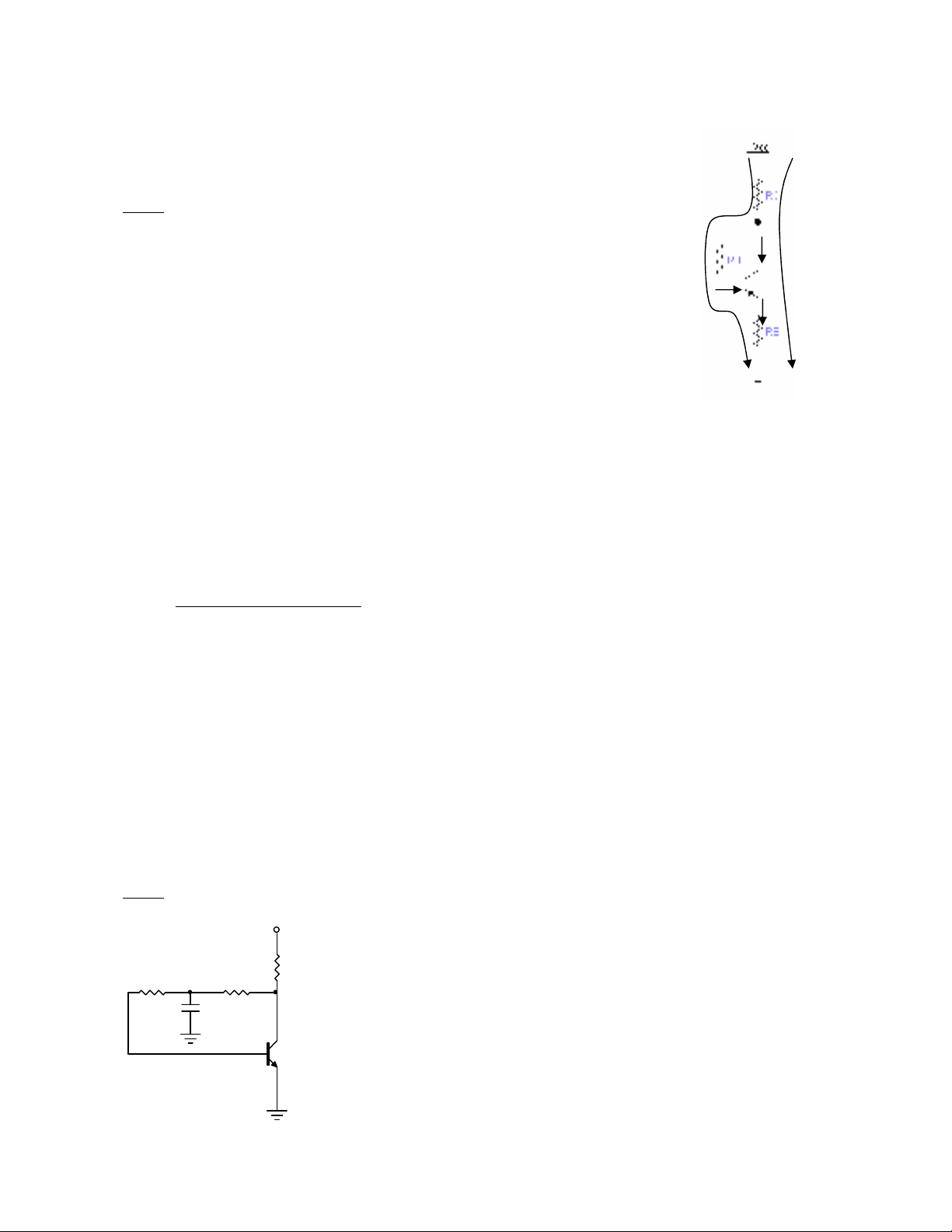
Bài 1. Cho mch (hình 1):
VCC=12V; UBEQ=0,7V; =100
RB= 100K; RC=1K; RE=500
Xác nh im công tác tnh và v ng ti tnh
Bài gii:
Áp dng nh lut Kirchhoff II
Vòng 1:
EEBEBBCC RIURIV ..
+
+
=
BCBE IIII )1(
β
+
=
+
=
hay:
(
)
EBBEBBCC RIURIV .1.
β
+
+
+
=
Vy:
~


/

R
D
+
E

~
+
E D
R
~

+
~
 \
/
U^#)

Vcc
RE
RC
RB
Hình 1
IB
IE
IC
1
2
( )
EB
BECC
BRR
UV
I.1
β
++
−
=
( )
A
RR
UV
I
EB
BEQCC
BQ
µ
β
56
.1 =
++
−
=
mAII BQCQ 6,556.100.
=
=
=
β
Vòng 2:
EECECCCC RIURIV ..
+
+
=
CE II
≈
nên:
(
)
ECCCECC RRIUV
+
+
=
.
hay:
(
)
ECCCCCE RRIVU
+
−
=
., ây chính là phơng trình ng ti tnh.
(
)
VRRIVU ECCQCCCEQ 6,3.
=
+
−
=
im làm vic tnh
(
)
CEQCQBQ UIIQ ,,
Bài 2. Cho mch (Hình 1)
VCC=9V; UBEQ=0,7V; =80;
RC=1,2K; RE=470;
Xác nh giá tr ca RB  im làm vic tnh Q nm chính gia ng ti tnh.
Phơng trình ng ti tnh:
(
)
ECCCCCE RRIVU
+
−
=
.
mA
RR
V
IU
EC
CC
CCE 4,5
47,02,1
9
0=
+
=
+
=→=
VVUI CCCEC 90
=
=
→
=
Vy:  im làm vic tnh Q nm chính gia ng ti tnh thì:
VU
A
I
ImAI
CEQ
C
BQC
5,4
7,337,2
=
==→=
µ
β
Áp dng nh lut Kirchhoff II cho vòng 1:
EEBEBBCC RIURIV ..
+
+
=
hay:
(
)
EBBEBBCC RIURIV .1.
β
+
+
+
=
Vy
Ω
=
kRB208
Bài 3. Cho mch (Hình 2)
VCC=6V; UBEQ=0,7V; =150
RB=1,5K; RC=1K; RE=1,8K
Xác nh im làm vic tnh Q và v ng ti tnh.
Áp dng nh lut Kirchhoff II:
Phơng trình u vào:
(
)
EEBEBBCCBCC RIURIRIIV ...
+
+
+
+
=
(
)
BECB IIII .1
β
+
=
=
+
Vy:
(
)
(
)
(
)
[
]
ECBBBEECEBEBBCC RRRIURRIURIV
+
+
+
+
=
+
+
+
=
.1...
β
1
>>
β
( )( )
A
RRR
UV
I
ECB
BEQCC
BQ
µ
β
5,12
.1 =
+++
−
=
mAII BQCQ 87,110.5,12.150. 3=== −
β
Phơng trình u ra:
(
)
ECCCEEECECBCCC RRIURIURIIV
+
+
≈
+
+
+
=
..).(
(
)
ECCCCCE RRIVU
+
−
=
., ây chính là phơng trình ng ti tnh.
Vy:
(
)
VRRIVU ECCQCCCEQ 8,0.
=
+
−
=
Bài 4. Cho mch (Hình 3)
VCC=9V; =100; UBEQ=0,7V
RC=1K; R1=1,8K;R2=22K
Xác nh im làm vic tnh Q và v ng ti tnh.
Bài gii:
Trong ch  tnh, t ngn thành phn mt chiu, b t.
a sơ  v dng ging bài 3: 21 RRRB
+
=
+Vcc
C1
Rc
R2
R1
Hình 3
Hình2
IC
IB
IE