1
Tran Quang Viet – FEEE – HCMUT Electromagnetics Field
Nguyên lý bức xạđiện từ& nguyên tốanten
Lecture 14
EE 2003: Trường điện từ
L.O.3.2 - Dùng nghiệm của phương trình D’Alembert để
giải thích nguyên lý bức xạ điên từ của nguyên tố anten
thẳng.
EE 2015 : Signals & Systems Tran Quang Viet – FEEE - HCMUT
Tran Quang Viet – FEEE – HCMUT Electromagnetics Field
Hiện tượng bức xạđiện từ
(t R/v)dV
1
(t)=
4 R
V
V

V
J(t R/v)dV
A(t)=
4 R
CuuDuongThanCong.com https://fb.com/tailieudientucntt
2
EE 2015 : Signals & Systems Tran Quang Viet – FEEE - HCMUT
Tran Quang Viet – FEEE – HCMUT Electromagnetics Field
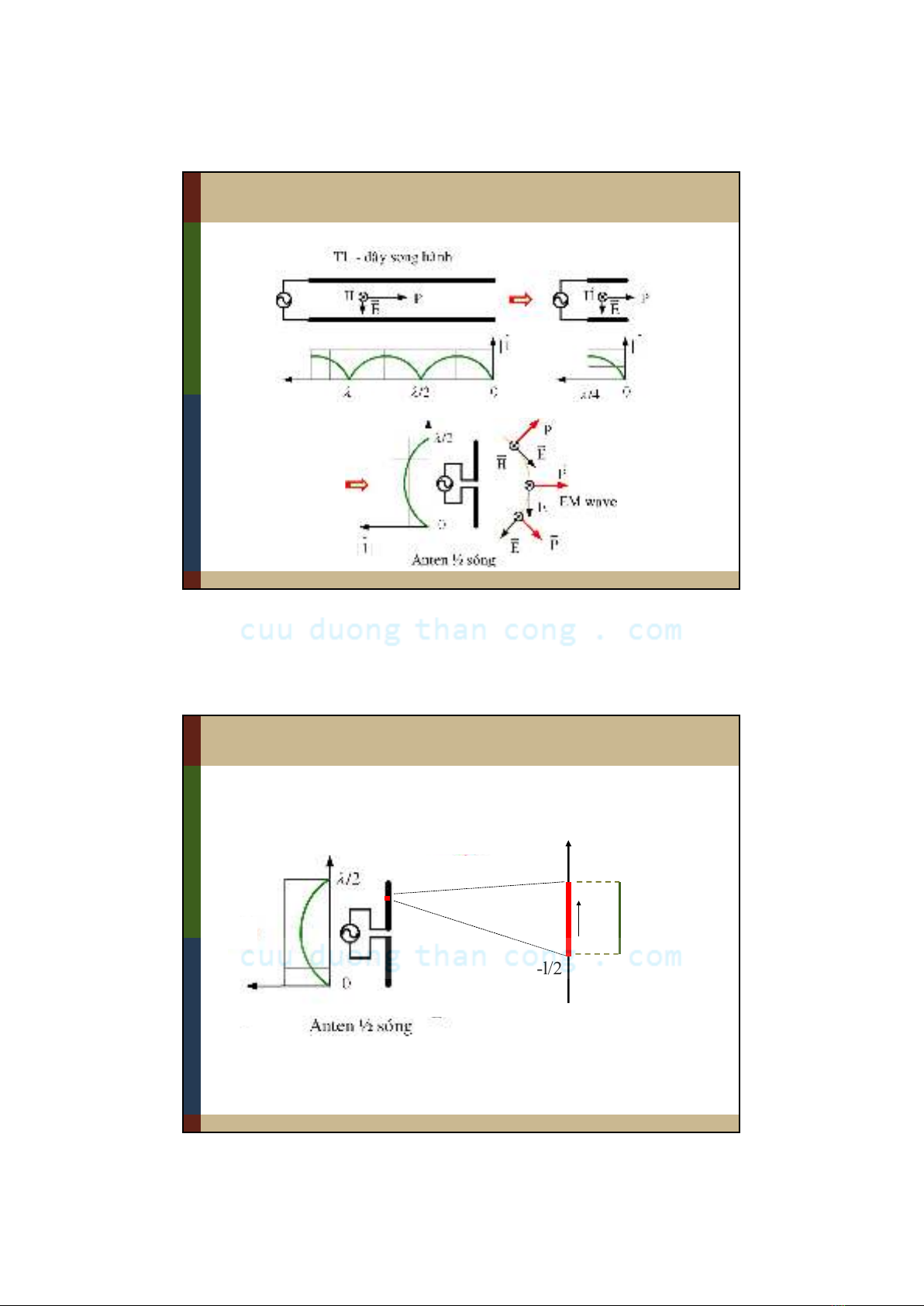
Giới thiệu anten ½ sóng
EE 2015 : Signals & Systems Tran Quang Viet – FEEE - HCMUT
Tran Quang Viet – FEEE – HCMUT Electromagnetics Field
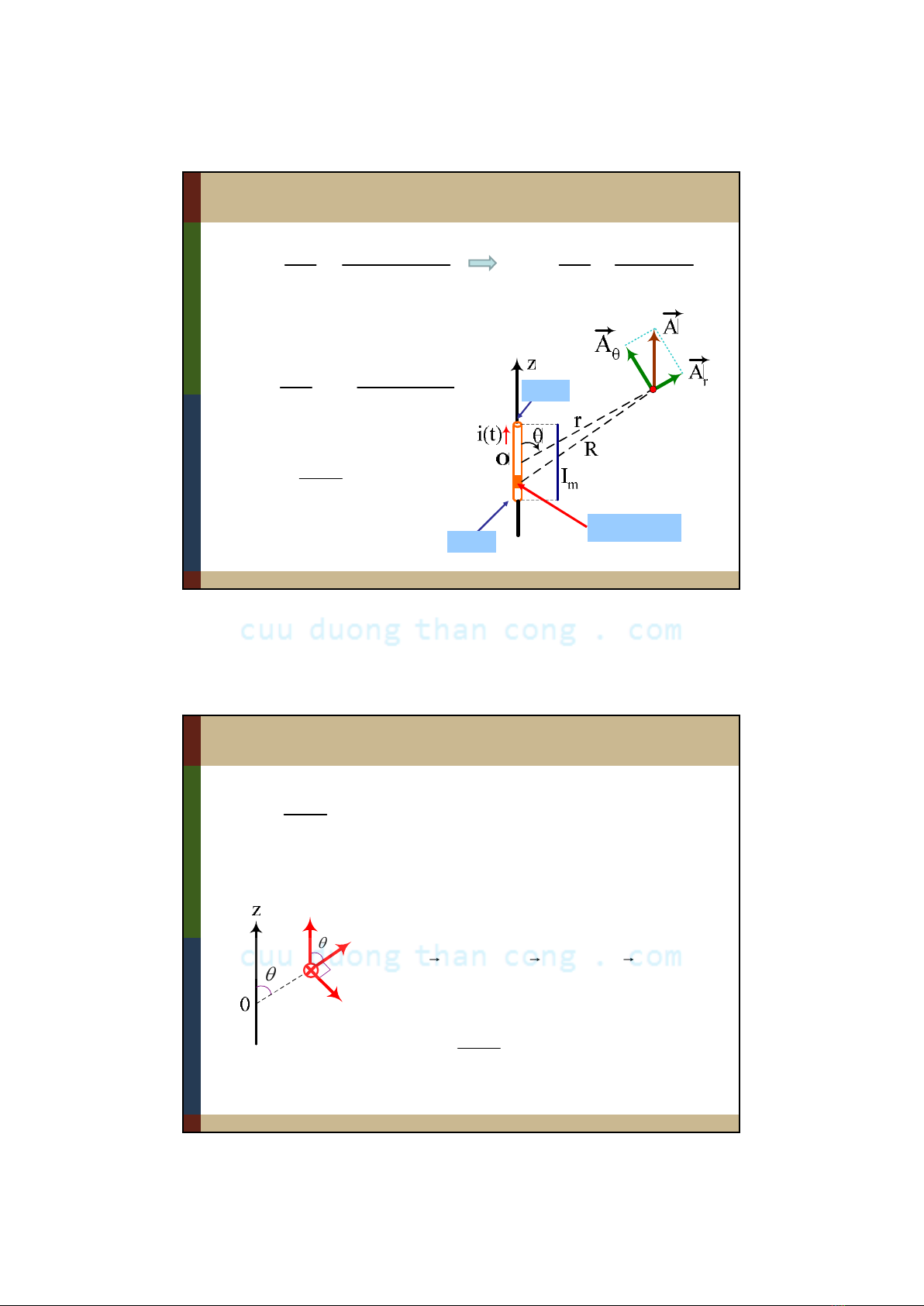
Giới thiệu nguyên tốanten thẳng
z
-l/2
+l/2
Im=const
l<</2
i(t)=Imcos(t+)
i(t)
CuuDuongThanCong.com https://fb.com/tailieudientucntt
3
EE 2015 : Signals & Systems Tran Quang Viet – FEEE - HCMUT
Tran Quang Viet – FEEE – HCMUT Electromagnetics Field
Tính thếvectơcủa nguyên tốanten thẳng
V
J(t-R/v)dV
A(t)=
4 R
'z
d dz a
/ 2
/ 2
/ 2
/ 2
'
-j
I e
A=
4 R
R
z
dz a
-j
I
A e
4
r
z
a
r
R
-j
L
Ie d
A=
4 R
EE 2015 : Signals & Systems Tran Quang Viet – FEEE - HCMUT
Tran Quang Viet – FEEE – HCMUT Electromagnetics Field
Tính thếvectơcủa nguyên tốanten thẳng
Biểu diễn thế vectơ trong hệ tọa độ cầu:
r
z
a
r
a
a
a
z r z r z z
a a a a a a a a a a
cos sin
z r
a a a
Icos sin
4
j r r
A e a a
r
-j
I
A e
4
r
z
a
r
CuuDuongThanCong.com https://fb.com/tailieudientucntt
4
EE 2015 : Signals & Systems Tran Quang Viet – FEEE - HCMUT
Tran Quang Viet – FEEE – HCMUT Electromagnetics Field
Tính trường từcủa nguyên tốanten thẳng
1
μ
H = rot A
2
-jβr
2 2
I β j 1
H = sin
θ + e a
4π βr β r
Icos sin
4
j r r
A e a a
r
EE 2015 : Signals & Systems Tran Quang Viet – FEEE - HCMUT
Tran Quang Viet – FEEE – HCMUT Electromagnetics Field
Tính trường điện của nguyên tốanten thẳng
2
-jβr
2 2
I β j 1
H = sin
θ + e a
4π βr β r
E =(1/j
ωε)rot H
3
-jβr r
2 2 3 3
3
-jβr
θ
2 2 3 3
jI β j 1
E =- cosθ + e a
2πωε β r β r
jI β 1 j 1
- sin
θ - + + e a
4πωε βr β r β r
CuuDuongThanCong.com https://fb.com/tailieudientucntt
5
EE 2015 : Signals & Systems Tran Quang Viet – FEEE - HCMUT
Tran Quang Viet – FEEE – HCMUT Electromagnetics Field
Trường ĐT trong miền gần của nguyên tốanten thẳng
Miền gần được định nghĩa là:
βr<<1 r<< /2
βr
2 2 3 3
1 1 1 ; ~1
βr β r β r
j
e
Với định nghĩa trên ta có:
2
-jβr
2 2
I β j 1
H = sin
θ + e a
4π βr β r
2
I sin
θ
H a
4πr
m
2
I sinθ
H = cos
ωt+ a
4πr
EE 2015 : Signals & Systems Tran Quang Viet – FEEE - HCMUT
Tran Quang Viet – FEEE – HCMUT Electromagnetics Field
Trường ĐT trong miền gần của nguyên tốanten thẳng
3
-jβr r
2 2 3 3
3
-jβr
θ
2 2 3 3
jI β j 1
E =- cosθ + e a
2πωε β r β r
jI β 1 j 1
- sin
θ - + + e a
4πωε βr β r β r
r
θ
3 3
jI cos
θ jI sinθ
E - a - a
2πωεr 4πωεr
mr
θ
3
I
E = sin(
ωt+ )(2cosθa +sinθa )
4πωεr
r
θ
3
-jI
= (2cos
θa +sinθa )
4πωεr
CuuDuongThanCong.com https://fb.com/tailieudientucntt