1
Tran Quang Viet – FEEE – HCMUT Electromagnetics Field
Trường điện từbiến thiên
Lecture 9
EE 2003: Trường điện từ
L.O.3.1 – Thiết lập hệ phương trình D’Alembert cho trường
điện từ biến thiên từ hệ phương trình Maxwell.
EE 2015 : Signals & Systems Tran Quang Viet – FEEE - HCMUT
Tran Quang Viet – FEEE – HCMUT Electromagnetics Field
Mô hình toán
Trường điện từbiến thiên là trường điện từcó các đại lượng
đặc trưng thay đổi theo không gian và thời gian, tuân thủ
theo các phương trình sau:
D
rotH = J + t
B
rotE = - t
V
divD =
divB = 0
V
divJ = -
t
1t 2t S
H - H = J
1t 2t
E - E = 0
1n 2n s
D - D =
s
1n 2n
J - J = -
t
D = E
B = H
J = E
CuuDuongThanCong.com https://fb.com/tailieudientucntt
2
EE 2015 : Signals & Systems Tran Quang Viet – FEEE - HCMUT
Tran Quang Viet – FEEE – HCMUT Electromagnetics Field
Định nghĩa thếvectơ& thếvô hướng
Định nghĩa thếvectơ:
divB = 0
div(rotA) = 0
B = rotA
Định nghĩa thếvô hướng:
B
rotE = - t
A
rot(E + ) = 0
t
rot(grad ) = 0
A
E = grad
t
Tính đa trịcủa các hàm thế:
( ) , )
A, (B E
( , , )
f
A+gradf ) (B E
t
Điều kiện phụLorentz: divA = -
t

EE 2015 : Signals & Systems Tran Quang Viet – FEEE - HCMUT
Tran Quang Viet – FEEE – HCMUT Electromagnetics Field
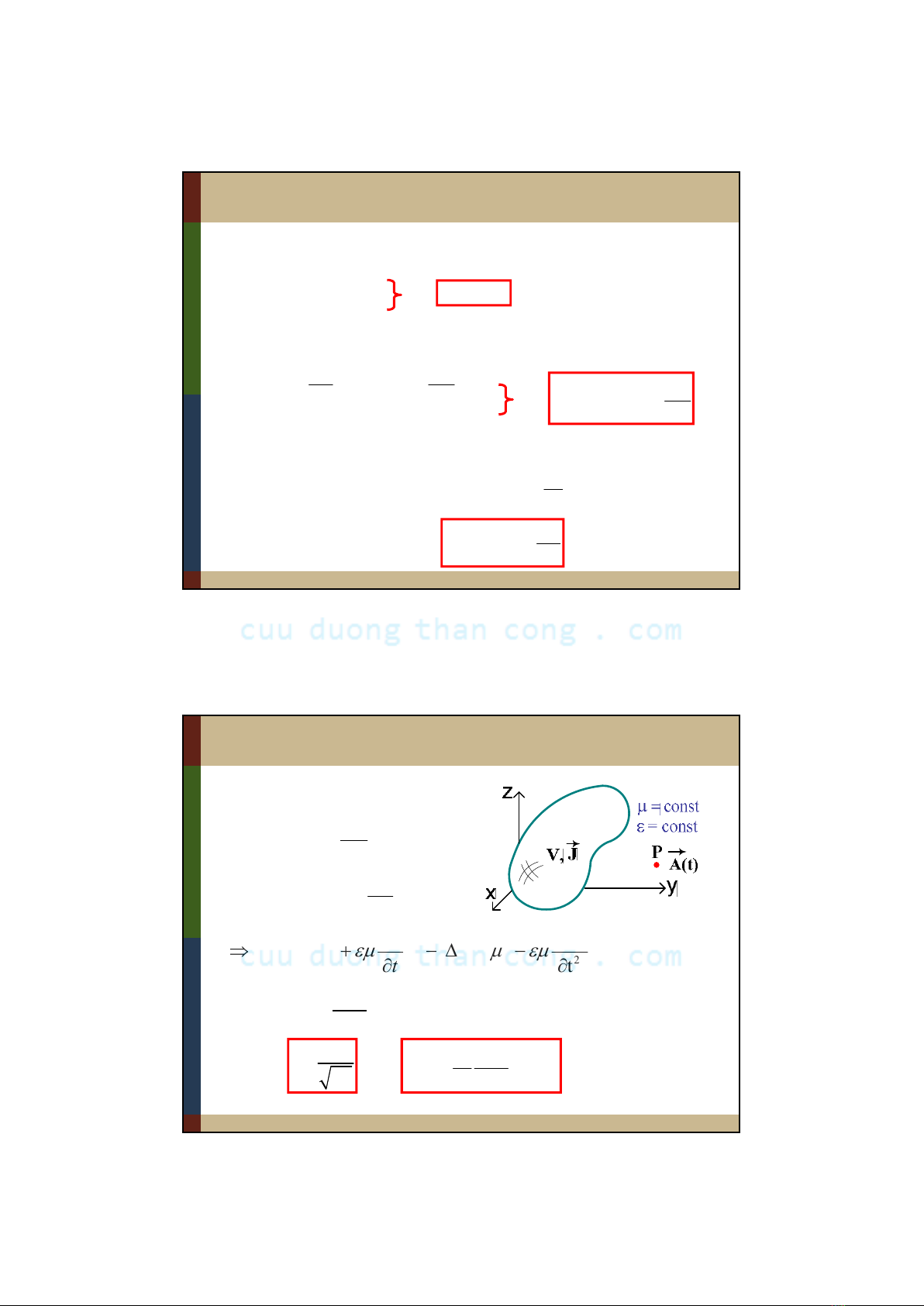
Phương trình d’Alembert cho thếvectơ
D
rotH = J
t
E
rotB = J
t

2
t

2
A
grad(divA ) A = J
t
2

2
A
A = J
t
2
2
1
v
2
A
A = J
t
1
v

Áp dụng pt Maxwell (1):
Đặt:
CuuDuongThanCong.com https://fb.com/tailieudientucntt
3
EE 2015 : Signals & Systems Tran Quang Viet – FEEE - HCMUT
Tran Quang Viet – FEEE – HCMUT Electromagnetics Field
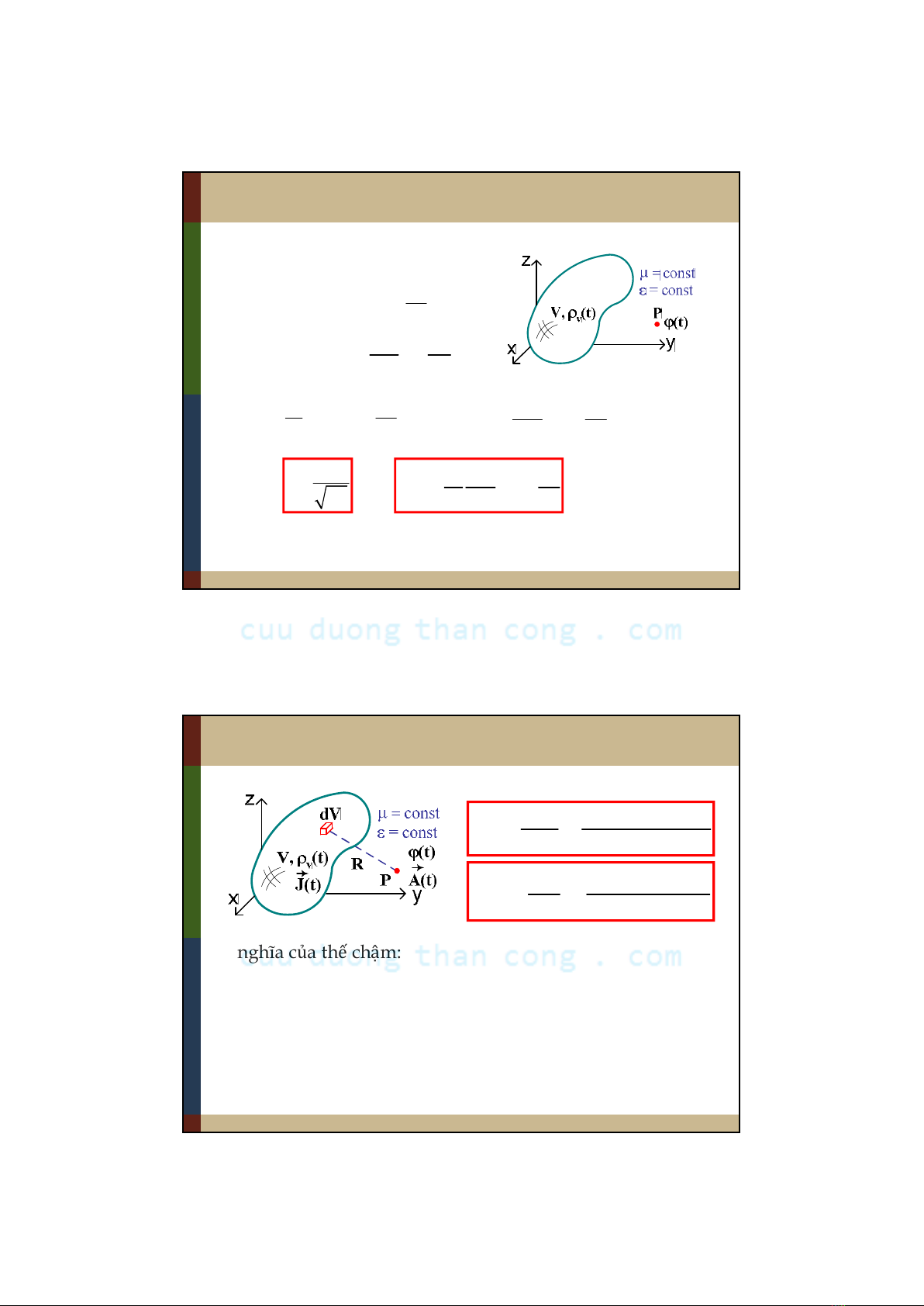
Phương trình d’Alembert cho thếvô hướng
divD = v
divE = v
v
A
div( grad ) =
t
divA=
t
v
2

v
2
=
t
2
2
1
v
v
2
=
t
1
v

Áp dụng pt Maxwell (3):
Đặt:
EE 2015 : Signals & Systems Tran Quang Viet – FEEE - HCMUT
Tran Quang Viet – FEEE – HCMUT Electromagnetics Field
Nghiệm phương trình d’Alembert – thếchậm
(t R/v)dV
1
(t)=
4 R
V
V

V
J(t R/v)dV
A(t)=
4 R
Ý nghĩa của thếchậm:
Trường điện từbiến thiên có khảnăng lan truyền trong
không gian dưới dạng sóng điện từ
Công cụtoán quan trọng đểtính trường điện từbức xạ
bởi anten
CuuDuongThanCong.com https://fb.com/tailieudientucntt
4
EE 2015 : Signals & Systems Tran Quang Viet – FEEE - HCMUT
Tran Quang Viet – FEEE – HCMUT Electromagnetics Field
Trường điện từbiến thiên điều hòa
Quy luật biến thiên theo thời gian của trường phụ thuộc vào
quy luật biến thiên của nguồn (mật độ điện tích và mật độ
dòng điện). Trong kỹ thuật ta thường gặp tín hiệu nguồn biến
thiên điều hòa, mặt khác một tín hiệu bất kỳ đều có thể biểu
diễn thành tổng các tín hiệu điều hòa dùng chuỗi Fourier (tín
hiệu tuần hoàn) hoặc tích phân Fourier (tín hiệu không tuần
hoàn) khảo sát trường điều hoàn là cơ bản và thực tế.
Một vectơ trường biến thiên điều hòa sẽ có dạng:
) ) )
x y z
xm x ym y zm z
X=X cos( t+ a +X cos( t+ a X cos( t+ a
xm xm ym ym zm zm
X =X (x,y,z);X =X (x,y,z);X =X (x,y,z)
x x y y z z
(x,y,z); (x,y,z); (x,y,z)
EE 2015 : Signals & Systems Tran Quang Viet – FEEE - HCMUT
Tran Quang Viet – FEEE – HCMUT Electromagnetics Field
Biểu diện phức trường biến thiên điều hòa
)
) )
y
x z
j( t+
j( t+ j( t+
x y z
xm ym zm
X=Re{X e }a +Re{X e }a Re{X e }a
)
) )
y
x z
j( t+
j( t+ j( t+
c
x y z
xm ym zm
X=Re{X e a +X e a +X e a }=Re{X }
)
) )
y
x z
j( t+
j( t+ j( t+
c
x y z
xm ym zm
X =X e a +X e a +X e a
j t
Xe
y
x z
j
j j
x y z
xm ym zm
X=X e a +X e a +X e a
X
c
X
X
Vectơ vật lý
(miền thời gian)
Vectơ biên độ
phức tức thời
Vectơ biên độ phức
(miền phức – tần số)
CuuDuongThanCong.com https://fb.com/tailieudientucntt
5
EE 2015 : Signals & Systems Tran Quang Viet – FEEE - HCMUT
Tran Quang Viet – FEEE – HCMUT Electromagnetics Field
Ví dụ:
2 2
2
5 ) 5 ) z
x x
y
E=3e cos( t x a 2e cos( t x a
2 2
5 ) 5 ) z
x x
y
E=3e cos( t x a 2e sin( t x a
6 ) 6 ) z
x
H 2sin( t y a +3cos( t y a
2
5 )
2 5 ) 2
z
E
j( t x
x j( t x x
c y
=3e e a 2e e a
2
2 5 2 5
]
z
E
j
x j x x j x j t
c y
=[3e e a 2e e e a e
2 5
]
z
E
x j x
y
=[3a +j2a e e
6
]
z
H
j y
x
=[j2a +3a e
2
6 )
6 6 )
]
c z z
H
j( t y+
j y j t j( t y
x x
=[j2a +3a e e 2e a +3e a
2
Re{ 6 ) 6 )
c z
H H
x
}=2cos( t y+ a +3cos( t y a
Biểu diện phức trường biến thiên điều hòa
EE 2015 : Signals & Systems Tran Quang Viet – FEEE - HCMUT
Tran Quang Viet – FEEE – HCMUT Electromagnetics Field
Hệphương trình Maxwell dạng phức
D
rotH J
t
E
rotH E
t
E
rot H E
t
C
C C
)
j t j t j t
rot(H E j E
e e e

( )rot H j E

Tương tự, ta có hệ phương trình Maxwell dạng phức:
( )rot H j E

rot E j H
/
divE
v
0divH
(1)
(2)
(3)
(4)
~
rot H j E
rot E j H
/
divE
v
0divH
(1)
(2)
(3)
(4)
Hoặc
~
( / )
j
: độ thẩm điện phức
CuuDuongThanCong.com https://fb.com/tailieudientucntt